目录
一、灰狼优化算法的python实现
二、灰狼优化算法与遗传算法的对比分析(python)
2.1 GWO1.py
2.2 GA1.py
2.3 GWO_vs_GA.py
2.4 运行结果
三、基于莱维飞行改进的灰狼优化算法的python实现
一、灰狼优化算法的python实现
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
'''定义函数'''
def function(X0):
'''
:param X0: x的取值
:param dim: 维度
:return: 函数值
'''
s=0
s=1/(1+np.abs(X0[0])+np.abs(X0[1])+np.abs(X0[2])+np.abs(X0[3]))
return s
'''灰狼优化算法——GWO'''
def GWO(NP,dim,NG,amax,x_max,x_min):
'''
:param NP:种群规模
:param dim: 数据维度
:param NG: 最大迭代步数
:param amax: 系数向量初始值
:param x_max: 解允许的最大值
:param x_min: 解允许的最小值
:return: 最优解的目标函数值
'''
'''随机产生初始解'''
X0=np.zeros((NP,dim))
value0=[] #函数值
for i in range(NP):
X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))
value0.append(function(X0[i]))
'''存储历史最优解和历史最优函数值'''
X_best=[] #历史最优解
value_best=[] #历史最优函数值
'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''
#得到对目标函数值列表value0升序排列后的索引
index_sort=np.argsort(np.array(value0))
#对value0进行降序排列
value0_sort=[value0[i] for i in index_sort[::-1]]
#对X0进行相应的排列
X0_sort=[X0[i] for i in index_sort[::-1]]
'''得到初始解的最优解和最优函数值'''
X_best.append(X0_sort[0])
value_best.append(value0_sort[0])
print("--------------------灰狼优化算法--------------------")
print("初始最优解:\n{}".format(X_best[0].tolist()))
print("初始最优函数值:\n{}".format(value_best[0]))
'''选出最优的三个个体,并获得它们的位置信息'''
Xalpha=X0_sort[0]
Xbeta=X0_sort[1]
Xdelta=X0_sort[2]
'''开始利用灰狼优化算法进行训练'''
for i in range(NG):
'''计算系数向量的参数a'''
ratio=i/NG
a=amax*(1-ratio)
'''对每个个体的位置进行更新'''
for j in range(NP):
'''分别计算在函数值最优的前三个个体的影响下,个体的位置移动量X1、X2、X3'''
C1=2*np.random.rand()
Dalpha=np.abs(C1*Xalpha-X0[j])
A1=2*a*np.random.rand()-a
X1=Xalpha-A1*Dalpha
C2=2*np.random.rand()
Dbeta=np.abs(C2*Xbeta-X0[j])
A2=2*a*np.random.rand()-a
X2=Xbeta-A2*Dbeta
C3=2*np.random.rand()
Ddelta=np.abs(C3*Xdelta-X0[j])
A3=2*a*np.random.rand()-a
X3=Xdelta-A3*Ddelta
'''计算个体移动后的位置及函数值'''
X0[j]=(X1+X2+X3)/3
value0[j]=function(X0[j])
'''对种群历史最优解和历史最优函数值进行更新'''
if max(value0)>max(value_best):
value_best.append(max(value0))
X_best.append(X0[value0.index(max(value0))])
else:
value_best.append(value_best[-1])
X_best.append(X_best[-1])
'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''
#得到对目标函数值列表value0升序排列后的索引
index_sort=np.argsort(np.array(value0))
#对X0进行相应的降序排列
X0_sort=[X0[i] for i in index_sort[::-1]]
'''选出最优的三个个体,并获得它们的位置信息'''
Xalpha=X0_sort[0]
Xbeta=X0_sort[1]
Xdelta=X0_sort[2]
'''返回最优解和最优函数值'''
return X_best,value_best
二、灰狼优化算法与遗传算法的对比分析(python)
2.1 GWO1.py
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
'''定义函数'''
def function(X0):
'''
:param X0: x的取值
:param dim: 维度
:return: 函数值
'''
s=0
s=1/(1+np.abs(X0[0])+np.abs(X0[1])+np.abs(X0[2])+np.abs(X0[3]))
return s
'''灰狼优化算法——GWO'''
def GWO(NP,dim,NG,amax,x_max,x_min):
'''
:param NP:种群规模
:param dim: 数据维度
:param NG: 最大迭代步数
:param amax: 系数向量初始值
:param x_max: 解允许的最大值
:param x_min: 解允许的最小值
:return: 最优解的目标函数值
'''
'''随机产生初始解'''
X0=np.zeros((NP,dim))
value0=[] #函数值
for i in range(NP):
X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))
value0.append(function(X0[i]))
'''存储历史最优解和历史最优函数值'''
X_best=[] #历史最优解
value_best=[] #历史最优函数值
'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''
#得到对目标函数值列表value0升序排列后的索引
index_sort=np.argsort(np.array(value0))
#对value0进行降序排列
value0_sort=[value0[i] for i in index_sort[::-1]]
#对X0进行相应的排列
X0_sort=[X0[i] for i in index_sort[::-1]]
'''得到初始解的最优解和最优函数值'''
X_best.append(X0_sort[0])
value_best.append(value0_sort[0])
print("--------------------灰狼优化算法--------------------")
print("初始最优解:\n{}".format(X_best[0].tolist()))
print("初始最优函数值:\n{}".format(value_best[0]))
'''选出最优的三个个体,并获得它们的位置信息'''
Xalpha=X0_sort[0]
Xbeta=X0_sort[1]
Xdelta=X0_sort[2]
'''开始利用灰狼优化算法进行训练'''
for i in range(NG):
'''计算系数向量的参数a'''
ratio=i/NG
a=amax*(1-ratio)
'''对每个个体的位置进行更新'''
for j in range(NP):
'''分别计算在函数值最优的前三个个体的影响下,个体的位置移动量X1、X2、X3'''
C1=2*np.random.rand()
Dalpha=np.abs(C1*Xalpha-X0[j])
A1=2*a*np.random.rand()-a
X1=Xalpha-A1*Dalpha
C2=2*np.random.rand()
Dbeta=np.abs(C2*Xbeta-X0[j])
A2=2*a*np.random.rand()-a
X2=Xbeta-A2*Dbeta
C3=2*np.random.rand()
Ddelta=np.abs(C3*Xdelta-X0[j])
A3=2*a*np.random.rand()-a
X3=Xdelta-A3*Ddelta
'''计算个体移动后的位置及函数值'''
X0[j]=(X1+X2+X3)/3
value0[j]=function(X0[j])
'''对种群历史最优解和历史最优函数值进行更新'''
if max(value0)>max(value_best):
value_best.append(max(value0))
X_best.append(X0[value0.index(max(value0))])
else:
value_best.append(value_best[-1])
X_best.append(X_best[-1])
'''对初始解的目标函数值进行降序排序,并一一对应得到相应的解'''
#得到对目标函数值列表value0升序排列后的索引
index_sort=np.argsort(np.array(value0))
#对X0进行相应的降序排列
X0_sort=[X0[i] for i in index_sort[::-1]]
'''选出最优的三个个体,并获得它们的位置信息'''
Xalpha=X0_sort[0]
Xbeta=X0_sort[1]
Xdelta=X0_sort[2]
'''返回最优解和最优函数值'''
return X_best,value_best
2.2 GA1.py
import random
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
'''产生初始种群'''
def initialpopulation(NP,n,x0,x1):
'''NP代表种群规模,n代表目标函数的未知量的个数;
x0代表未知数取值的下限,x1代表未知数取值的上限'''
initial=[]
for i in range(NP):
n_initial=[random.uniform(x0,x1) for j in range(n)]
initial.append(n_initial)
return initial
'''标定适值函数'''
def fitnessfunction(X):
'''X代表存储各个未知量的取值的列表'''
return 1/(math.sqrt(X[0]**2)+math.sqrt(X[1]**2)+math.sqrt(X[2]**2)+math.sqrt(X[3]**2)+1)
'''采用轮盘赌选择算法选择个体'''
def selection(NP,X0):
'''NP代表种群规模,X0代表种群'''
#计算种群中各个个体的适应值
value=[]
for i in range(NP):
value.append(fitnessfunction(X0[i]))
'''计算适应度和累计概率函数'''
#计算选择概率
fsum=0
for i in range(NP):
fsum=fsum+value[i]**2
value_ratio=[]
for i in range(NP):
value_ratio.append((value[i]**2)/fsum)
#计算累加概率
value_ratio_add=[]
for i in range(NP):
if i==0:
value_ratio_add.append(value_ratio[i])
else:
value_ratio_add.append(value_ratio_add[i-1]+value_ratio[i])
#产生[0,1]之间的随机数,进行NP次轮转
random_ratio=[random.uniform(0,1) for i in range(NP)]
#进行轮盘赌选择
choose_index=[] #从0开始计
value_ratio_add0=[0,*value_ratio_add] #在列表value_ratio_add的最前面加上一个0
for i in range(NP):
for j in range(NP):
if random_ratio[i]>=value_ratio_add0[j] and random_ratio[i]<value_ratio_add0[j+1]:
choose_index.append(j)
break
#得到经过轮盘赌选择算法后的种群
population=[X0[i] for i in choose_index]
return population
'''遗传运算——双切点交叉'''
def crossover1(X0,pc,NP,n):
'''X0代表种群,pc代表交叉概率,NP代表种群规模,n代表染色体上的基因数目'''
# 对每个染色体生成一个[0,1]之间的随机数
random_crossover=[random.uniform(0, 1) for i in range(NP)]
# 判断哪些染色体进行交叉运算
crossover_index=[] # 种群中进行交叉运算的染色体的索引值
for i in range(NP):
if random_crossover[i]<pc:
crossover_index.append(i)
# 判断初步确定的需要交叉的染色体个数,如果为奇数,则最后一个染色体不进行交叉运算
if (len(crossover_index)%2)!=0:
crossover_index.pop()
crossover_index=crossover_index
#进行双切点交叉
if len(crossover_index)!=0:
randint_index=[sorted(random.sample([i for i in range(0,n-1)],2)) for i in range(int(len(crossover_index)/2))]
for i in range(0,len(crossover_index),2):
crossover1=X0[crossover_index[i]]
crossover2=X0[crossover_index[i+1]]
crossoverindex=randint_index[int(i/2)]
#分割
crossover1_1=[crossover1[j] for j in range(crossoverindex[0]+1)]
crossover1_2=[crossover1[j] for j in range(crossoverindex[0]+1,crossoverindex[1]+1)]
crossover1_3=[crossover1[j] for j in range(crossoverindex[1]+1,n)]
crossover2_1=[crossover2[j] for j in range(crossoverindex[0]+1)]
crossover2_2=[crossover2[j] for j in range(crossoverindex[0]+1,crossoverindex[1]+1)]
crossover2_3=[crossover2[j] for j in range(crossoverindex[1]+1,n)]
#交换
X0[crossover_index[i]]=[*crossover1_1,*crossover2_2,*crossover1_3]
X0[crossover_index[i+1]]=[*crossover2_1,*crossover1_2,*crossover2_3]
#返回进行双切点交叉后的种群
return X0
'''进行遗传运算——变异'''
def mutation(X0,pm,NP,n,x0,x1):
'''X0代表种群,pm代表交叉概率,NP代表种群规模,n代表染色体上的基因数目
x0代表未知数取值的下限,x1代表未知数取值的上限'''
#生成在[0,1]上的随机数列表
random_gene=[[random.uniform(0,1) for i in range(n)] for j in range(NP)]
#进行变异运算
for i in range(NP):
for j in range(n):
if random_gene[i][j]<pm:
X0[i][j]=random.uniform(x0,x1)
#返回经过变异操作后的种群
return X0
'''计算种群中所有个体的适应值并返回最大值'''
def fitnessmax(X0,NP):
'''X0代表种群,NP代表种群规模'''
#计算种群中各个个体的适应值
value=[]
for i in range(NP):
value.append(fitnessfunction(X0[i]))
value_max=max(value)
#适应值最大所对应的索引值
index_max=value.index(max(value))
#适应值最大所对应的染色体
X0_max=X0[index_max]
return value_max,X0_max
'''使用双切点交叉的遗传算法'''
def GA1(NP,NG,n,x0,x1,pc,pm):
'''NP代表种群规模,NG代表最大代数,n代表一个染色体的基因数
x0代表未知数取值的下限,x1代表未知数取值的上限
pc代表交叉概率,pm代表变异概率'''
#遗传算法——单切点交叉
#print("----------------------------------------------------------遗传算法(双切点交叉)----------------------------------------------------------")
#产生初始种群
X0=initialpopulation(NP,n,x0,x1)
'''得到种群的最大适应值和对应的染色体'''
value_max, valueX0_max = fitnessmax(X0, NP)
print("--------------------遗传算法--------------------")
print("初始最优解:\n{}".format(valueX0_max))
print("初始最优函数值:\n{}".format(value_max))
#存储最大适应值和对应的函数值的列表
fitnessmax_list=[]
X0max_list=[]
#历史最大适应值
history_max=0
history=[]
history_X0=[]
for i in range(NG):
'''得到种群的最大适应值和对应的染色体'''
value_max,valueX0_max=fitnessmax(X0,NP)
fitnessmax_list.append(value_max)
X0max_list.append(valueX0_max)
if i==0:
history_max=value_max
history.append(history_max)
history_X0.append(valueX0_max)
else:
if value_max>=history_max:
history_max=value_max
history.append(history_max)
history_X0.append(valueX0_max)
else:
history.append(history_max)
history_X0.append(history_X0[i-1])
#print("第{}代:{} value_max={}".format(i + 1, history_X0[i], history[i]))
'''选择'''
X1=selection(NP,X0)
'''双切点交叉运算'''
X2=crossover1(X1,pc,NP,4)
'''变异运算'''
X3=mutation(X2,pm,NP,4,-10,10)
X0=X3
print("最优解Best={}".format(history[-1]))
#print("---------------------------------------------------------------进程结束---------------------------------------------------------------")
'''返回历代的最优函数值和最优解'''
return history,history_X02.3 GWO_vs_GA.py
import GWO1
import GA1
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
if __name__=="__main__":
'''得到遗传算法求解结果'''
#最大迭代步数
NG=1000
#种群规模
NP=100
#交叉率
pc=0.9
#变异率
pm=0.1
#染色体基因数
n=4
#未知数的下限
x0=-10
#未知数的上限
x1=10
#进行双切点交叉的遗传运算
historymax,historymaxX0=GA1.GA1(NP,NG,n,x0,x1,pc,pm)
print("最优解:\n{}".format(historymaxX0[-1]))
print("最优函数值:\n{}".format(historymax[-1]))
'''得到灰狼优化算法的求解结果'''
#最大迭代步数
NG=1000
#种群规模
NP=100
#数据维度
dim=4
#x允许的最大值和最小值
x_max=10
x_min=-10
#系数向量初始值
amax=2
'''灰狼优化算法'''
X_best,value_best=GWO1.GWO(NP,dim,NG-1,amax,x_max,x_min)
print("最优解:\n{}".format(X_best[-1]))
print("最优函数值:\n{}".format(value_best[-1]))
'''绘制遗传算法和灰狼优化算法的优化过程'''
plt.plot([int(i) for i in range(NG)],historymax,label="GA")
plt.plot([int(i) for i in range(NG)],value_best,label="GWO",c="red")
plt.title("遗传算法(GA)和灰狼优化算法(GWO)的优化过程")
plt.xlabel("代数")
plt.ylabel("函数值")
plt.grid()
plt.legend()
plt.show()
2.4 运行结果

 三、基于莱维飞行改进的灰狼优化算法的python实现
三、基于莱维飞行改进的灰狼优化算法的python实现
import numpy as np
import math
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
'''定义函数并求解函数值'''
def function(X0):
'''
:param X0:解向量
:return: 函数值
'''
s1=0
for i in range(len(X0)):
s1=s1+(X0[i])**2
s2=0
for i in range(len(X0)):
s2=s2+np.cos(2*(np.pi)*X0[i])
s=-20*np.exp(-0.2*(np.sqrt((1/len(X0))*s1)))-np.exp((1/len(X0))*s2)+20+np.e
return s
'''嵌入莱维飞行的灰狼优化算法'''
def LGWO(NP,dim,NG,amax,x_max,x_min):
'''
:param NP:种群规模
:param dim: 数据维度
:param NG: 最大迭代步数
:param amax: 系数向量初始值
:param x_max: 解允许的最大值
:param x_min: 解允许的最小值
:return: 最优解和最优解的目标函数值
'''
'''随机产生初始解'''
X0=np.zeros((NP,dim))
value0=[] #函数值
for i in range(NP):
X0[i]=np.random.uniform(low=x_min,high=x_max,size=(1, dim))
value0.append(function(X0[i]))
'''存储历史最优解和历史最优函数值'''
X_best=[] #历史最优解
value_best=[] #历史最优函数值
'''对初始解的目标函数值进行升序排序,并一一对应得到相应的解'''
#得到对目标函数值列表value0升序排列后的索引
index_sort=np.argsort(np.array(value0))
#对value0进行升序排列
value0_sort=[value0[i] for i in index_sort]
#对X0进行相应的排列
X0_sort=[X0[i] for i in index_sort]
'''得到初始解的最优解和最优函数值'''
X_best.append(X0_sort[0])
value_best.append(value0_sort[0])
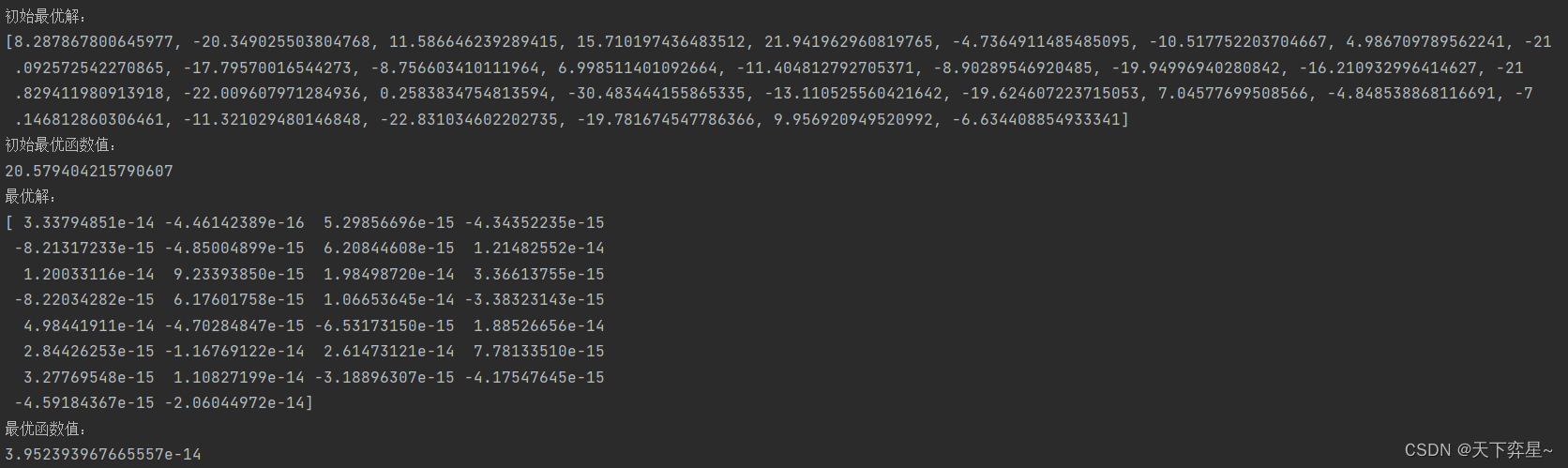
print("初始最优解:\n{}".format(X_best[0].tolist()))
print("初始最优函数值:\n{}".format(value_best[0]))
'''选出最优的两个个体,并获得它们的位置信息'''
Xalpha=X0_sort[0]
Xalpha_score=value0_sort[0]
Xbeta=X0_sort[1]
Xbeta_score=value0_sort[1]
'''进行嵌入莱维飞行的灰狼优化算法'''
for i in range(NG):
'''计算系数向量的参数a'''
ratio=i/NG
a=amax*(1-ratio)
for j in range(NP):
'''边界处理'''
for k in range(dim):
if X0[j][k]>x_max:
X0[j][k]=x_max
if X0[j][k]<x_min:
X0[j][k]=x_min
'''计算函数值'''
value=function(X0[j])
'''更新Alpha,Beta'''
if value<Xalpha_score:
Xalpha_score=value
Xalpha=X0[j]
elif value<Xbeta_score:
Xbeta_score=value
Xbeta=X0[j]
'''更新所有个体'''
Xbest=X0[0]
valuebest=function(X0[0])
for j in range(NP):
for k in range(dim):
r1=np.random.rand()
r2=np.random.rand()
A1=2*a*r1-a
C1=2*r2
D_alpha=np.abs(C1*Xalpha[k]-X0[j][k])
r1=np.random.rand()
r2=np.random.rand()
A2=2*a*r1-a
C2=2*r2
D_beta=np.abs(C2*Xbeta[k]-X0[j][k])
X0_old=X0[j]
A=np.random.rand()
if np.abs(A)<0.5:
X0[j][k]=0.5*(Xalpha[k]-A1*D_alpha+Xbeta[k]-A2*D_beta)
else:
beta=1.5 #beta一般取1.5
sigma_u=((math.gamma(1+beta)*math.sin(np.pi*beta/2))/(math.gamma((1+beta)/2)*beta*2**(0.5*(beta-1))))**(1/beta)
u=np.random.normal(0,sigma_u)
v=np.random.normal(0,1)
alpha_levi=(0.01*u*(X0[j][k]-Xalpha[k]))/(np.abs(v)**(-beta))
X0[j][k]=0.5*(Xalpha[k]-A1*D_alpha+Xbeta[k]-A2*D_alpha)+alpha_levi
'''贪婪选择算法'''
rnew=np.random.rand()
p=np.random.rand()
if function(X0[j])>function(X0_old) and rnew<p:
X0[j]=X0_old
'''计算函数值'''
value1=function(X0[j])
'''更新历史最优解和历史最优函数值'''
if value1<valuebest:
valuebest=value1
Xbest=X0[j]
if valuebest<value_best[-1]:
value_best.append(valuebest)
X_best.append(Xbest)
else:
value_best.append(value_best[-1])
X_best.append(X_best[-1])
'''绘制优化过程'''
plt.plot([int(i) for i in range(NG+1)],value_best)
plt.title("嵌入莱维飞行的灰狼优化算法(LGWO)的优化过程")
plt.xlabel("代数")
plt.ylabel("函数值")
plt.grid()
plt.show()
return X_best[-1],value_best[-1]
'''主函数'''
if __name__=="__main__":
'''最大迭代步数'''
NG=500
'''种群规模'''
NP=30
'''数据维度'''
dim=30
'''x允许的最大值和最小值'''
x_max=32
x_min=-32
'''系数向量初始值'''
amax=2
'''嵌入莱维飞行的灰狼优化算法'''
X_best,value_best=LGWO(NP,dim,NG,amax,x_max,x_min)
print("最优解:\n{}".format(X_best))
print("最优函数值:\n{}".format(value_best)) 






![[移动通讯]【Carrier Aggregation-10】【 Radio Resource Control (RRC) Aspects】](https://img-blog.csdnimg.cn/b28a0efd46c0463c97708459a299e8d8.png)
![Django3框架-(3)-[使用websocket]:使用channels实现websocket功能;简化的配置和实际使用方式](https://img-blog.csdnimg.cn/41e047b8c5844e0b8c2b71fb12a0fedf.png)