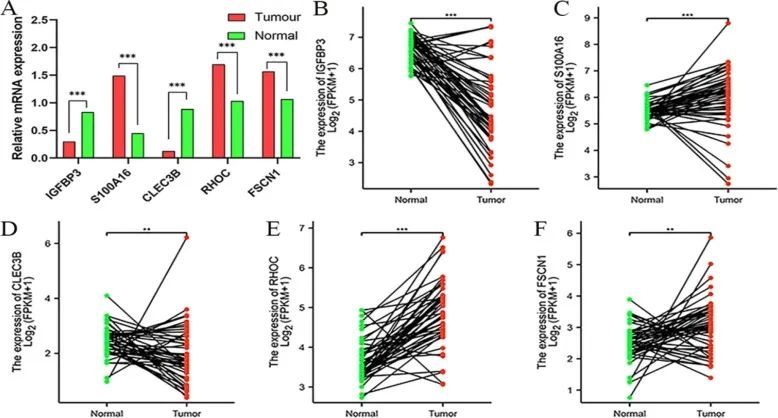
目录
什么是图信号?
如何理解图信号的”谱“?
图傅里叶变换是什么?
图傅里叶变换中特征值和图信号的总变差有什么关系?
让我们先总结一下,我们想要把图信号
正交分解到一组基
上;
那么
怎么得到?可以通过对图的拉普拉斯矩阵
做特征分解得到,即
.
于是


总变差:

是对角阵的第个特征值。
什么是图信号?
图信号定义:
给定图G=(V,E),V为节点集合,长度为N,图信号是一种描述V→R的映射,向量表示
![]()
每个x代表对应下标的节点上的信号强度。
与普通信号不同的是:图信号定义在节点上,节点存在固有的关联结构。
如何理解图信号的”谱“?
当我们在讨论图卷积神经网络时,”谱“意味着图拉普拉斯矩阵的特征分解。
假设 图信号 有 N个分量, 如果能找到一组正交基向量,我们就可以通过这组正交基向量的线性组合 来表达图信号。
用人话举个例子:
对于一个三维空间,一个向量
是三维的,我们用一组正交基
表示,假设
。
现在把图信号想象成
,我们要对这个图信号做正交分解,实际就是用一组正交基来表示图信号,在各个基上的强度就是那个变量 3 2 1,
就是
的线性组合。
在信号的傅里叶变换中,实际上也是把一个信号分解在了一组正交基上,这组正交基就是
现在对于图信号,我们也想做正交分解,假设这组正交基是
有了这组正交基,我们就可以定义图的傅里叶变换了。
图傅里叶变换是什么?
图的傅里叶变换就是一种数学变换。它将图的而拉普拉斯矩阵分解为特征值和特征向量。
图的拉普拉斯矩阵(L是拉普拉斯矩阵,D是度矩阵,A是邻接矩阵,这里不细讲)
在图的傅里叶变换中,拉普拉斯矩阵中的而特征值,也就是该矩阵的谱,(你可以理解为各个分量前对应的系数)特征向量(理解为那组正交的向量)。
对于某个图信号 而言,它的离散傅里叶变换同样可以记作 点积 的形式,即
其中表示图信号向量
的第i个分量,
是特征值
对应的特征向量,
表示第k个特征向量
的第i个分量。
表示图信号在第 k个傅里叶基上的投影,即所谓的傅里叶系数。这个投影的大小实际也衡量了图信号和这个基之间的相似度,也可以说,他是信号在某个基上的强度。
图傅里叶的逆变换表达:
从线性代数角度来看,构成一组完备的正交基向量,因此图上的任意信号都可以表达为这些基向量的线性组合,组合的系数(权重)就是 它在基向量上的投影(傅里叶系数
)。
图傅里叶变换中特征值和图信号的总变差有什么关系?
总变差(Total Variation)是一个标量,描述的是两个信号量两两之间的差值。
由表达式可知,总变差与特征值之间存在非常直接的线性关系,总变差是所有特征值的一个线性组合,其权重是图信号所对应的傅里叶系数的平方。总变差衡量图信号整体平滑度,可将特征值等价于频率,特征值越低,频率越低,相近节点信号趋于一致;频率越高,相近节点上信号差异越大。
例子
import numpy as np
np.set_printoptions(precision = 2, suppress = True)
A = np.array([
[0, 1, 1, 0, 0],
[1, 0, 1, 1, 0],
[1, 1, 0, 1, 0],
[0, 1, 1, 0, 1],
[0, 0, 0, 1, 0]],
)
A_sum = np.sum(A, axis = 0) #度数矩阵的按列求和
D = np.diag(A_sum) #求得度数矩阵
L = D - A #求得拉普拉斯矩阵
print(L) #输出拉普拉斯矩阵
(evals,evecs) = np.linalg.eig(L) #求拉普拉斯特征值及其向量
sorted_index = np.argsort(evals) #特征值降序
lambda_matrix = np.diag(evals[sorted_index]) #获取特征值对角阵
print(lambda_matrix)
sorted_vectors = evecs[:,sorted_index] #特征值对应的特征向量
print(sorted_vectors)Reference:
《从深度学习到图神经网络》 张玉宏、杨铁军著
图卷积网络原来是这么回事(一)——拉普拉斯矩阵初探 - 知乎 (zhihu.com)![]() https://zhuanlan.zhihu.com/p/290755442
https://zhuanlan.zhihu.com/p/290755442