139.单词拆分

题目

给一个非空字符串s，和一个非空单词集 wordDict，判断可不可以用空格把s分为wordDict里的一个或多个单词（必须全部拆成单词才返回ture）。

（可以重复拆分为单词集的同个单词，默认单词集没有重复的）

思路：

字符串s比作背包，单词比作物品，单词能否组成字符串s，就是问物品能不能把背包装满。

单词可以重复拆分（使用），表示是完全背包。

dp[i]含义：

dp[i]表示字符串长度为i的时候可以用空格拆分成单词集的一个或多个单词

递推公式：

dp[i]的状态可以由dp[j]（j<i）和 在 j - i 之间的字符串是否能被用空格拆分成单词集的一个或多个单词的状态推出来，如果dp[j]（j<i）为ture，同时 j - i 也为ture（能被拆分），那么可以推出dp[i]为ture。（这里满足条件就ture）

                string word = s.substr(j, i - j); //substr(起始位置，截取的个数)
                if (wordSet.find(word) != wordSet.end() && dp[j]) {
                    dp[i] = true;

初始化：

dp[0]=ture，dp[0]是推导的根基，如果dp[0]是false，那么两个条件判断就没法推导下去了，

dp[除了0之外的]都初始为false，如果满足条件了，会被覆盖成ture

遍历顺序:

求的是排列数，先背包后物品，比如字符串s是applepen，apple+pen和pen+apple，只有apple+pen 是符合的，只有apple+pen才能变成applepen

总代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;
        for (int i = 1; i <= s.size(); i++) {   // 遍历背包
            for (int j = 0; j < i; j++) {       // 遍历物品
                string word = s.substr(j, i - j); //substr(起始位置，截取的个数)
                if (wordSet.find(word) != wordSet.end() && dp[j]) {
                    dp[i] = true;
                }
            }
        }
        return dp[s.size()];
    }
};

多重背包理论

多重背包也是一种01背包，在01背包问题的基础上，每种物品有多件可以用，把多件同一物体摊开成多个物体就是多重背包。

多重背包： 

	重量	价值	数量
物品0	1	15	2
物品1	3	20	3
物品2	4	30	2

 摊开成01背包：

	重量	价值	数量
物品0	1	15	1
物品0	1	15	1
物品1	3	20	1
物品1	3	20	1
物品1	3	20	1
物品2	4	30	1
物品2	4	30	1

 代码按01背包写，在01背包的基础上“摊开”，插入多个同级物品或者直接加一层for循环遍历个数

代码这里，代码随想录

背包问题总结

01背包

物品只能放一次或者不放就是01背包。

递推公式：

问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

问装满背包有几种方法：dp[j] += dp[j - nums[i]];

问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); 

遍历顺序：

二维数组的01背包，先遍历物品或背包都可以，遍历顺序大到小，小到大遍历都可以

一维数组的01背包，只能先遍历物品再遍历背包，背包遍历需要从大到小。

完全背包

物品可以放无数个就是完全背包

遍历顺序：

纯完全背包问题，先遍历背包或物品都可以，同时第二层for循环必须由小到大

但是去区分，是求背包问题的组合还是排列数，组合先物品后背包，排列数先背包后物品。（同时第二层for循环需要从小到大）

如果求最小数无所谓物品背包的先后顺序

多重背包

01背包的物品加上个数就是多重背包，把01背包的代码，把个数变成对应的物品插入进去或者加一层for循环遍历就是多重背包的解决代码。

打家劫舍 I

题目：

给一个金额数组，元素值是正整数，每一个都可以被获取，但如果一个元素被获取了，那相邻的数组元素就不能被获取，求能获得的金额最大值

dp[i]含义：

dp[i]的意思就是，下标为i的数组能获取到的金额最大值dp[i]

递推公式：

dp[i]可以由偷不偷第i间房间的来，偷的话，dp[i]=dp[i-2]+num[i]，意为 i-1 间不偷，i-2间偷加上i间偷。另外一个就是i间不偷，考虑i-1间偷不偷。（会有偷了比不偷好的，比如1 1 1 1 100 1 1 1）

dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);(考虑下标i以及下标i之前能取到的最大值)

初始化：

由题目可知 dp[0]=num[0] ，dp[1]=max(num[0],num[1])

遍历顺序：

dp[i]由dp[i-2]和dp[i-1]推出来，所以由前向后遍历。

总代码

class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for (int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

打家劫舍 II

题目：

给一个环形的金额数组，首位是相互连接的，元素值是正整数，每一个都可以被获取，但如果一个元素被获取了，那相邻的数组元素就不能被获取，求能获得的金额最大值

思路：

因为首尾相连，数组头部尾部不能一起取，可以拆成3种可能的数组，考虑取头或取尾，或者考虑两个都不取，每一种可能的数组分离出来，由之前打劫1的代码去套，综合起来取最大值就好。

总代码：

这里考虑头尾都不取 被 考虑取头和考虑取尾的考虑范围覆盖了（包含头尾都不取的考虑范围）

// 注意注释中的情况二情况三，以及把198.打家劫舍的代码抽离出来了
class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2); // 考虑取头
        int result2 = robRange(nums, 1, nums.size() - 1); // 考虑取尾
        return max(result1, result2);
    }
    // 198.打家劫舍的逻辑
    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];
        vector<int> dp(nums.size());
        dp[start] = nums[start];//这里start是因为考虑数组
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};

打家劫舍 III

题目：

给一个二叉树，二叉树里面是金额的值（正整数），每一个节点的值都可以被获取，但是如果一个节点被获取了值，那它连接的其他节点不能被获取，求能获取金额的最大值。

思路：

用二叉树后续遍历，左右中，遍历左节点的同时遍历右节点，不断的求两个节点的可能最大值，然后到达根节点，继续判断取根据点大还是不取根节点大，然后对比最大值得出结果。

每个过程他是怎么求最大值的？

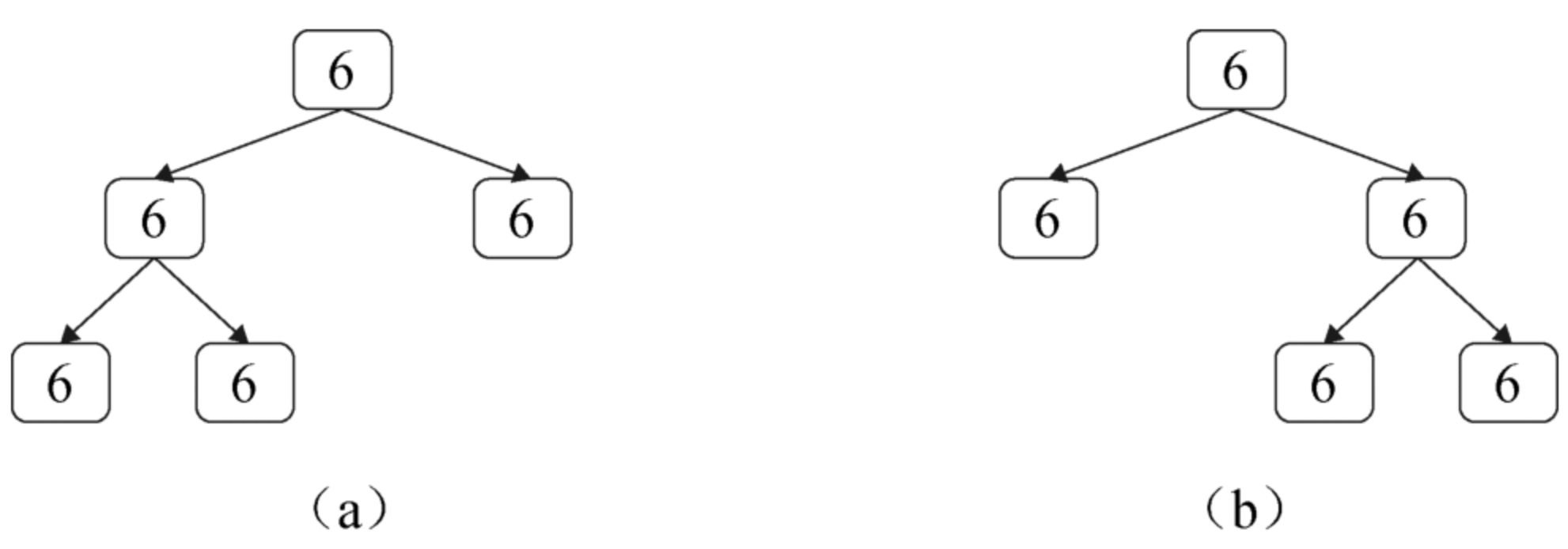
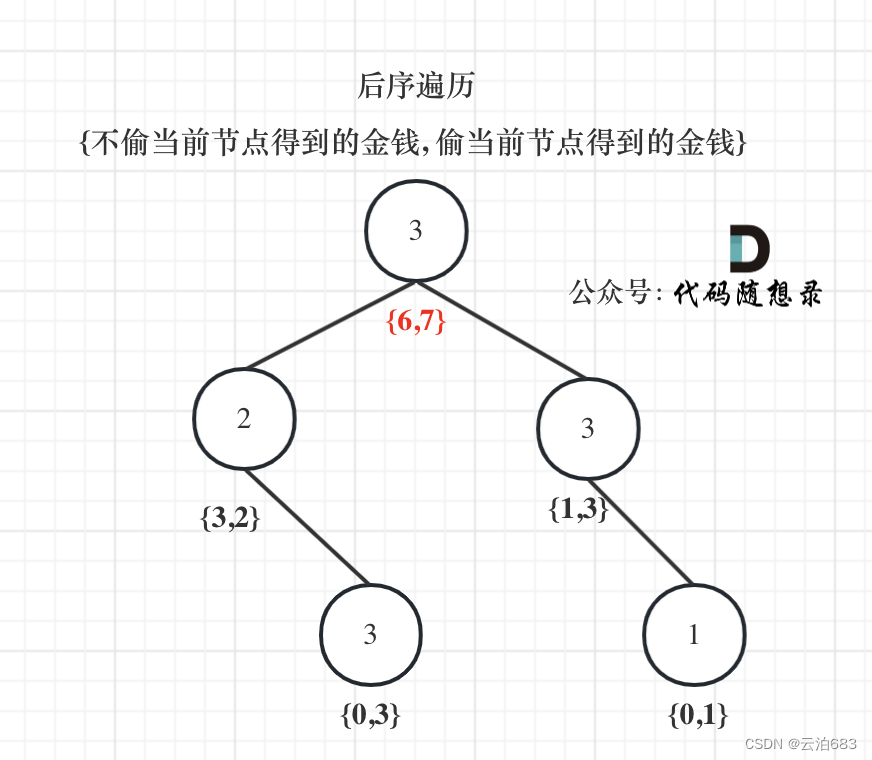
在后续遍历的基础上，用dp数组来代表偷和不偷得到的最大金额，每一次回溯都会向上传递这一层偷与不偷的最大值，到最后左节点偷的最大值，左节点不偷的最大值，右节点偷的最大值，右节点不偷的最大值都完成了，到了根节点再判断，偷根节点的值最大还是不偷根节点的值最大，比如示例{6，7}，

不偷，就是其左节点不偷的最大值3+其右节点不偷的最大值3 = 6

偷，就是根节点的值3+他左孩子的孩子节点的偷最大值3+他右​​​​​​​孩子的孩子节点的偷最大值1 = 7

然后对比取最大值得到最大金额。

dp数组（dp table）以及下标的含义：

下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

遍历示例图和讲解：空降16.20

总代码：

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* cur) {
        if (cur == NULL) return vector<int>{0, 0};
        vector<int> left = robTree(cur->left);
        vector<int> right = robTree(cur->right);
        // 偷cur，那么就不能偷左右节点。
        int val1 = cur->val + left[0] + right[0];
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};

nb