相关概念
离散数学中的数论相关概念和公式如下:
1.最大公约数(GCD):两个整数a和b的最大公约数是能够同时整除a和b的最大正整数,记作GCD(a, b)。
2.最小公倍数(LCM):两个整数a和b的最小公倍数是能够同时整除a和b的最小正整数,记作LCM(a, b)。
3.欧几里得算法(Euclidean algorithm):一种求最大公约数的算法,它基于这样一个事实:对于任意两个正整数a和b,有GCD(a,b) = GCD(b,a mod b)(其中mod表示取模运算),而且GCD(a, 0) = a。
4.素数(prime number):一个大于1的正整数,其正因子只有1和它本身,即只能被1和它本身整除。
5.素数定理(Prime number theorem):一个以n为上限的正整数中,素数的个数约为n/ln(n)。
6.费马小定理(Fermat's little theorem):如果p是素数,a是不是p的倍数的整数,则a^(p-1) ≡ 1 (mod p)。
7.欧拉定理(Euler's theorem):如果a和n是正整数且互质,则a^φ(n) ≡ 1 (mod n),其中φ(n)表示小于等于n且和n互质的正整数的个数。
8.欧拉函数(Euler's totient function):φ(n)表示小于等于n且和n互质的正整数的个数,例如φ(10) = 4,因为1, 3, 7, 9都和10互质。
9.扩展欧几里得算法(Extended Euclidean algorithm):一种求解ax + by = GCD(a,b)的一组整数解x和y的算法。
10.中国剩余定理(Chinese remainder theorem):一种求解同余方程组的算法,它可以方便地求解形如x ≡ a1 (mod m1), x ≡ a2 (mod m2),… , x ≡ ak (mod mk)的同余方程组。
11.欧拉降幂定理(Euler's reduced power theorem):如果a和n是正整数且互质,则对于任意的整数b,有a^b ≡ a^(b mod φ(n) + φ(n)) (mod n)。
1. (程序题)同余方程升级版
求关于 x的同余方程 ax≡c(mod b) 的最小正整数解。
Input
一行,包含两个正整数 a,b,c用一个空格隔开。
Output
一个正整数 x ,即最小正整数解。输入数据保证一定有解。
Sample Input
3 10 1
Sample Output
7
下面给出了ex_gcd函数:
void Ex_gcd(int a, int b, int &x, int &y,int &d)
{
if(b == 0)//递归出口
{x = 1;y = 0;d=a;return;}
Ex_gcd(b, a%b, x, y,d);
int t;
t=x;
x =y;
y = t-(a/b)*y;
}
d: 最大公约数;x是解
#include <iostream>
using namespace std;
void Ex_gcd(int a, int b, int &x, int &y, int &d)
{
// 求最大公约数和扩展欧几里德算法
if (b == 0) // 如果b等于0,说明a就是最大公约数,同时x=1,y=0
{
x = 1;
y = 0;
d = a;
return;
}
Ex_gcd(b, a % b, x, y, d); // 递归调用,求解最大公约数和x、y的值
int t = x; // 保存x的值
x = y; // 更新x的值为上一次递归中的y
y = t - (a / b) * y; // 更新y的值为上一次递归中的x减去(a/b)乘以上一次递归中的y
}
int main()
{
int a, b, c;
cin >> a >> b >> c;
int x, y, d;
Ex_gcd(a, b, x, y, d); // 求解最大公约数和x、y的值
int ans = (c / d) * x % (b / d); // 求解方程的解
if (ans < 0)
ans += b / d; // 如果ans小于0,加上b/d
/**
在求解方程的解时,可能会得到一个负数的解。根据数学的定义,对于模运算,负数的结果应该是在模数
的范围内的正数。所以,如果ans小于0,就需要加上b/d,使得ans变为一个在模数范围内的正数。这样
可以保证最终得到的解是正确的。
*/
cout << ans << endl;
return 0;
}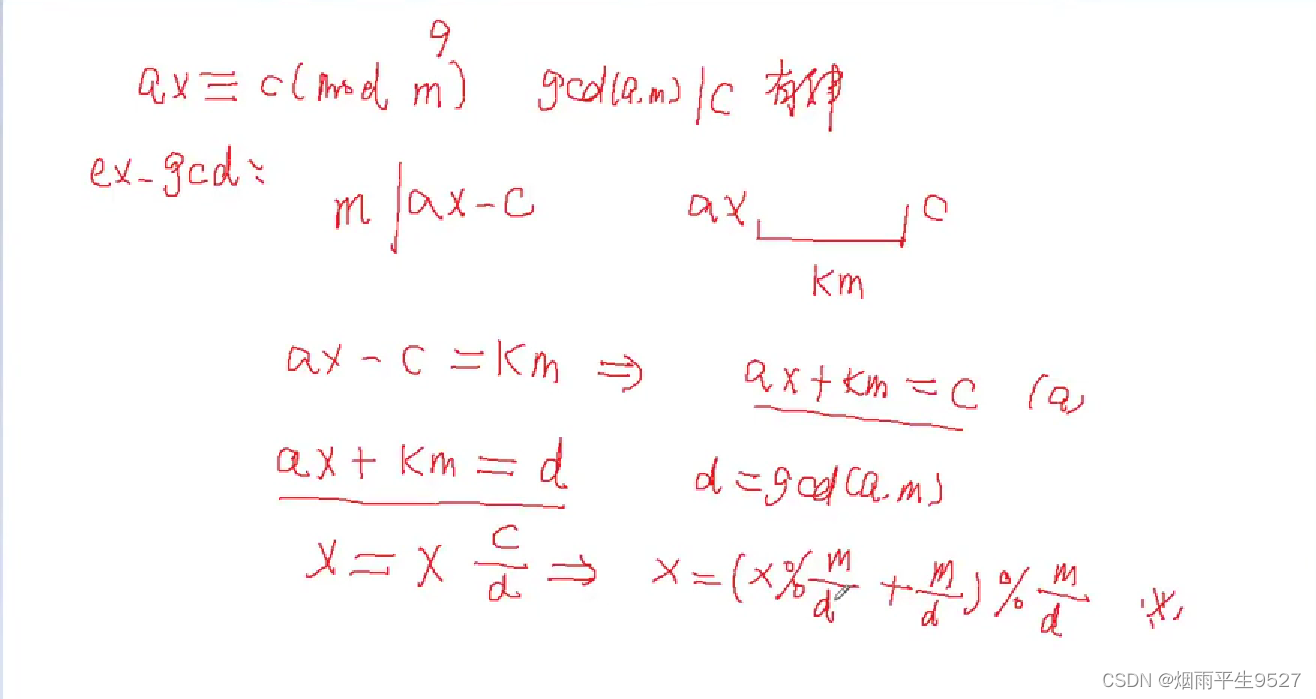
2. (程序题)高木同学的因子
今天西片同学又被高木同学捉弄了,高木同学跟西片同学玩了这么一个游戏。两人心中分别想一个数字,这两个数字分别为x和y(1<=x,y<=1e18),然后让西片同学说出一共有多少个整数既是x的因子,又是y的因子。由于西片和高木很有默契,所以保证他们两个想的数x和y的最大公因数不会超过1e9。这个问题又难住了西片同学了,你能帮帮西片同学告诉他答案吗?
Input
单组输入
数据占一行,包含两个整数x和y(1<=x,y<=1e18),保证gcd(x,y)<=1e9。
Output
输出既是x因子又是y因子的整数的个数。输出占一行
Sample Input
12 36
Sample Output
6
Hint
12和36有共同因子1 2 3 4 6 12共计6个数字,所以答案为6
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {
// 求最大公约数的函数
if (b == 0) {
return a; // 如果b等于0,返回a作为最大公约数
}
return gcd(b, a % b); // 递归调用,求解最大公约数
}
int main() {
ll x, y;
cin >> x >> y;
ll data = gcd(x, y); // 求解x和y的最大公约数
ll count = 0; // 初始化计数器为0
for (ll i = 1; i * i <= data; i++) {
// 从1开始遍历到data,每次增加1
// 如果i的平方小于等于data,则继续循环
// 否则跳出循环
if (data % i == 0) {
// 如果data能被i整除,说明i和data/i都是data的因数
// 因此计数器增加2
count += 2;
}
}
if ((ll)(sqrt(data)) * (ll)(sqrt(data)) == data) {
// 如果data的平方根的平方等于data,说明data是一个完全平方数
// 也就是说data有一个因数只出现一次,因此计数器减去1
count--;
}
cout << count << endl;
return 0;
}3. (程序题)费马小定理
给定3个正整数a,b,c,求a^(b^c) % 1000000007 (10^9 + 7)的值。
Input
多组输入,每组第一行3个数a,b,c,数据范围都在10^9以内。
Output
输出结果。
Sample Input
2 2 3
5 5 6
Sample Output
256
516190328
---------------------------------------------------------
typedef long long ll;
const int mod=1e9+7;
ll quick_mod(ll a,ll b,ll c)
{
ll ans=1;
while(b){
if(b&1){
ans=ans*a%c;
b--;
}
b>>=1;
a=a*a%c;
}
return ans;
}

#include <iostream>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
ll quick_mod(ll a, ll b, ll c)
{
ll ans = 1; // 初始化ans为1,表示初始结果为1
while (b) // 当指数b不为0时,进行循环
{
if (b & 1) // 如果b的最低位为1
{
ans = ans * a % c; // 将ans乘以a并取模c,得到新的ans
b--; // 将b减1
}
b >>= 1; // 将b右移1位,相当于将b除以2
a = a * a % c; // 将a平方并取模c,得到新的a
}
return ans; // 返回计算结果ans
}
int main()
{
ll a, b, c;
while (cin >> a >> b >> c)
{
ll ans = quick_mod(a, quick_mod(b, c, mod - 1), mod);
cout << ans << endl;
}
return 0;
}
上述代码实现了计算a^(b^c) % mod的功能,并结合费马小定理进行了优化。
- 首先,定义了一个长整型别名ll,用于表示较大的整数。
- 然后,定义了一个常量mod,表示取模的值,即对10^9 + 7取模。
- 接着,定义了一个函数quick_mod,用于快速计算幂的结果。
- 在主函数中,通过循环读入a、b、c的值,并调用quick_mod函数计算a^(b^c) % mod的结果,并输出结果。
费马小定理的优化主要体现在对指数b^c的计算上。根据费马小定理,a^(p-1) ≡ 1 (mod p),其中p为质数。因此,对于指数b^c,可以通过对mod-1取模,将指数缩小到mod-1的范围内,从而加快计算速度。在代码中,调用quick_mod函数时,将b^c对mod-1取模,得到新的指数,然后再计算a的该指数次幂。这样可以避免对较大的指数进行计算,提高了算法的效率。