Pmdarima实现单变量时序预测与交叉验证

news2024/11/19 19:18:51

目录

1. pmdarima实现单变量时间序列预测

2. 时间序列交叉验证

2.1 滚动交叉验证(RollingForecastCV)

2.2 滑窗交叉验证(SildingWindowForecastCV)

1. pmdarima实现单变量时间序列预测

        Pmdarima是以statsmodel和autoarima为基础、封装研发出的Python时序分析库、也是现在市面上封装程度最高、代码最为简洁的时序预测库之一。Pmdarima由sklearn团队开发，沿袭了sklearn库的代码习惯、并保留了一切接入sklearn的接口，是非常方便机器学习学习者学习的工具。该库包括了以R语言为基础的autoarima所有的功能，并且能够处理平稳性、季节性、周期性等问题，可以执行差分、交叉验证等运算，以及内容丰富的官方说明文档。以下是使用Pmdarima实现一个简单预测的过程：

import pmdarima as pm
from pmdarima import model_selection
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
import warnings
warnings.filterwarnings("ignore")

data = pm.datasets.load_wineind()
len(data) #176

fig=plt.figure(figsize=(16,5))
plt.plot(range(data.shape[0]),data)
plt.grid()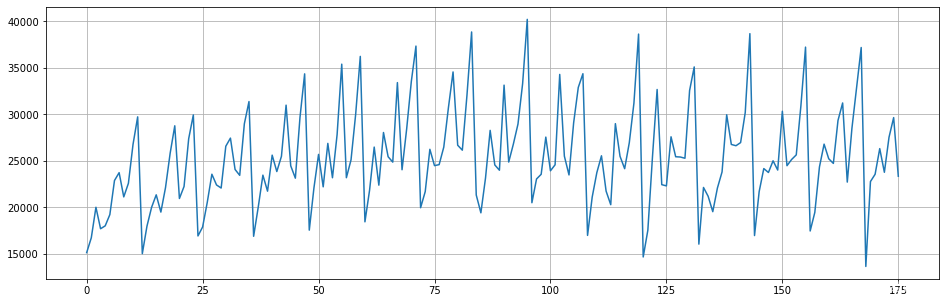

#使用pm分割数据，遵循时序规则，不会打乱时间顺序
train, test = model_selection.train_test_split(data, train_size=152)
#自动化建模，只支持SARIMAX混合模型,不支持VARMAX系列模型
arima = pm.auto_arima(train, trace=True, #训练数据，是否打印训练过程？
                      error_action='ignore', suppress_warnings=True, #无视警告和错误
                      maxiter=5, #允许的最大迭代次数
                      seasonal=True, m=12 #是否使用季节性因子？如果使用的话，多步预测的步数是多少？
                     )
Performing stepwise search to minimize aic
 ARIMA(2,1,2)(1,0,1)[12] intercept   : AIC=2955.247, Time=0.46 sec
 ARIMA(0,1,0)(0,0,0)[12] intercept   : AIC=3090.160, Time=0.02 sec
 ARIMA(1,1,0)(1,0,0)[12] intercept   : AIC=2993.480, Time=0.08 sec
 ARIMA(0,1,1)(0,0,1)[12] intercept   : AIC=2985.395, Time=0.09 sec
 ARIMA(0,1,0)(0,0,0)[12]             : AIC=3088.177, Time=0.02 sec
 ARIMA(2,1,2)(0,0,1)[12] intercept   : AIC=2978.426, Time=0.16 sec
 ARIMA(2,1,2)(1,0,0)[12] intercept   : AIC=2954.744, Time=0.18 sec
 ARIMA(2,1,2)(0,0,0)[12] intercept   : AIC=3025.510, Time=0.10 sec
 ARIMA(2,1,2)(2,0,0)[12] intercept   : AIC=2954.236, Time=0.49 sec
 ARIMA(2,1,2)(2,0,1)[12] intercept   : AIC=2958.264, Time=0.49 sec
 ARIMA(1,1,2)(2,0,0)[12] intercept   : AIC=2964.588, Time=0.38 sec
 ARIMA(2,1,1)(2,0,0)[12] intercept   : AIC=2950.034, Time=0.53 sec
 ARIMA(2,1,1)(1,0,0)[12] intercept   : AIC=2950.338, Time=0.24 sec
 ARIMA(2,1,1)(2,0,1)[12] intercept   : AIC=2953.291, Time=0.45 sec
 ARIMA(2,1,1)(1,0,1)[12] intercept   : AIC=2951.569, Time=0.21 sec
 ARIMA(1,1,1)(2,0,0)[12] intercept   : AIC=2958.953, Time=0.32 sec
 ARIMA(2,1,0)(2,0,0)[12] intercept   : AIC=2966.286, Time=0.35 sec
 ARIMA(3,1,1)(2,0,0)[12] intercept   : AIC=2951.433, Time=0.50 sec
 ARIMA(1,1,0)(2,0,0)[12] intercept   : AIC=2993.310, Time=0.39 sec
 ARIMA(3,1,0)(2,0,0)[12] intercept   : AIC=2952.990, Time=0.47 sec
 ARIMA(3,1,2)(2,0,0)[12] intercept   : AIC=2953.842, Time=0.58 sec
 ARIMA(2,1,1)(2,0,0)[12]             : AIC=2946.471, Time=0.45 sec
 ARIMA(2,1,1)(1,0,0)[12]             : AIC=2947.171, Time=0.17 sec
 ARIMA(2,1,1)(2,0,1)[12]             : AIC=2948.216, Time=0.42 sec
 ARIMA(2,1,1)(1,0,1)[12]             : AIC=2946.151, Time=0.29 sec
 ARIMA(2,1,1)(0,0,1)[12]             : AIC=2971.736, Time=0.14 sec
 ARIMA(2,1,1)(1,0,2)[12]             : AIC=2948.085, Time=0.50 sec
 ARIMA(2,1,1)(0,0,0)[12]             : AIC=3019.258, Time=0.06 sec
 ARIMA(2,1,1)(0,0,2)[12]             : AIC=2959.185, Time=0.36 sec
 ARIMA(2,1,1)(2,0,2)[12]             : AIC=2950.098, Time=0.52 sec
 ARIMA(1,1,1)(1,0,1)[12]             : AIC=2953.184, Time=0.14 sec
 ARIMA(2,1,0)(1,0,1)[12]             : AIC=2964.069, Time=0.14 sec
 ARIMA(3,1,1)(1,0,1)[12]             : AIC=2949.076, Time=0.16 sec
 ARIMA(2,1,2)(1,0,1)[12]             : AIC=2951.826, Time=0.16 sec
 ARIMA(1,1,0)(1,0,1)[12]             : AIC=2991.086, Time=0.09 sec
 ARIMA(1,1,2)(1,0,1)[12]             : AIC=2960.917, Time=0.14 sec
 ARIMA(3,1,0)(1,0,1)[12]             : AIC=2950.719, Time=0.13 sec
 ARIMA(3,1,2)(1,0,1)[12]             : AIC=2952.019, Time=0.17 sec

Best model:  ARIMA(2,1,1)(1,0,1)[12]          
Total fit time: 11.698 seconds
#预测
preds = arima.predict(n_periods=test.shape[0])
preds #按照测试集的日期进行预测
array([25809.09822027, 27111.50500611, 30145.84346715, 35069.09860267,
       19044.09098919, 22734.07766136, 24370.14476344, 24468.4989244 ,
       24661.71940304, 24465.6250753 , 29285.02123954, 25607.32326197,
       26131.79439226, 26937.20321329, 29632.82588046, 33904.51565498,
       20207.31393733, 23342.10936251, 24741.41755828, 24828.6385991 ,
       24993.22466868, 24825.14042152, 28939.23990247, 25799.92370898])
fig=plt.figure(figsize=(16,5))
plt.plot(range(test.shape[0]),test)
plt.plot(range(test.shape[0]),preds)
plt.grid()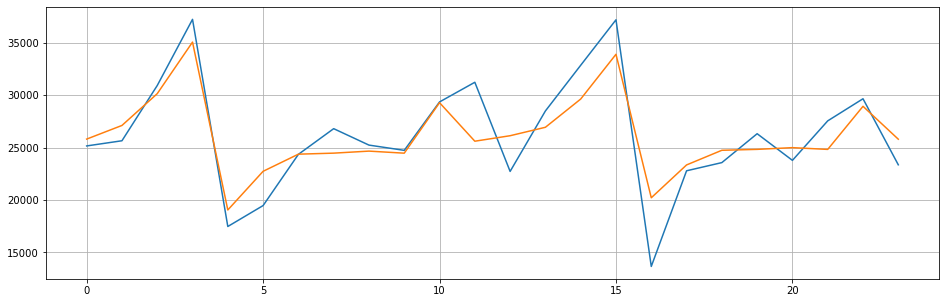

模型评估指标可共有sklearn的评估指标，也可调用特定的时序指标AIC：

np.sqrt(mean_squared_error(test, preds))
2550.8826581401277
arima.aic()
2946.1506587436375
arima.summary()

枚举式搜索合适的参数，从效率角度来说远远超过statsmodel，遗憾的是，从上述代码不难看出pmdarima的代码思路是更最近机器学习而不是统计学的，因此pmd.auto arima跑出的结果往往无法满足统计学上的各类检验要求，因此泛化能力无法被保证。同时也很容易发现，由于数据集分割的缘故，autoarima选择出的最佳模型可能无法被复现，例如我们使用autoarima选择出的最佳模型建立单模:

model=pm.ARIMA(order=(2,1,1),seasonal_order=(1,0,1,12),max_iter=500)
model.fit(train)

fig=plt.figure(figsize=(16,5))
plt.plot(range(test.shape[0]),test)
plt.plot(range(test.shape[0]),model.predict(n_periods=test.shape[0]))
plt.grid()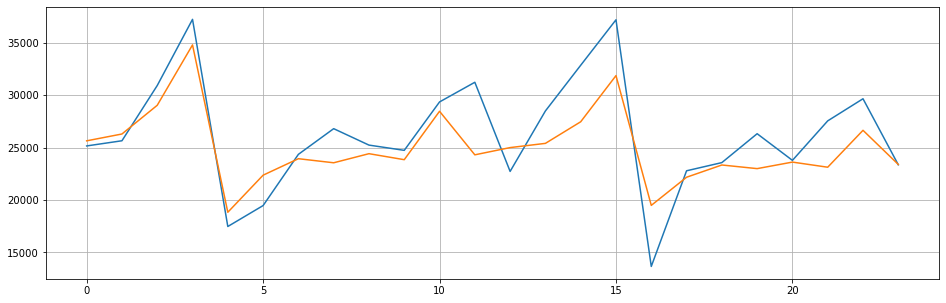

np.sqrt(mean_squared_error(test, model.predict(n_periods=test.shape[0])))
3081.3401428137163
model.aic()
2936.648256262213

        既然pmdarima是基于statsmodel搭建，也能够使用基于R语言的autoarima所有的功能，pmdarima自然也能够支持相应的各类统计学检验以及相关系数计算，更多的详情都可以参考pmdarima的官方说明文档。一般在使用pmdarima建模后，还需要使用统计学中的一系列检验来选择模型、找出能够通过所有检验的模型。

2. 时间序列交叉验证

        在时序模型的选择过程中，可以借助交叉验证来帮助我们选择更好的模型。时间序列的交叉验证非常特殊，因为时间序列数据必须遵守“过去预测未来”、“训练中时间顺序不能打乱"等基本原则，因此传统机器学习中的k折交叉验证无法使用。
        在时间序列的世界中，有以下两种常见的交叉验证方式：滚动交叉验证(RollingForecastCV) 和滑窗交叉验证 (SlidingWindowForecastCV)，当提到“时序交叉验证”时，一般特指滚动交叉验证。下面具体来看一下两种交叉验证的操作：

2.1 滚动交叉验证(RollingForecastCV)

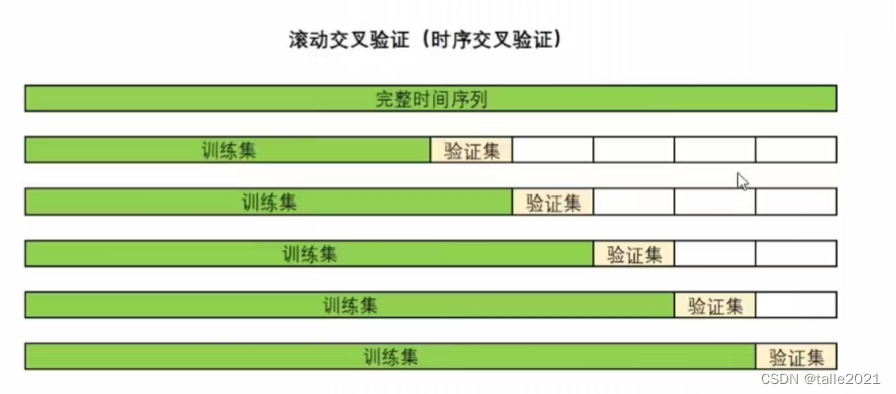
        滚动交叉验证是在验证过程中不断增加训练集、并让验证集越来越靠近未来的验证方式，这一方式既能保证我们一定是在用“过去预测未来”，同时也能够保证需要预测的未来和过去真实标签之间的是足够近的，因为越靠近未来的数据对未来的影响越大。这一交叉验证方式很像“多步预测”，但是该方式却不会存在多步预测中的“错误累计"问题，因为在训练过程中我们一直是在使用客观存在的真实标签。
        在pmdarima中，我们使用类 RollingForecastCV和 cross_validate 来实现交叉验证，很明显pmdarima的思路借鉴了sklearn (事实上，pmdarima在所有统计学相关内容上是借鉴并依赖于statsmodel进行运行，在所有机器学习相关内容上是借鉴sklearn进行运行)。sklearn中的交叉验证：

cv = KFold(n_splits=5,shuffle=True,random_state=1412)
results = cross_validate(reg,Xtrain,Ytrain,cv=cv)

其中cv是交叉验证具体的模式，cross_validate则负责执行交叉验证本身。在pmdarima运行交叉验证时，类RollingForecastCV的地位等同于普通机器学习交叉验证中的 KFold 类。RollingForecastCv 也只能规定交叉验证的模式，不负责执行交叉验证本身。特别的是，普通K折交叉验证是由折数来控制的，但时序交叉验证其实是以单个样本为单位的。一般来说，时序交叉验证的验证集可以是多个时间点，也可以为单个时间点。当验证集为1个时间点时，滚动交叉验证如下所示:

在pmdarima当中，使用RollingForecastCV来完成交叉验证：

class pmdarima.model selection.RollingForecastCV(h=1，step=1，initial=None)

h：验证集中的样本数量，可以输入[1,n_samples]的整数。
step：训练集中每次增加的样本数量，必须为大于等于1的正整数。
initial：第一次交叉验证时的训练集样本量，如果不填写则按1/3处理。

 取h=1,step=1,initial=10

data = pm.datasets.load_wineind()
cv=model_selection.RollingForecastCV(h=1,step=1,initial=10)
cv_generator=cv.split(data)
next(cv_generator)#根据initial初始训练集有10个样本，验证集遵循参数h的设置，只包含一个样本
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([10]))
next(cv_generator)#根据step的设置，训练集每次增加1个样本，验证集继续包含一个样本
(array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10]), array([11]))
next(cv_generator)
(array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11]), array([12]))

取h=10,step=5,initial=10

cv=model_selection.RollingForecastCV(h=10,step=5,initial=10)
cv_generator=cv.split(data)
next(cv_generator)
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
 array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19]))
next(cv_generator)
(array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14]),
 array([15, 16, 17, 18, 19, 20, 21, 22, 23, 24]))
next(cv_generator)
(array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
        17, 18, 19]),
 array([20, 21, 22, 23, 24, 25, 26, 27, 28, 29]))

不难发现，在pmdarima中实现滚动交叉验证时，验证集实际上是可以重复的，因此滚动交叉验证可以在有限的数据上进行多轮验证集重合的交叉验证，只要满足“过去预测未来”的基本条例，时序交叉验证其实可以相对自由的进行(即验证集与验证集之间不是互斥的)。也因此，时序交叉验证的实际运行时间往往会很长，当数据量巨大时交叉验证的负担也会更大。

# 沿用上面的数据和模型
model=pm.ARIMA(order=(2,1,1),seasonal_order=(1,0,1,12),max_iter=500)
cv=model_selection.RollingForecastCV(h=24,step=12,initial=36)
predictions=model_selection.cross_validate(model,data,cv=cv
                                            ,scoring="mean_squared_error"
                                            ,verbose=2
                                            ,error_score="raise")
[CV] fold=0 ..........................................................
[CV] fold=1 ..........................................................
[CV] fold=2 ..........................................................
[CV] fold=3 ..........................................................
[CV] fold=4 ..........................................................
[CV] fold=5 ..........................................................
[CV] fold=6 ..........................................................
[CV] fold=7 ..........................................................
[CV] fold=8 ..........................................................
[CV] fold=9 ..........................................................
predictions
{'test_score': array([1.35362847e+08, 1.08110482e+08, 2.18376249e+07, 1.97805181e+07,
        6.16138893e+07, 1.42418110e+07, 1.32432958e+07, 1.31182597e+07,
        3.57071218e+07, 5.79654872e+06]),
 'fit_time': array([0.2784729 , 0.12543654, 0.62335014, 0.64258695, 0.75659704,
        0.73791075, 0.82430649, 0.92007995, 0.98767185, 1.03166628]),
 'score_time': array([0.01047397, 0.        , 0.00223732, 0.        , 0.        ,
        0.        , 0.01564431, 0.        , 0.01562428, 0.01562572])}
np.sqrt(predictions["test_score"])
array([11634.55400113, 10397.61906654,  4673.07446159,  4447.52944078,
        7849.45153132,  3773.83240719,  3639.13393689,  3621.91381986,
        5975.54363899,  2407.60227639])

可以看到，交叉验证的测试集中得到的RMSE大部分都大于之前自动化建模时得到的RMSE(2550)，并且训练数据越少时，测试集上的RMSE会越大，这可能说明在前几折交叉验证时，训练集的数据量太少，因此可以考虑增大initial当中的设置来避免这个问题。

2.2 滑窗交叉验证(SildingWindowForecastCV)

        滑窗交叉验证是借助滑窗技巧完成的交叉验证。滑窗是时间序列中常见的技巧，具体操作如下:

Sliding window——>——>

在时间序列预测时，常常使用窗内的样本作为训练样本、窗右侧(或下方)的第一个样本做为被预测的样本。滑窗技巧在时间序列的各个领域都应用广泛，是时间序列的基础之一。很显然，滑窗交叉验证就是使用窗内的样本作为训练集，窗右侧(或下方)的样本作为验证集而进行的交叉验证。

与滚动交叉验证一样，滑窗交叉验证中的验证集也可以是单一样本，也可以是一系列数据集。相比起滚动交叉验证，滑窗交叉验证的优势在于训练集不会越来越大、每次训练时都使用了理论上对当前验证集来说最有效的信息。但同时，这个优势也会带来问题，由于训练集往往较小，因此滑窗交叉验证需要进行的建模次数异常地多，这可能导致交叉验证模型变得非常缓慢。

在pmdarima当中，使用 SlidingWindowForecastCV 来完成滑窗交叉验证
class pmdarima.model_selection.SlidingWindowForecastCV(h=1,step=1,window size=None)

h：验证集中的样本数量，可以输入[1,n_samples]的整数
step：每次向未来滑窗的样本数量，必须为大于等于1的正整数
window_size：滑窗的尺寸大小，如果填写None则按照样本量整除5得到的数来决定

取h=1,step=1,window_size=10

cv=model_selection.SlidingWindowForecastCV(h=1,step=1,window_size=10)
cv_generator=cv.split(data)
next(cv_generator)#首次进行交叉验证时的数据分割情况
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([10]))
next(cv_generator)#第二次交叉验证时的数据分割情况
(array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10]), array([11]))

 取h=10,step=5,window_size=10

cv=model_selection.SlidingWindowForecastCV(h=10,step=5,window_size=10)
cv_generator=cv.split(data)
next(cv_generator)
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
 array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19]))
next(cv_generator)
(array([ 5,  6,  7,  8,  9, 10, 11, 12, 13, 14]),
 array([15, 16, 17, 18, 19, 20, 21, 22, 23, 24]))
# 沿用上面的数据和模型
model=pm.ARIMA(order=(2,1,1),seasonal_order=(1,0,1,12),max_iter=500)
cv=model_selection.SlidingWindowForecastCV(h=24,step=12,window_size=36)
predictions=model_selection.cross_validate(model,data,cv=cv
                                            ,scoring="mean_squared_error"
                                            ,verbose=2
                                            ,error_score="raise")
[CV] fold=0 ..........................................................
[CV] fold=1 ..........................................................
[CV] fold=2 ..........................................................
[CV] fold=3 ..........................................................
[CV] fold=4 ..........................................................
[CV] fold=5 ..........................................................
[CV] fold=6 ..........................................................
[CV] fold=7 ..........................................................
[CV] fold=8 ..........................................................
[CV] fold=9 ..........................................................
predictions
{'test_score': array([1.35362847e+08, 1.20867167e+08, 1.48347243e+08, 2.49879706e+08,
        2.32217899e+08, 4.01511152e+08, 1.92061264e+08, 2.51755311e+08,
        1.50798724e+08, 1.92747682e+08]),
 'fit_time': array([0.28506732, 0.16709971, 0.17653751, 0.12498903, 0.1408143 ,
        0.16088152, 0.22708297, 0.33786058, 0.1593399 , 0.27807832]),
 'score_time': array([0.00801778, 0.        , 0.01562667, 0.        , 0.01132369,
        0.        , 0.01562595, 0.        , 0.01562929, 0.        ])}
np.sqrt(predictions["test_score"])
array([11634.55400113, 10993.96047191, 12179.78831408, 15807.58382521,
       15238.69740534, 20037.7431982 , 13858.61697326, 15866.79900091,
       12280.01317219, 13883.35991075])

从结果来看，使用更少的训练集进行训练后，模型输出的RMSE大幅上升了，并且也没有变得更稳定，这说明当前模型下更大的训练集会更有利于模型的训练(不是每个时间序列都是这样)。尝试调整滑窗的window_size，就会发现RMSE下降到了与滚动交叉验证时相似的水平:

model=pm.ARIMA(order=(2,1,1),seasonal_order=(1,0,1,12),max_iter=500)
cv=model_selection.SlidingWindowForecastCV(h=24,step=1,window_size=132)
predictions=model_selection.cross_validate(model,data,cv=cv
                                            ,scoring="mean_squared_error"
                                            ,verbose=2
                                            ,error_score="raise")
[CV] fold=0 ..........................................................
[CV] fold=1 ..........................................................
[CV] fold=2 ..........................................................
[CV] fold=3 ..........................................................
[CV] fold=4 ..........................................................
[CV] fold=5 ..........................................................
[CV] fold=6 ..........................................................
[CV] fold=7 ..........................................................
[CV] fold=8 ..........................................................
[CV] fold=9 ..........................................................
[CV] fold=10 .........................................................
[CV] fold=11 .........................................................
[CV] fold=12 .........................................................
[CV] fold=13 .........................................................
[CV] fold=14 .........................................................
[CV] fold=15 .........................................................
[CV] fold=16 .........................................................
[CV] fold=17 .........................................................
[CV] fold=18 .........................................................
[CV] fold=19 .........................................................
[CV] fold=20 .........................................................
predictions
{'test_score': array([35707121.78143389, 66176325.69903485, 40630659.97659013,
        78576782.28645307, 23666490.55159284, 20310751.60353827,
         2841898.1720445 ,  4484619.0619739 , 18925627.1367884 ,
         3231920.46993413, 55955063.23334328,  5769421.1274077 ,
        12204785.2577201 , 81763866.37114508, 86166090.62031393,
         4308494.01384212,  4472068.45984436, 80544390.23157245,
        95444224.35956413,  4356301.4101477 , 41312817.67528097]),
 'fit_time': array([0.98685646, 1.00776458, 0.98309445, 0.98523855, 0.99820113,
        0.88483882, 1.14556432, 0.94388413, 0.95140123, 1.01311779,
        1.01590633, 1.06021142, 1.05152464, 1.06878543, 1.08534598,
        1.07379961, 0.96942186, 0.92225981, 0.95834565, 1.33569884,
        0.91161823]),
 'score_time': array([0.01562262, 0.01562762, 0.        , 0.00460625, 0.        ,
        0.00678897, 0.00810504, 0.01536226, 0.01825047, 0.00629425,
        0.00742435, 0.01564217, 0.        , 0.        , 0.        ,
        0.        , 0.00800204, 0.01618385, 0.        , 0.01562595,
        0.        ])}
np.sqrt(predictions["test_score"])
array([5975.54363899, 8134.88326278, 6374.21838162, 8864.35458939,
       4864.82173893, 4506.74512298, 1685.79303951, 2117.69191857,
       4350.35942616, 1797.75428519, 7480.31170696, 2401.96193296,
       3493.53477981, 9042.33743958, 9282.56918209, 2075.69121351,
       2114.72656858, 8974.65265242, 9769.55599603, 2087.17546223,
       6427.50477832])

此时RMSE的均值大幅下降了，但是模型还是不稳定（波动较大），这说明当前时间序列各时间段上的差异较大,当前模型的拟合结果一般。虽然通过增加训练集的数据量可以让模型表现提升，但极其不稳定的结果展示当前模型的泛化能力是缺失的。和使用AIC时一样，我们只能选择表现更好的时序模型(只能择优)，而无法选择完美的时序模型。当我们将auto_arima选出的最佳参数放弃、而选择带有其他参数的模型，说不定得到的结果会更加不稳定。

        你是否注意到一个细节?时序交叉验证不会返回训练集上的分数，同时pmdarima的预测功能predict中也不接受对过去进行预测。通常来说我们判断过拟合的标准是训练集上的结果远远好于测试集，但时序交叉验证却不返回训练集分数，因此时间序列数据无法通过对比训练集和测试集结果来判断是否过拟合。但在时间序列的世界中，依然存在着”过拟合”这个概念，我们可以通过交叉验证的结果来判断不同参数下的时间序列模型哪个过拟合程度更轻。
        通常来说，验证集上的分数最佳的模型过拟合风险往往最小，因为当一个模型学习能够足够强、且既不过拟合又不欠拟合的时候，模型的训练集和验证集分数应该是高度接近的，所以验证集分数越好，验证集的分数就越可能更接近训练集上的分数。因此在多个模型对比的情况下，我们可以只通过观察测试集上的分数来选定最佳模型。这个最佳模型即是表现最佳的模型，也是过拟合风险最小的模型(不是绝对)。
 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1155085.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【C++代码】分割等和子集，目标和，一和零，零钱兑换，动态规划--代码随想录

【C++代码】分割等和子集，目标和，一和零，零钱兑换，动态规划--代码随想录

题目&#xff1a;分割等和子集 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集&#xff0c;使得两个子集的元素和相等。 初步想法排序后双指针&#xff0c;发现不行 class Solution { public:bool canPartition(vector<int>&…
阅读更多...
黑马 小兔鲜儿 uniapp 小程序开发- 商品详情模块- day05

黑马 小兔鲜儿 uniapp 小程序开发- 商品详情模块- day05

黑马 小兔鲜儿 uniapp 小程序开发- 分类模块- day04-CSDN博客 小兔鲜儿 - 商品详情(登录前)-day05 商品详情页分为两部分讲解&#xff1a; 登录前&#xff1a;展示商品信息&#xff0c;轮播图交互&#xff08;当前模块&#xff09;登录后&#xff1a;加入购物车&#xff0c;立…
阅读更多...
玩转硬件之Micro:bit的玩法(一)

玩转硬件之Micro:bit的玩法(一)

写在前面 这么长时间以来一直在玩软件, 好像软件还没有研究明白&#xff0c;因为工作的转变&#xff0c;又开始接触到硬件&#xff0c;既然开始触碰到硬件了&#xff0c;也想记录一下。有的时候想想要不要写这段前言&#xff0c;但是不写又觉得比较突兀&#xff0c;好端端的怎…
阅读更多...
python函数的定义与调用

python函数的定义与调用

python定义函数和函数的使用 函数 函数是对程序逻辑进行结构化或过程化的一种编程方法&#xff0c;将整块代码巧妙地隔离成易于管理的小块。把重复代码放到函数中而不是进行大量的拷贝&#xff0c;这样既能节省空间&#xff0c;也有助于保持一致性&#xff1b;通常函数都是用…
阅读更多...
【数据结构】数组和字符串（十三）：链式字符串的基本操作（串长统计、查找、复制、插入、删除、串拼接）

【数据结构】数组和字符串（十三）：链式字符串的基本操作（串长统计、查找、复制、插入、删除、串拼接）

文章目录 4.3 字符串4.3.1 字符串的定义与存储4.3.2 字符串的基本操作&#xff08;链式存储&#xff09;1. 结构体2. 初始化3. 判空4. 串尾添加5. 打印6. 串长统计7. 查找8. 复制9. 插入10. 删除11. 串拼接12. 销毁13. 主函数14. 代码整合 4.3 字符串 字符串(String)是由零个或…
阅读更多...
CodeGeeX：对标GitHub Copilot，国产免费可用的代码补全助手

CodeGeeX：对标GitHub Copilot，国产免费可用的代码补全助手

大家好&#xff0c;我是豆小匠。 本期介绍的插件CodeGeeX&#xff0c;是一款免费的智能编程助手。 主要功能是代码生成和补全&#xff0c;但不止于此&#xff01; CodeGeeX介绍 CodeGeeX是清华大学和智谱AI联合打造的多语言代码生成模型。 第一代是完全在华为昇腾芯片平台训练…
阅读更多...
华为OD机考算法题：生日礼物

华为OD机考算法题：生日礼物

题目部分 题目生日礼物难度易题目说明小牛的孩子生日快要到了&#xff0c;他打算给孩子买蛋糕和小礼物&#xff0c;蛋糕和小礼物各买一个&#xff0c;他的预算不超过x元。蛋糕 cake 和小礼物 gift 都有多种价位的可供选择。输入描述第一行表示cake的单价&#xff0c;以逗号分隔…
阅读更多...
③ 软件工程CMM、CMMI模型【软考中级-软件设计师 考点】

③ 软件工程CMM、CMMI模型【软考中级-软件设计师 考点】

个人简介&#xff1a;Java领域新星创作者&#xff1b;阿里云技术博主、星级博主、专家博主&#xff1b;正在Java学习的路上摸爬滚打&#xff0c;记录学习的过程~ 个人主页&#xff1a;.29.的博客 学习社区&#xff1a;进去逛一逛~ ③ 软件工程CMM、CMMI模型【软考中级-软件设计…
阅读更多...
SpringCloud Alibaba Demo(Nacos,OpenFeign,Gatway,Sentinel)

SpringCloud Alibaba Demo(Nacos,OpenFeign,Gatway,Sentinel)

开源地址&#xff1a; ma/springcloud-alibaba-demo 简介 参考&#xff1a;https://www.cnblogs.com/zys2019/p/12682628.html SpringBoot、SpringCloud 、SpringCloud Alibaba 以及各种组件存在版本对应关系。可参考下面 版本对应 项目前期准备 启动nacos. ./startup.c…
阅读更多...
营收净利双降、股价下跌四成，敷尔佳带伤闯关“双11”

营收净利双降、股价下跌四成，敷尔佳带伤闯关“双11”

今年双11预售已经开启&#xff0c;敷尔佳在天猫、抖音等电商平台火热营销&#xff1b;营销热业绩冷&#xff0c;敷尔佳的三季报不及预期。 10月23日&#xff0c;哈尔滨敷尔佳科技发展有限公司(下称“敷尔佳”&#xff0c;301371SZ)公布2023年三季报&#xff0c;其三季度营收净…
阅读更多...
【C++ 系列文章 -- 程序员考试 下午场 C++ 专题 201805 】

【C++ 系列文章 -- 程序员考试 下午场 C++ 专题 201805 】

文章目录 1.1 C 题目六1.1.1 填空&#xff08;1&#xff09;详解1.1.1.1 C 纯虚函数介绍 1.1.2 填空&#xff08;2&#xff09;详解1.1.2.1 父类声明了带参构造函数1.1.2.2 子类中构造函数的构造原则 1.1.3 填空&#xff08;3&#xff09;详解1.1.4 填空&#xff08;4&#xff…
阅读更多...
Python小试牛刀：GUI（图形界面）实现计算器界面

Python小试牛刀：GUI（图形界面）实现计算器界面

Python GUI 是指 Python 图形用户界面库&#xff0c;它们可以帮助开发者创建在计算机上运行的图形用户界面&#xff08;GUI&#xff09;。下面是一些常用的 Python GUI 库&#xff1a; Tkinter&#xff1a; Tkinter 是 Python 的标准 GUI 库&#xff0c;它是一个开源的、跨平台…
阅读更多...
LeetCode刷题之 存在重复元素（题目分析➕源代码）

LeetCode刷题之 存在重复元素（题目分析➕源代码）

题目链接&#x1f517;力扣&#xff08;LeetCode&#xff09;官网 - 全球极客挚爱的技术成长平台 1. 题目分析 本题是要找到数组中的重复元素&#xff0c;所以我们分析出一下几点&#xff1a; 1. bool是一种数据类型&#xff0c;true是非0值&#xff0c;false是0.。 2. 数组…
阅读更多...
绘制教材P68页产品的层次方框图。

绘制教材P68页产品的层次方框图。

层次方框图&#xff1a; 用树形结构的一系列多层次的矩形框绘制数据的层次结构&#xff0c;树形结构的顶层是一个单独的矩形框&#xff0c;它代表完整的数据结构&#xff0c;下面的各层矩形框代表这个数据的子集&#xff0c;最底层的各个框代表组成这个数据的实际数据元素&…
阅读更多...
verilog语言学习

verilog语言学习

1. 时延 2. 一位全加器设计&#xff1a;三种建模方式 实际的设计中往往是这三种设计模式的混合 3. 4. 5. 6. 7. 建立模型时信号的连接&#xff08;重点&#xff09; 8. initial语句 9. always语句 在always中不能同时判断同一个信号的上升沿&#xff08;posedge&#xff0…
阅读更多...
网工内推 | IDC网工、运维，上市公司，主流厂商认证优先，六险一金

网工内推 | IDC网工、运维，上市公司，主流厂商认证优先，六险一金

01 软通动力 招聘岗位&#xff1a;ICD机房运维工程师 职责描述&#xff1a; 1.维护及管理数据中心内各类服务器及网络设备。 2.处理数据中心各类服务器和网络相关故障和告警。 3.负责数据中心内项目交付管理&#xff0c;包括LLD评审、硬装工艺验收、ASP施工管理等。 4.负责数据…
阅读更多...
什么是互动广告

什么是互动广告

随着数字技术的迅速发展和消费者行为的转变&#xff0c;互动广告已成为现代广告行业的重要组成部分。互动广告以其独特的优势和形式&#xff0c;不断刷新人们对广告的认知&#xff0c;为广告行业带来新的机遇和挑战&#xff0c;那么就来一起了解互动广告吧。 一、互动广告的定义…
阅读更多...
笔记49：53语言模型--课程笔记

笔记49：53语言模型--课程笔记

本地笔记地址&#xff1a;D:\work_file\DeepLearning_Learning\03_个人笔记\3.循环神经网络\语言模型 PS&#xff1a;沐神别怪我&#xff0c;实在是截屏避不开啊&#xff0c;我就留个备忘&#xff0c;在我博客里先委屈一下哈&#xff0c;对不住了 a a a a a a a a a a…
阅读更多...
二十一、Arcpy批量镶嵌——结合Landsat数据提取城市建成区

二十一、Arcpy批量镶嵌——结合Landsat数据提取城市建成区

一、前言 前文介绍Pycharm软件安装和激活，以及运行环境的设置，本文就详细介绍一下几何Landsat数据有哪些步骤可以通过Arcpy代码来实现批量操作，其实主要集中在Landsat数据预处理过程中，包括数据镶嵌、裁剪、去背景、重采样以及波段组合计算、NDVI、NDBI计算，在一定程度上…
阅读更多...
JetBrains TeamCity远程命令执行漏洞

JetBrains TeamCity远程命令执行漏洞

一、免责声明&#xff1a; 本次文章仅限个人学习使用&#xff0c;如有非法用途均与作者无关&#xff0c;且行且珍惜&#xff1b;由于传播、利用本公众号所提供的信息而造成的任何直接或者间接的后果及损失&#xff0c;均由使用者本人负责&#xff0c;公众号望雪阁及作者不为此承…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023