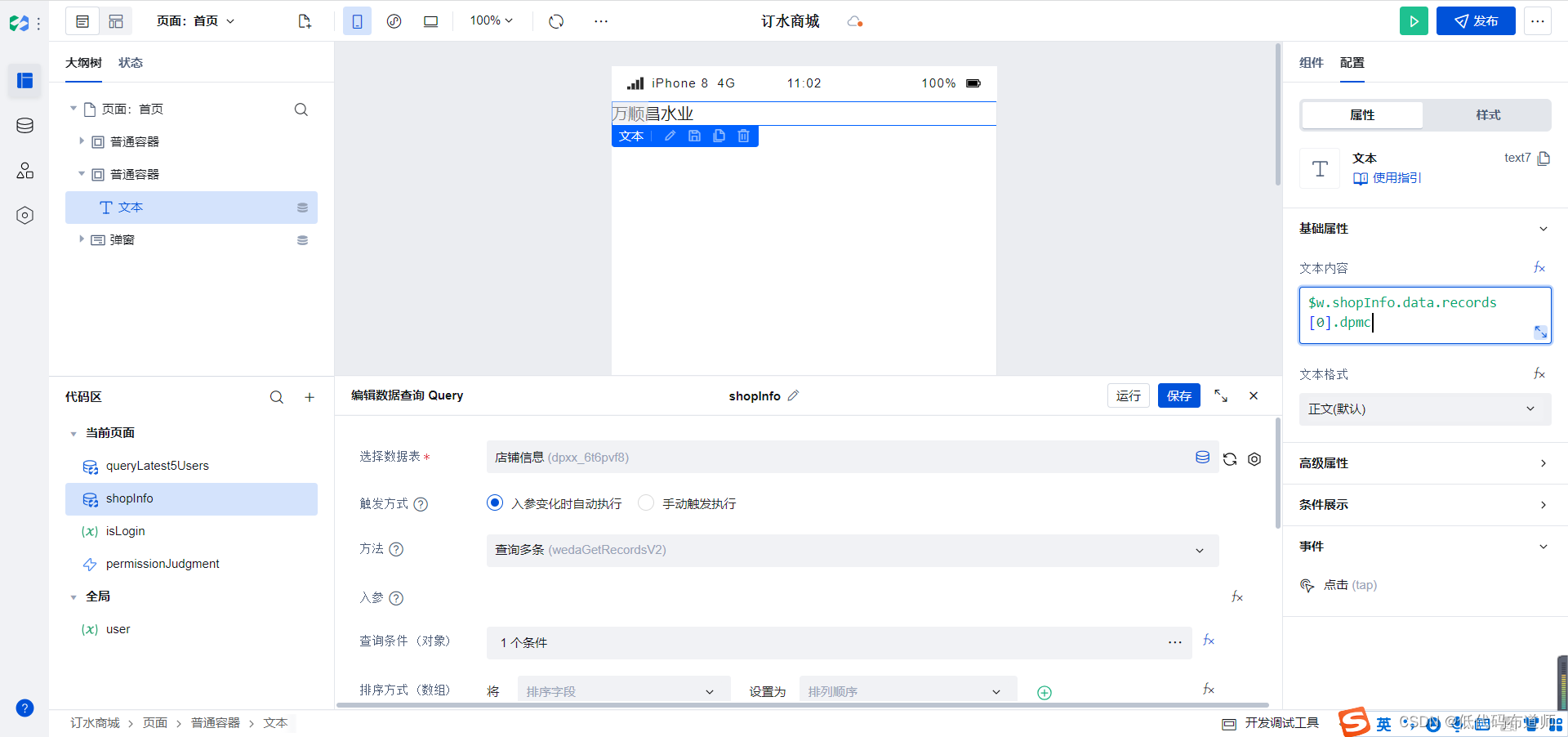
Data Stream Review
- Overall
- Uniform Sampling
- Bloom Filter
- Misra-Gries Algorithm
- CountMin Sketch Algorithm
- Count Sketch Algorithm
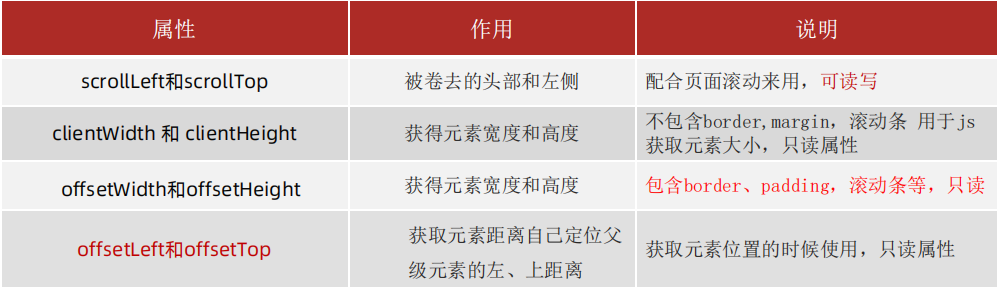
Overall
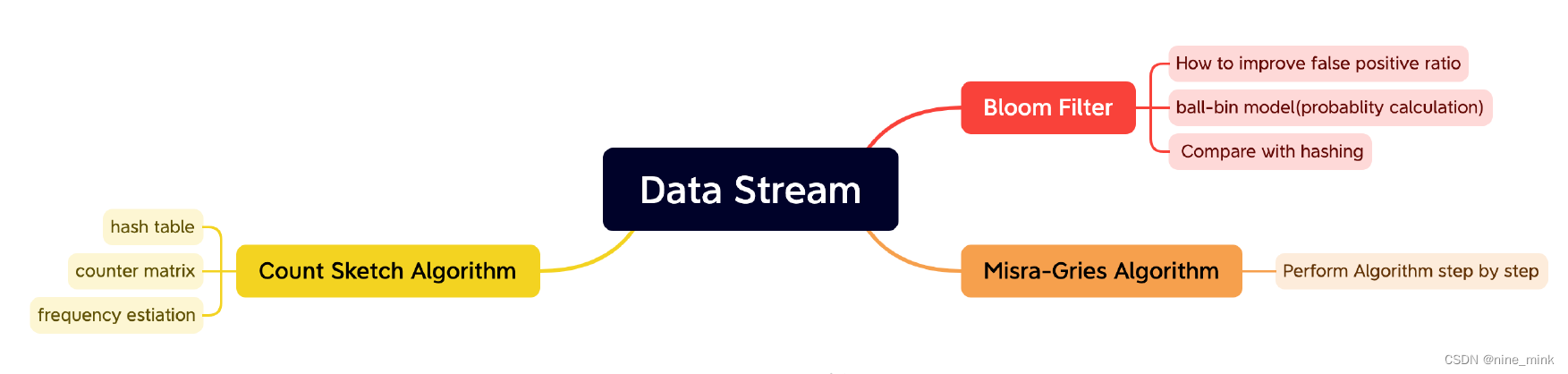
Uniform Sampling
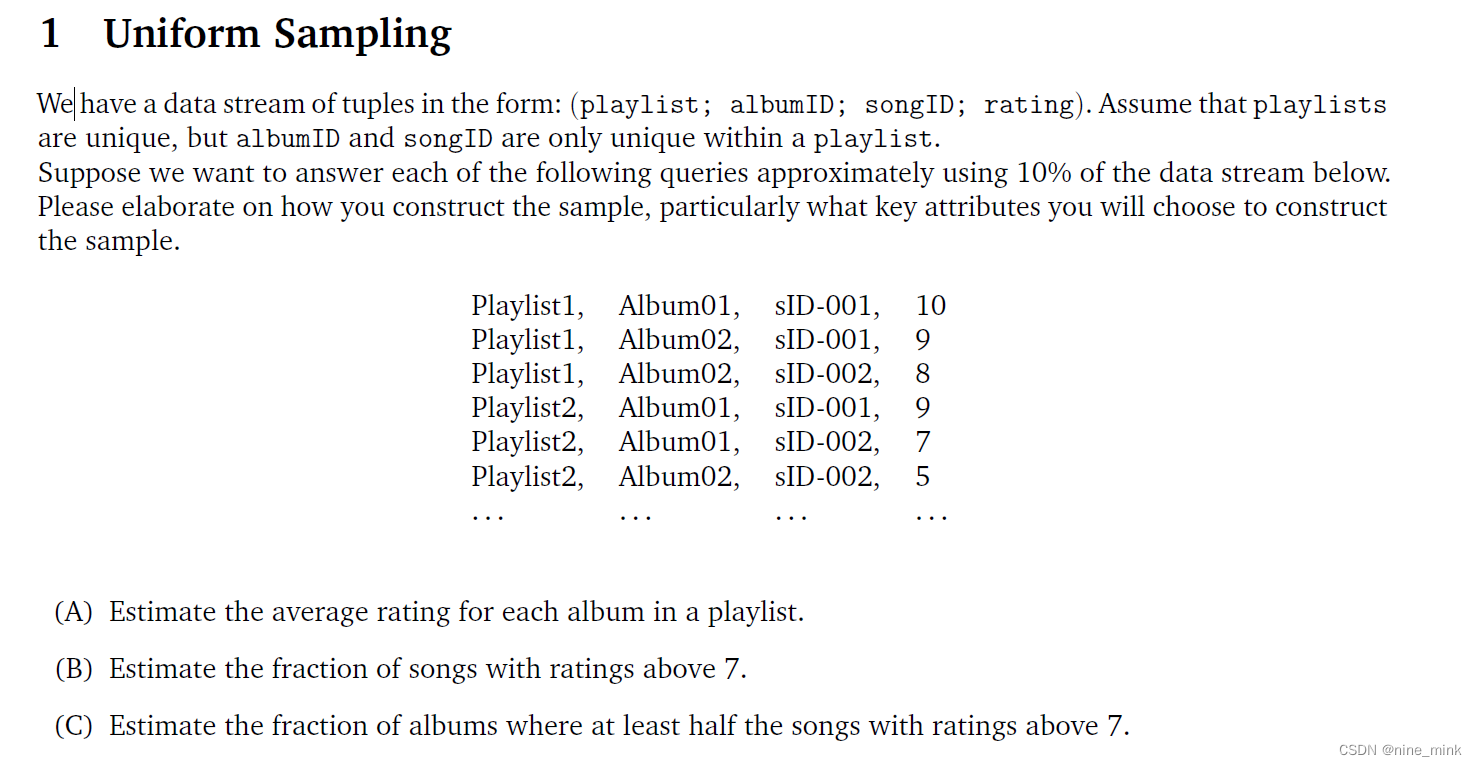
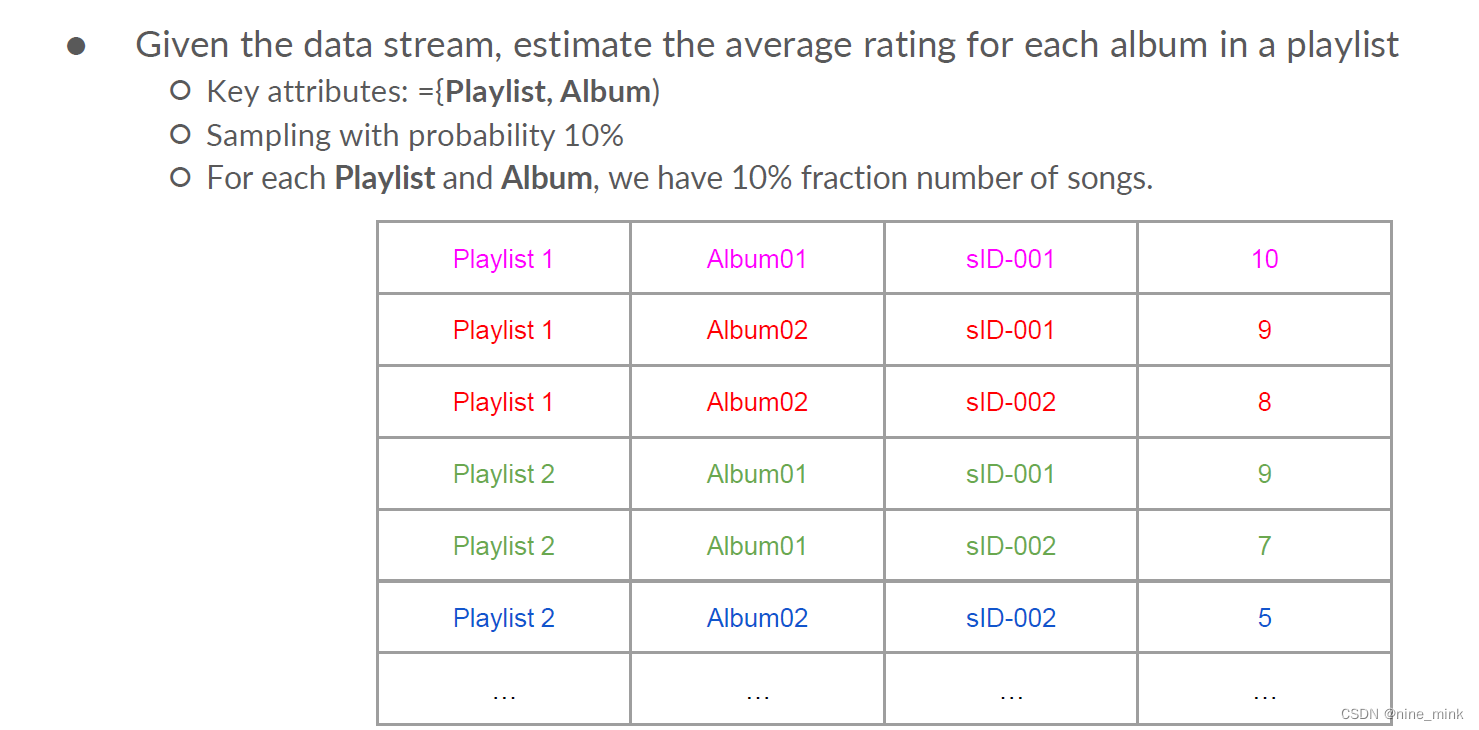
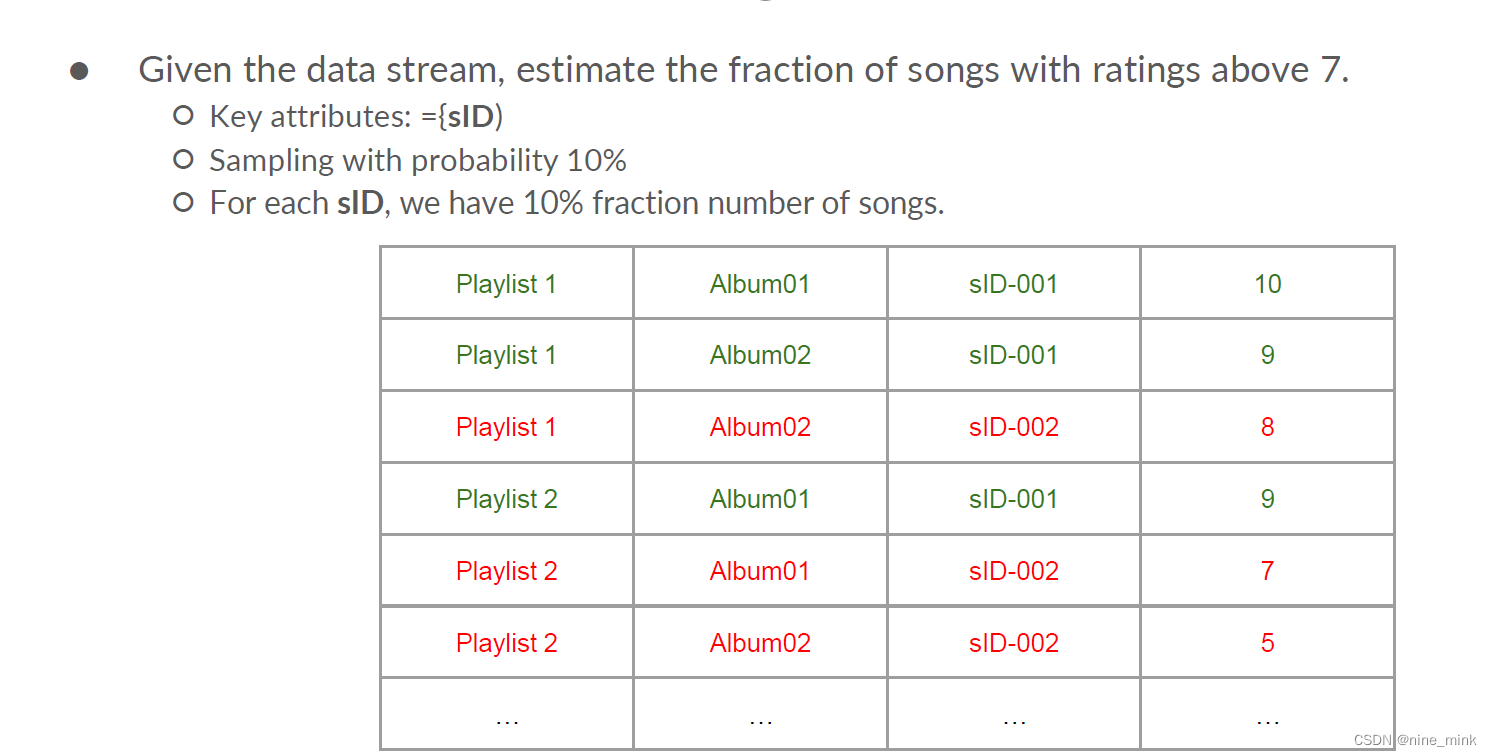

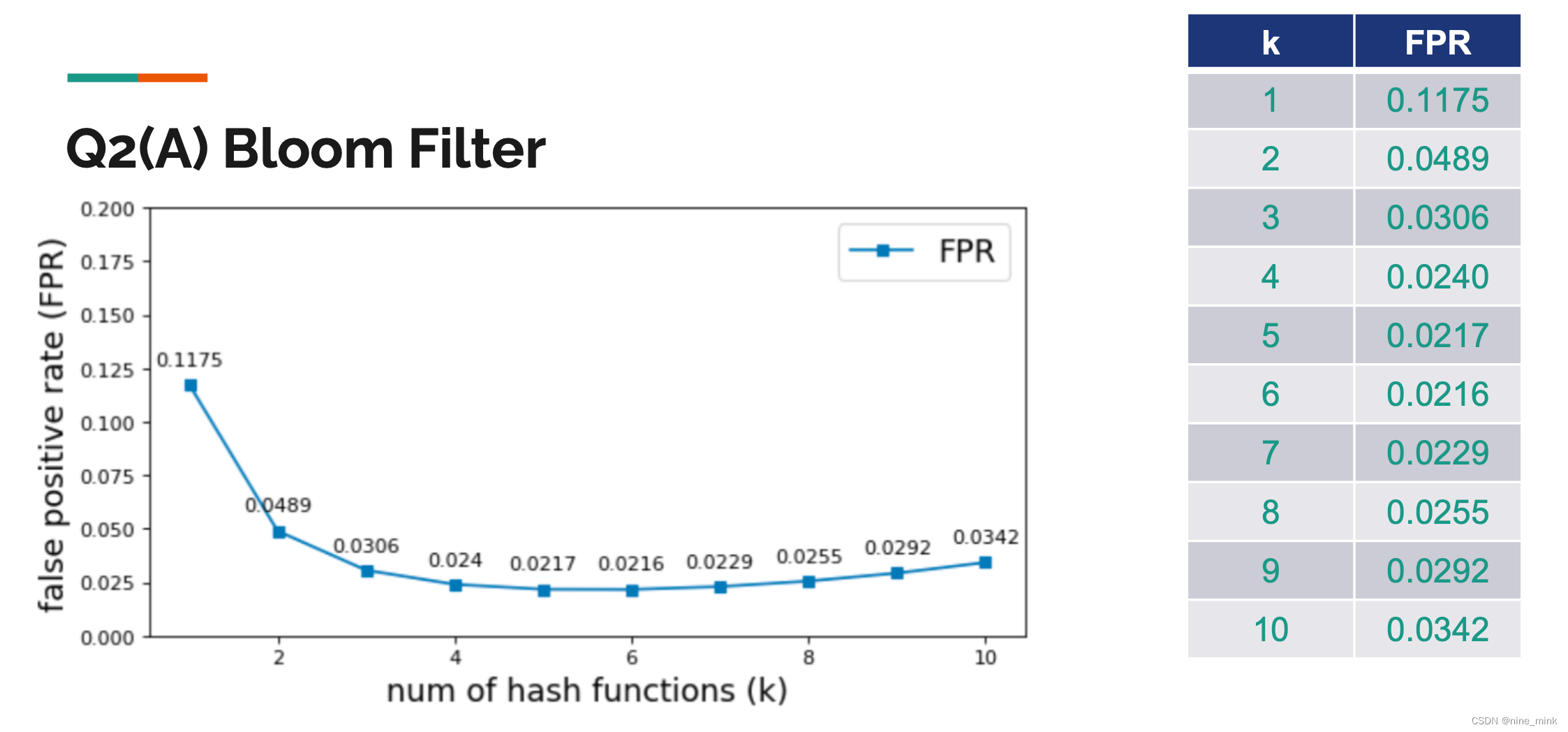
Bloom Filter

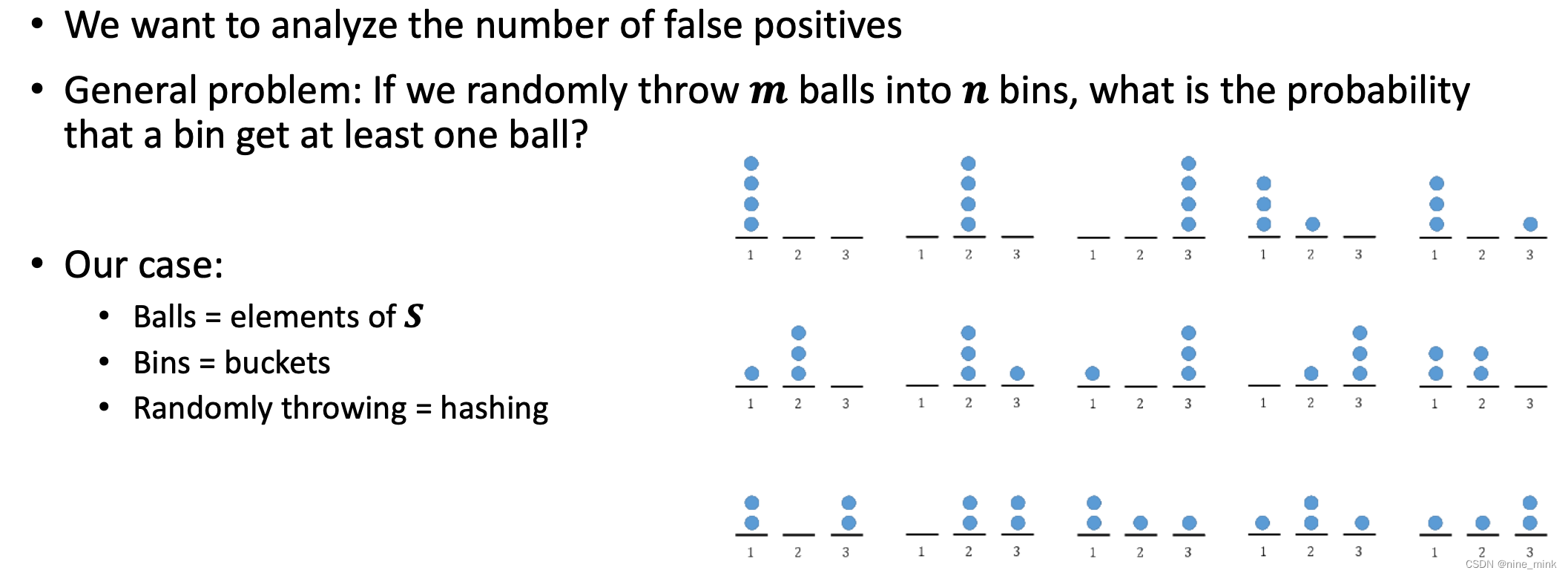

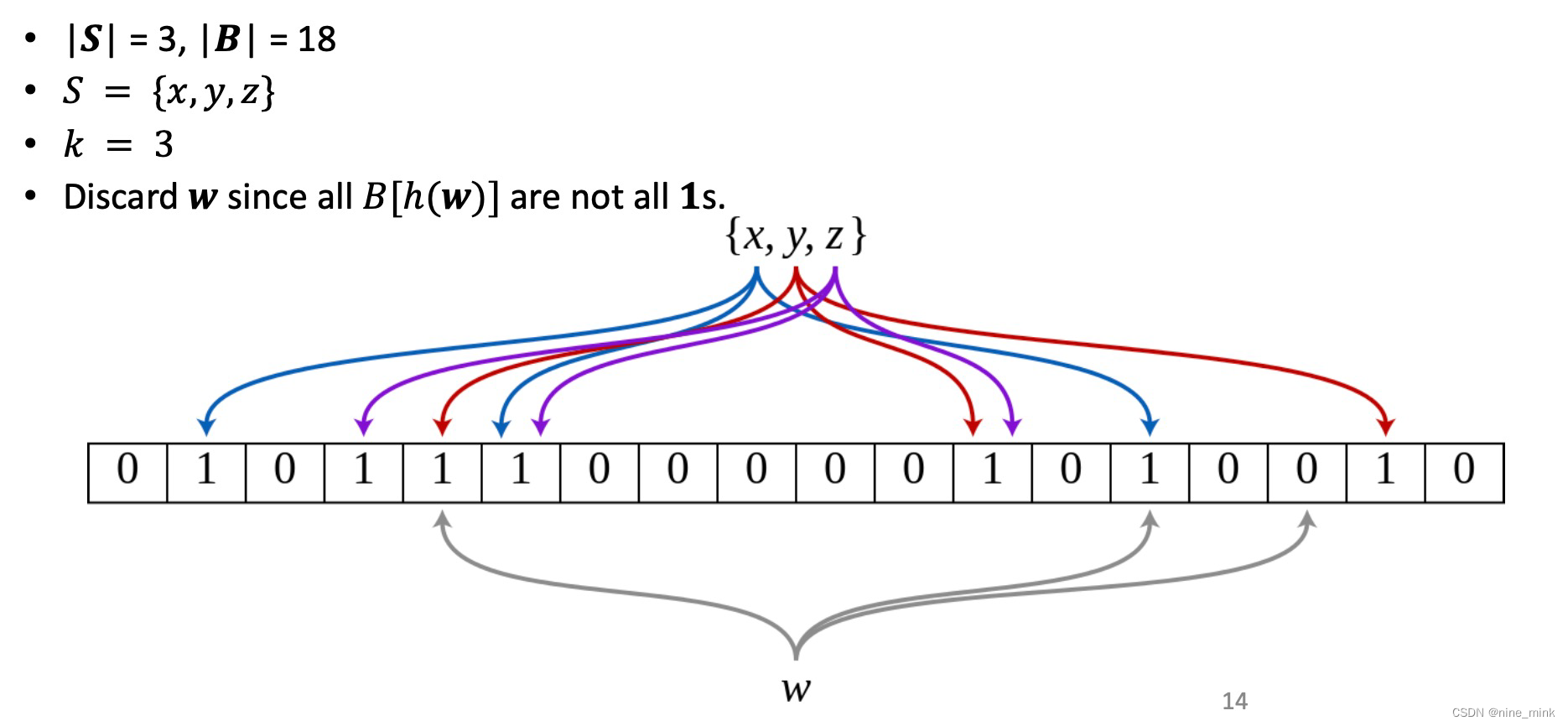




一个箱子没有球的概率可以表示为 (1 - 1/n)^m 的原因是基于以下逻辑:
-
对于第一个球,它可以被放入 n 个箱子中的任何一个,因此每个箱子都有 1/n 的概率收到第一个球。
-
对于第二个球,同样地,每个箱子都有 1/n 的概率收到第二个球,因为球被放入箱子的概率是相同的,而且与之前球放在哪个箱子无关。
-
对于第三个球,同样地,每个箱子都有 1/n 的概率收到第三个球,以此类推。
因此,每个球被放入一个箱子的概率都是 1/n,而且这些概率是相互独立的,因为一个球的放置不受另一个球的放置影响。
要计算一个箱子没有球的概率,我们可以考虑它不收到任何球的概率。这就相当于每个球都不被放入这个箱子的概率,即 (1 - 1/n)。因为每个球的放置是相互独立的,所以多个球都不被放入这个箱子的概率就是这些独立事件的乘积。
所以,一个箱子没有球的概率是 (1 - 1/n)^m,其中 m 是球的数量,n 是箱子的数量。这个公式表示了每个箱子都至少有一个球的补集的概率。

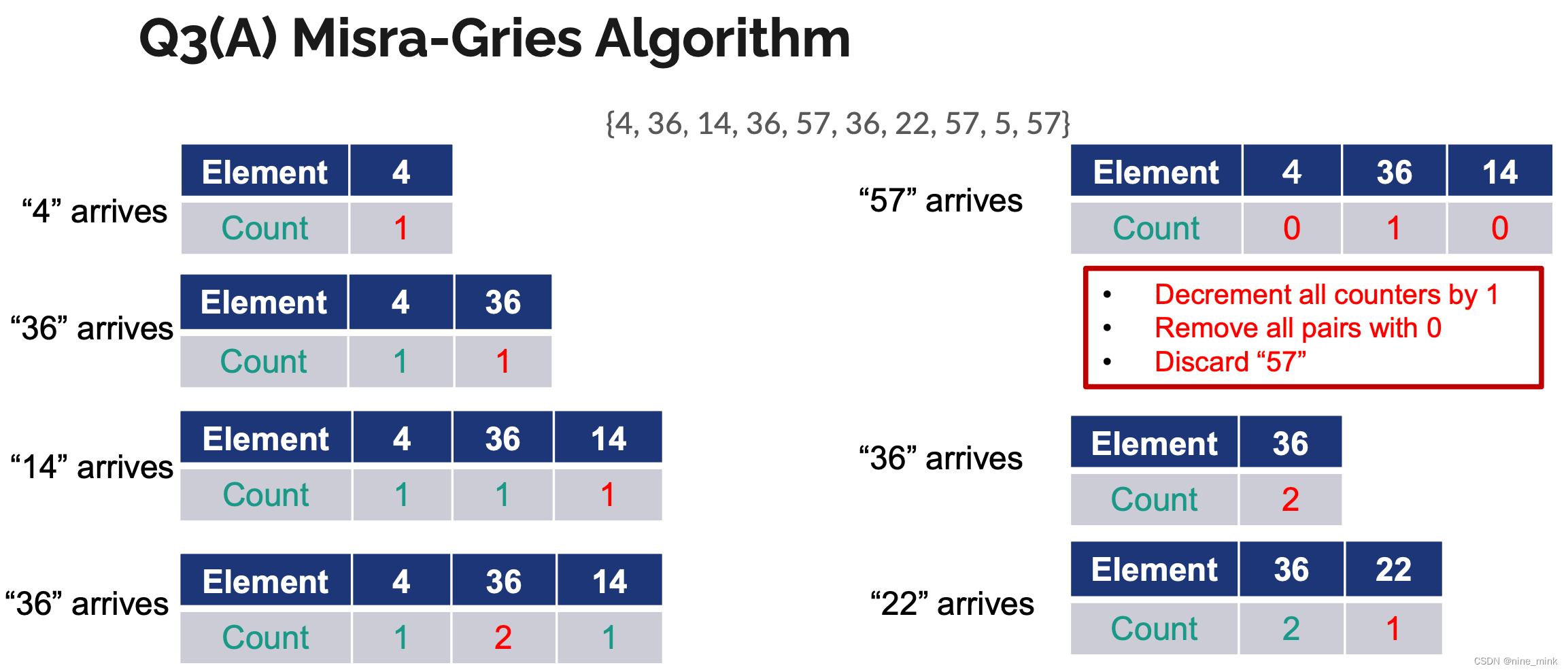
Misra-Gries Algorithm






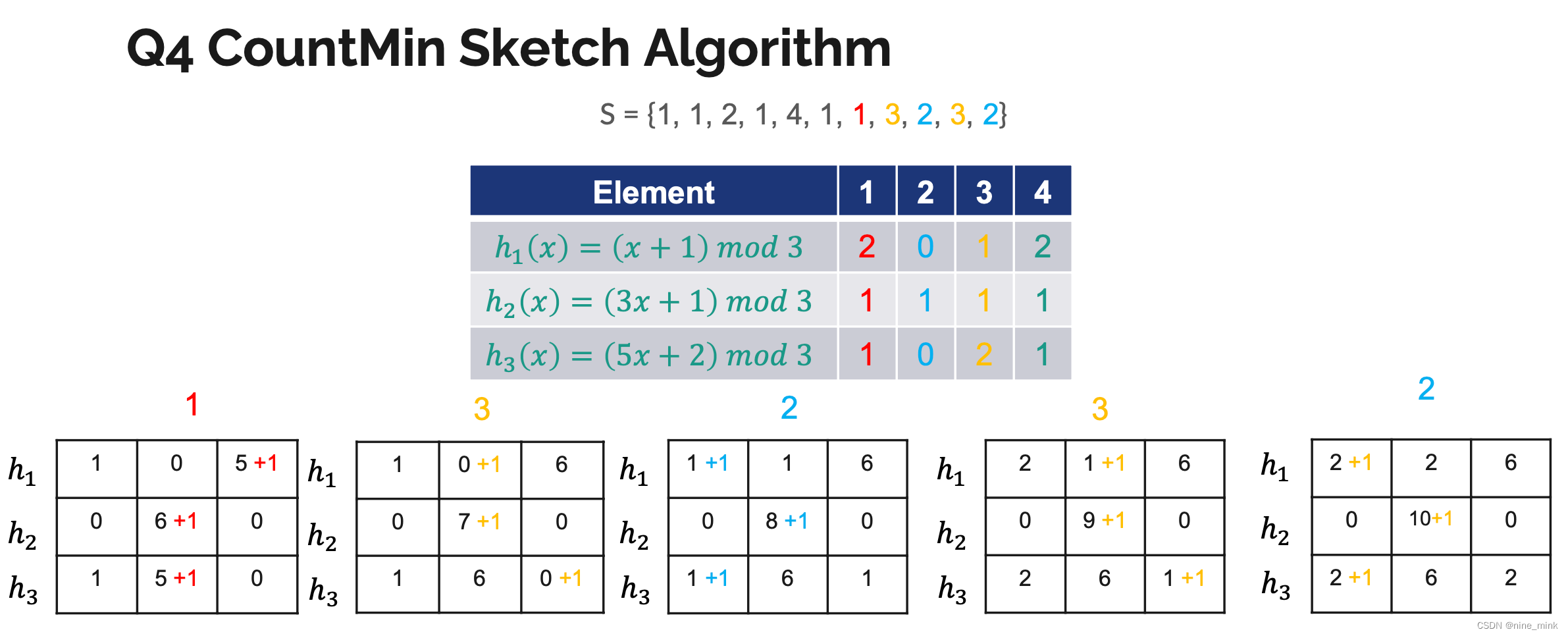
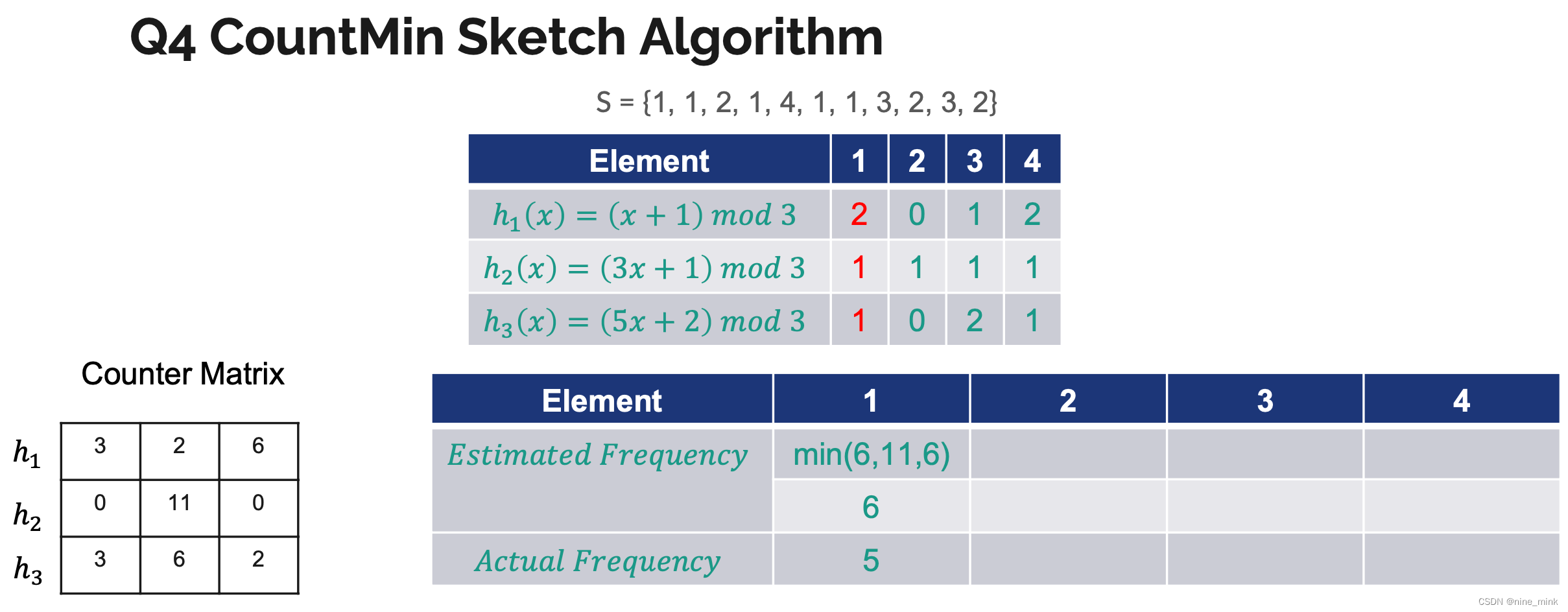
CountMin Sketch Algorithm
Count-Min Sketch 是数据库中用到的一种Sketch,所谓sketch 就是用很少的一点数据来描述全体数据的特性,牺牲了准确性但是代价变得很低。
CM-Sketch 的内部数据结构是一个二维数组count,宽度w,深度d,此外还需要d个两两独立的哈希函数h1…hd 更新的时候,用这些哈希函数算出d个不同的哈希值,然后把对应的行的值加上
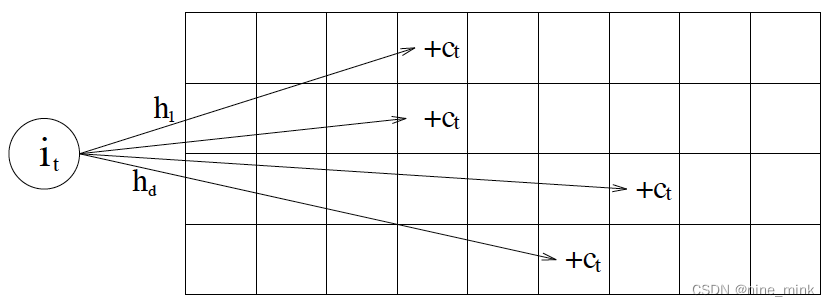



W: hash之后的值域,即0,1,2
D:hash函数的数量

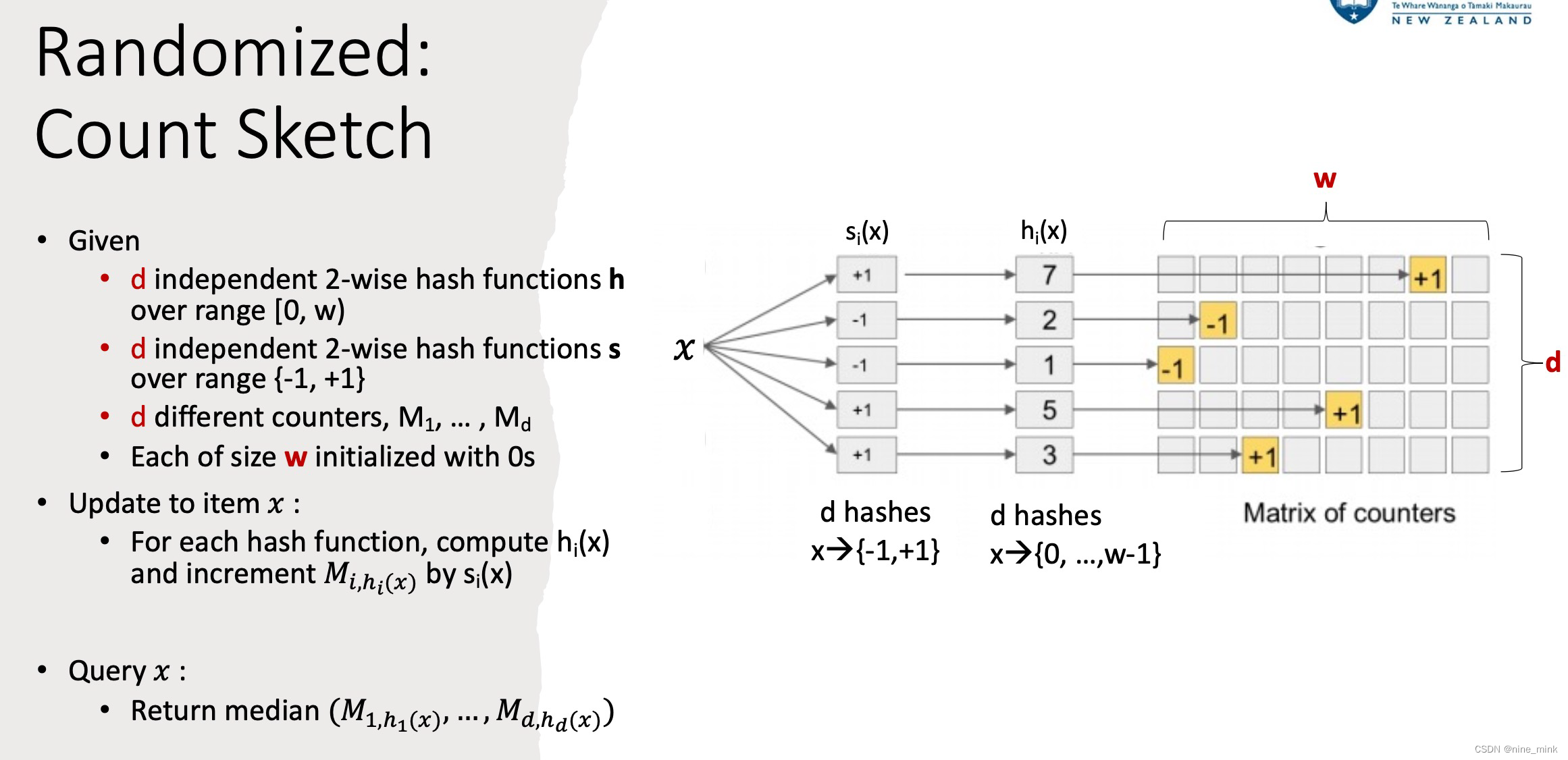
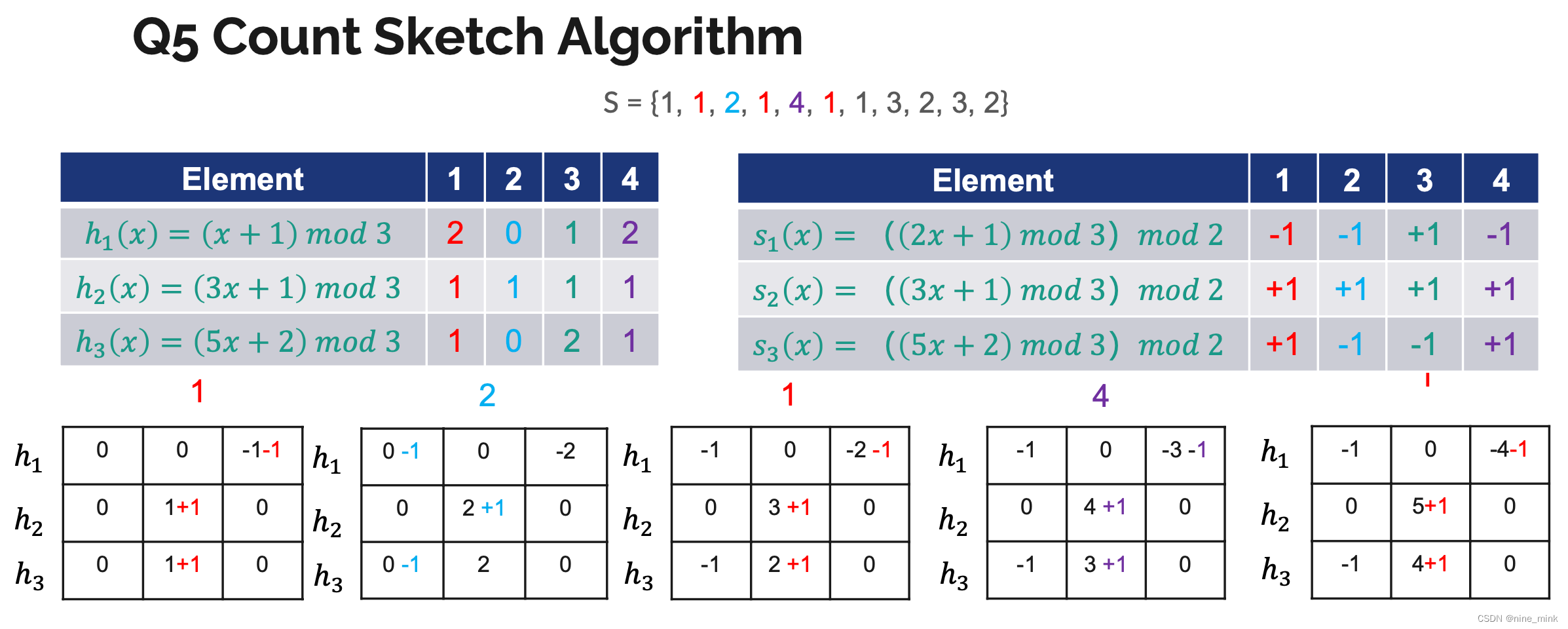
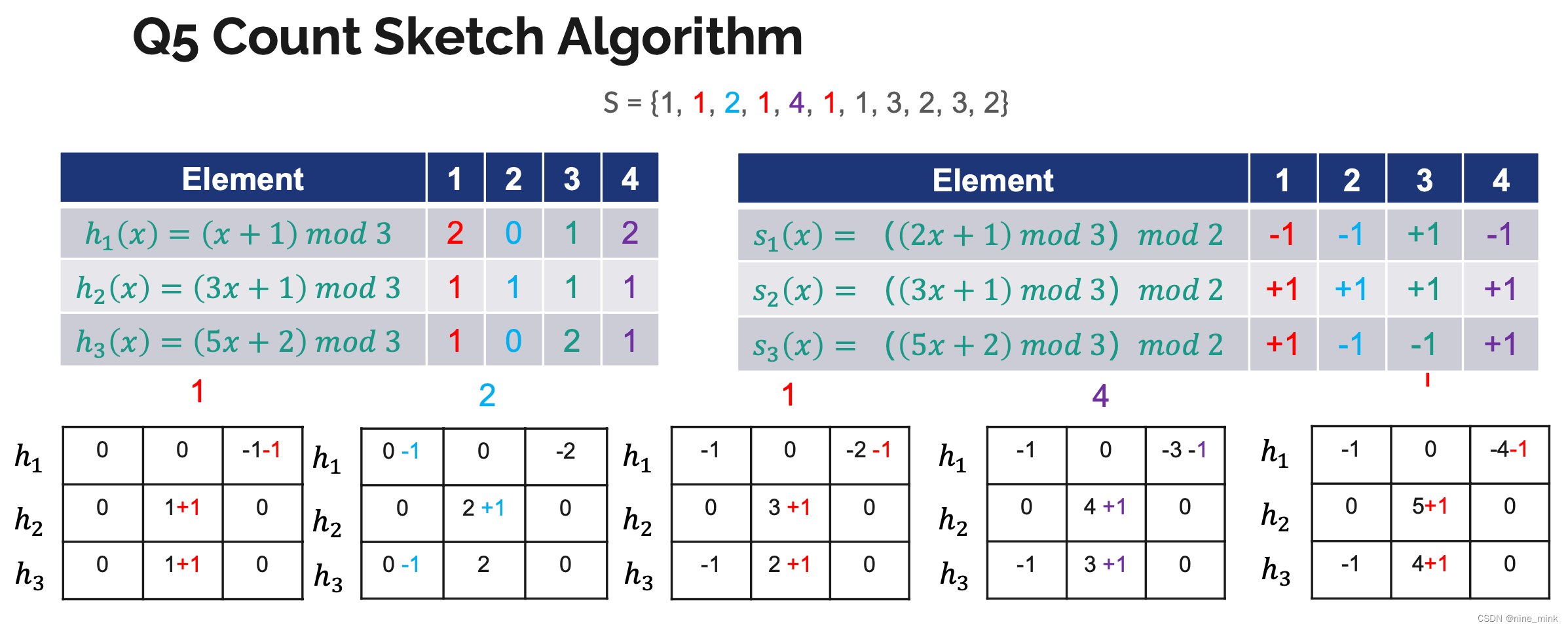
Count Sketch Algorithm
运行sketch方法k次,每次对应单独的哈希函数h(索引到数组某个位置)和g(哈希函数g的目的是无偏估计),然后取结果的平均值。





![[双指针] (三) LeetCode LCR 179. 查找总价格为目标值的两个商品 和 15. 三数之和](https://img-blog.csdnimg.cn/img_convert/a68be9eda0c5cd735110277576ef3769.png)