摘要

ROS中通过tf.TransformListener.lookupTransform方法获取从A坐标系到B坐标系的旋转四元数rot，通过quaternion_multiply函数实现$p^{\prime }=qp{q}^{-1}$中的矩阵乘法，从而可以方便获取在新坐标系下的四元数坐标表示$p^{\prime }$. 基于此，本博客提供将一个基于A坐标系下的三维向量变换到基于B坐标系下的标准代码模板和应用实例，便于后续查阅。

关键词

ROS， TF， 坐标系变换，四元数，向量表示

前言

在构建海洋机器人动力学模型的时候，其中的外力项通常要包含进风和海流的作用力，这些力在全局大地坐标系（静态坐标系）下的向量表示通常是放方向和大小都较为固定的常量，但是如果要将这些作用引入动力学模型，一般都是基于船体坐标系下的，而随着船体的位置和朝向的变化，风海流在船体坐标系下的向量表示，连同其三轴分量，一定时刻变化着。在得到风海流在大地坐标系下的向量表示后，如何快速求得其在船体坐标系下的分量？

在机器人执行目标跟踪任务的时候，由于机器人的路径规划算法中，目标的坐标表示一般是要基于以机器人中心为原点的坐标系下的，而目标检测的视觉算法得到的距离与偏角却是目标和机载摄像头之间的相对位置关系；如果还要知道目标在全局地图中的坐标，还需要进一步求得在大地坐标系下的位置表示。

这些问题的背后是同一个问题：基于A坐标系下的三维向量在另一个坐标系下的坐标是什么，如何快速求得？ 本博客提供了在ROS中快速实现实现将一个基于A坐标系下的三维向量变换到基于B坐标系下的标准代码模板和应用实例，便于后续查阅。

方法

基本思路

抽象为数学问题后可以表述为：假设一个三维实数空间向量$v$在坐标系A中表示为$v=[x,y,z]\in {\mathbb{R}}^3$，坐标系A到坐标系B的旋转可以用四元数向量为$q$，求空间向量$v$在坐标系B中的坐标表示。

求法是：首先将向量$v$用四元数$p$表达，用四元数表达的实数向量一定是一个虚四元数，即$p=[0,x,y,z]=[0,v]$，然后，向量$v$在B系中的四元数表示（设此四元数为$p^{\prime }$）即为$$p^{\prime }=qp{q}^{-1}$$ $p^{\prime }$也是一个虚四元数。

出处见下图：

(出处来源链接：https://www.cnblogs.com/gaoxiang12/p/5120175.html)

因此，在ROS中为了实现将一个基于A坐标系下的三维向量变换到基于B坐标系下，需要知道：

1. 向量在A系下的坐标；
2. 向量在A系下的坐标的四元数表示；
3. A系到B系变换的旋转四元数

最后，在ROS中实现矩阵乘法

$$p^{\prime }=qp{q}^{-1}$$

并取$p^{\prime }$四元数中的虚部部分即得到变换到基于B坐标系下后的坐标表示。

基本模板

# Neccessary library
import rospy
import tf
import tf2_ros

x,y,z = 1,2,3
vector = [x,y,z]
v_base_link= [vector[0], vector[1],vector[2], 0] 
listener = tf.TransformListener()
try:
	(trans,rot) = listener.lookupTransform('parent_frame', 'child_frame', rospy.Time(0))
    v_map = tf.transformations.quaternion_multiply(tf.transformations.quaternion_multiply(rot, v_base_link), tf.transformations.quaternion_conjugate(rot))
    v_new = v_map[0:3]
except Exception as e:
	print(f"Exception:{e}")
# ...

部分代码解释

# 假设向量v在A系中的坐标和对应的四元数表示
x,y,z = 1,2,3
vector = [x,y,z]
v_base_link= [vector[0], vector[1],vector[2], 0] 

# 实例化tf库中TransformListener类，利用该类的lookupTransform方法获取从A坐标系到B坐标系的旋转四元数rot
# 注意在本问题中，坐标系平移变换向量trans是不需要用到的
listener = tf.TransformListener()
try:
	(trans,rot) = listener.lookupTransform('parent_frame', 'child_frame', rospy.Time(0))

# 利用quaternion_multiply函数实现p' = qpq^{-1}中的矩阵乘法
v_map = tf.transformations.quaternion_multiply(tf.transformations.quaternion_multiply(rot, v_base_link), tf.transformations.quaternion_conjugate(rot))

细节问题

Q：四元数是一个向量，为什么会有逆？

四元数取逆其实是取共轭。

出处见下图：

(出处来源链接：https://zhuanlan.zhihu.com/p/52565002)

而tf.transformations.quaternion_conjugate(quaternion)的作用就是返回四元数的共轭。

出处见下图：
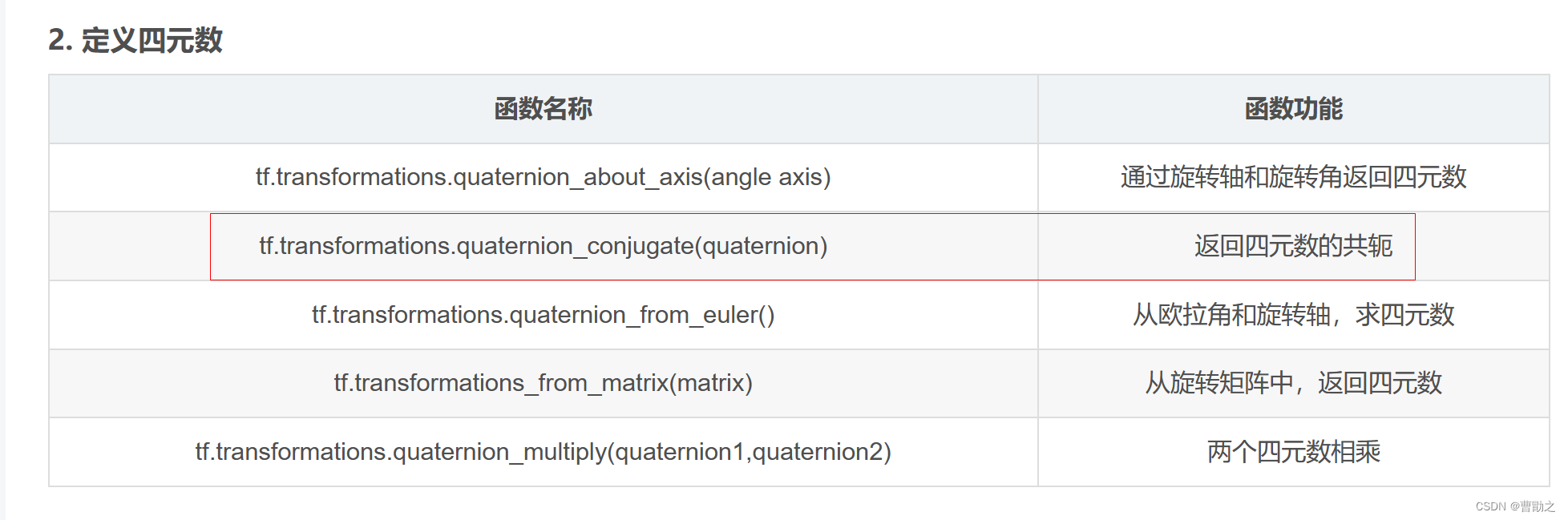(出处来源链接：https://blog.csdn.net/weixin_44682965/article/details/107818474)

Q：listener.lookupTransform的前两个参数中哪个是父系（源坐标系）哪个是子系（目标坐标系）？

第一个参数是源坐标系，第二个参数是目标坐标系。

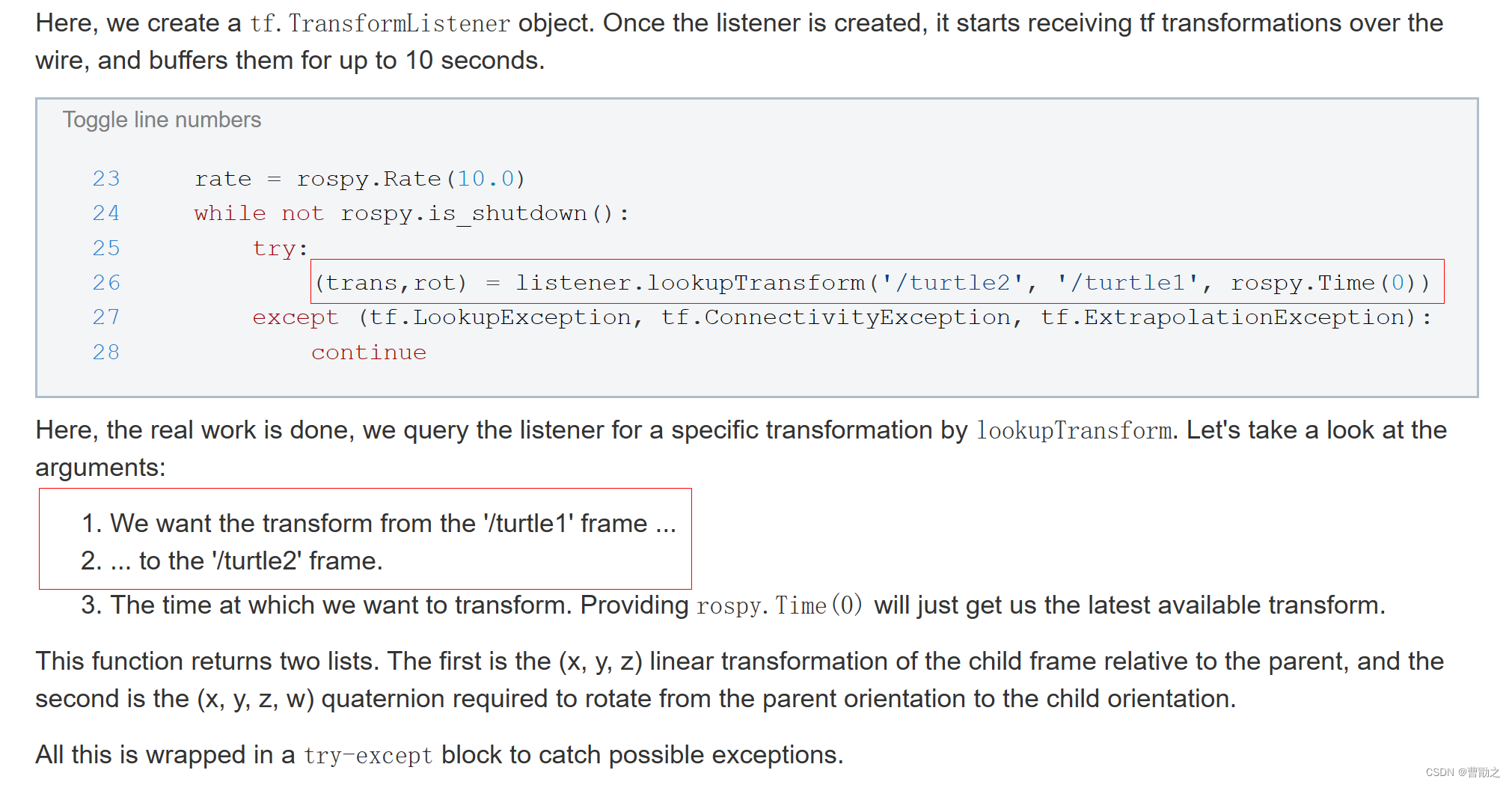
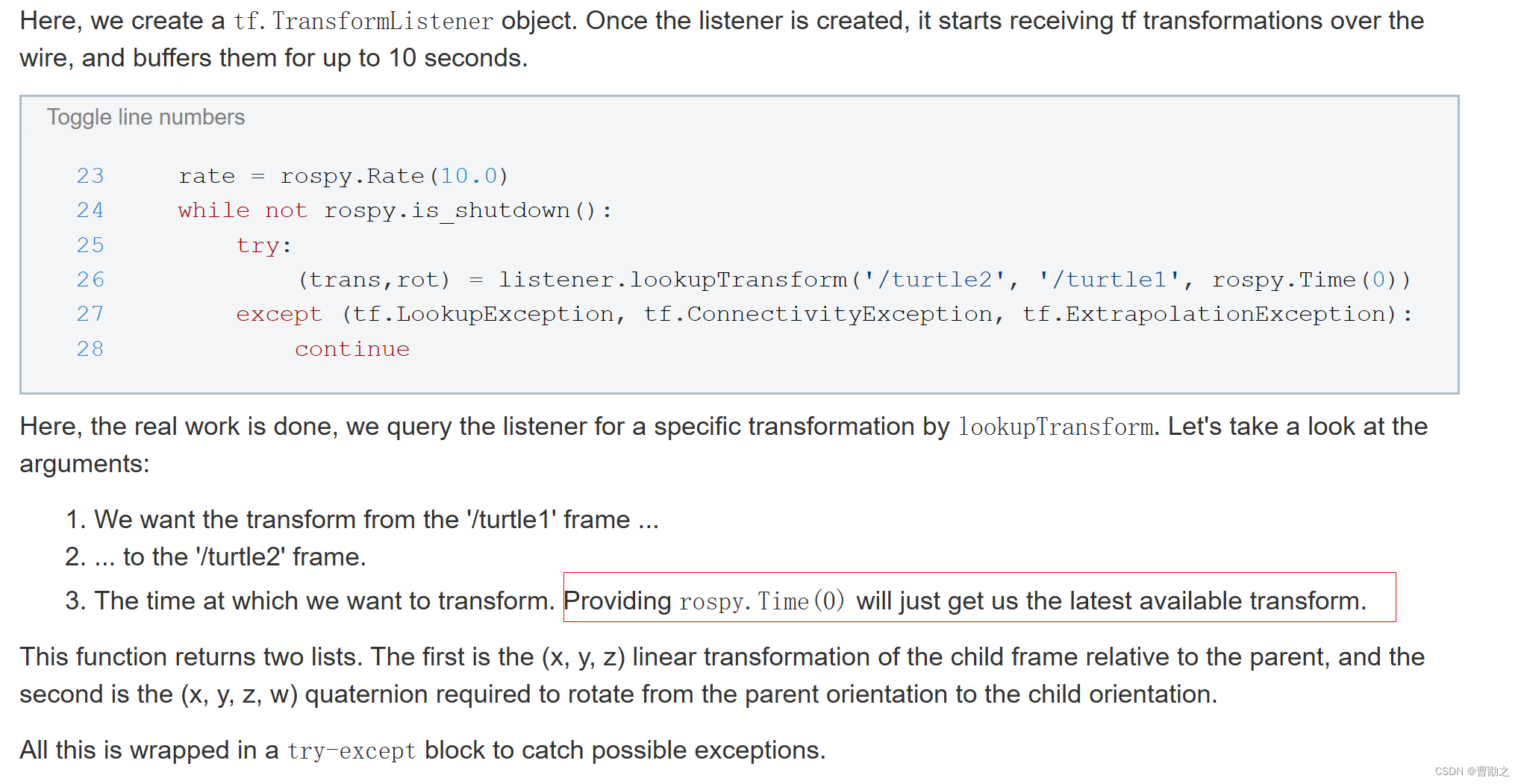
Q：rospy.Time(0)的作用？

获取距离调用listener.lookupTransform函数时间最近的rot变量。

出处见下图：

(出处来源链接：http://wiki.ros.org/tf/Tutorials/Writing%20a%20tf%20listener%20%28Python%29)

这也意味着，在程序执行一开始的时候，可能是没有可用的rot供获取的，这是需要使用try-except语句的原因。

Q：四元数在ROS中的排布？

• 数学上，一个四元数的表达若设置为[w,x,y,z]，则其中的w为实部，x,y,z为虚部。

出处见下图：

(出处来源链接：https://www.cnblogs.com/gaoxiang12/p/5120175.html)

• 在ROS中，这样的四元数是按如下顺序排布的：[x,y,z,w]，即将实部放在了最后。

出处见下图：

（来源链接：http://wiki.ros.org/tf2/Tutorials/Quaternions）。

应用

目标

承接在ROS中如何实现两个固定坐标系之间的变换？中应用部分的问题。在该问题中，新静态坐标系为NED（东北地坐标系），设向量$v$在world坐标系中的坐标表示是$v=[1,2,3]$，求该向量在NED坐标系中的坐标表示。

操作过程

1. 打开ROS中如何实现两个固定坐标系之间的变换？中应用部分的脚本
2. 修改代码。脚本代码如下（代码已经过测试）：

#!/usr/bin/env python3
# coding: utf-8

# Neccessary library
import rospy
import tf
import tf2_ros
import geometry_msgs.msg
import numpy as np

rospy.init_node("static_transformation")

static_transformStamped = geometry_msgs.msg.TransformStamped()

broadcaster = tf2_ros.StaticTransformBroadcaster()
static_transformStamped.header.stamp = rospy.Time.now()
static_transformStamped.header.frame_id = "world"
static_transformStamped.child_frame_id = "NED"
# ...此处省略
broadcaster.sendTransform(static_transformStamped)

#重点是以下部分
x,y,z = 1,2,3
vector = [x,y,z]
v_base_link= [vector[0], vector[1],vector[2], 0] 
listener = tf.TransformListener()
loop_counter = 0
r = rospy.Rate(100)
while not rospy.is_shutdown():
    try:
        (trans,rot) = listener.lookupTransform('world', 'NED', rospy.Time(0))
        v_map = tf.transformations.quaternion_multiply(tf.transformations.quaternion_multiply(rot, v_base_link), tf.transformations.quaternion_conjugate(rot))
        v_new = v_map[0:3]
        if loop_counter > 100: #控制打印频率
            print(f"v_new:{v_new}")
            loop_counter = 0
        loop_counter += 1
    except Exception as e:
        print(f"Exception:{e}")
    r.sleep()

3. 启动roscore，source Python文件，rosrun 对应Python节点。
   具体过程略

结果

东北天坐标系下的[1,2,3]放在东北地坐标系下来表示就是[2,1,-3]。

打印结果如下图所示：

延伸阅读

四元数相比欧拉角的优势到底在哪里？

参考文献

略