索引就是排好序的数据结构，可以帮助我们快速的查找到数据，那么底层的数据到底是如何存储的呢？

为什么InnoDB 用的是B+tree 存储结构？

大家可以看看这个可视化的网站
数据结构和算法的可视化工具

可以看到数据结构里面有链表，二叉树，AVL，红黑树，Hash，B tree ，B+tree等等，可以点击进入每个数据结构的可视化页面，玩一玩，看看插入时数据是怎么样排序的

1.二叉查找树（Binary Search Trees）

二叉树的特点是左边节点比右边节点小，每个叶子节点下的子节点最多只能有2个，每次插入都会先比较根节点，小的往左边，大的往右边。

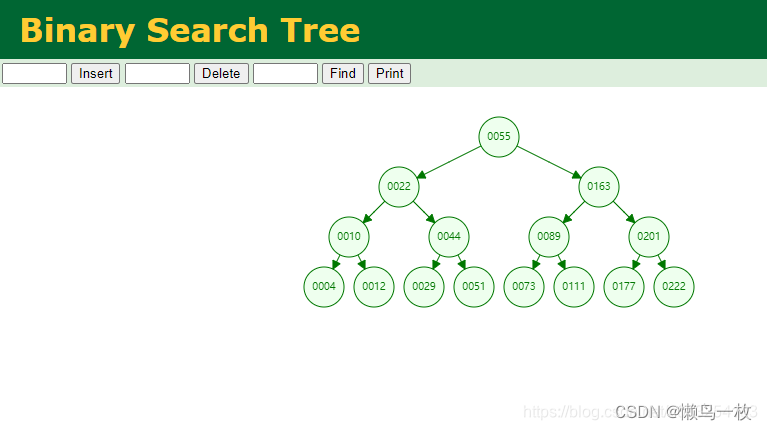
缺点
由于只能有2个叶子节点，所以数据量大的时候树的层级会非常高，而且当插入的数据都是有序的，如下图，就会造成斜树，这样就退化成有序链表了

2.平衡搜索二叉树（AVL trees）

解决了斜树的问题，每次插入是时候节点会进行旋转，左小右大，减少了树的高度，非叶子节点最多拥有2个叶子节点，同时树的左右2边层级 相差不会大于1；

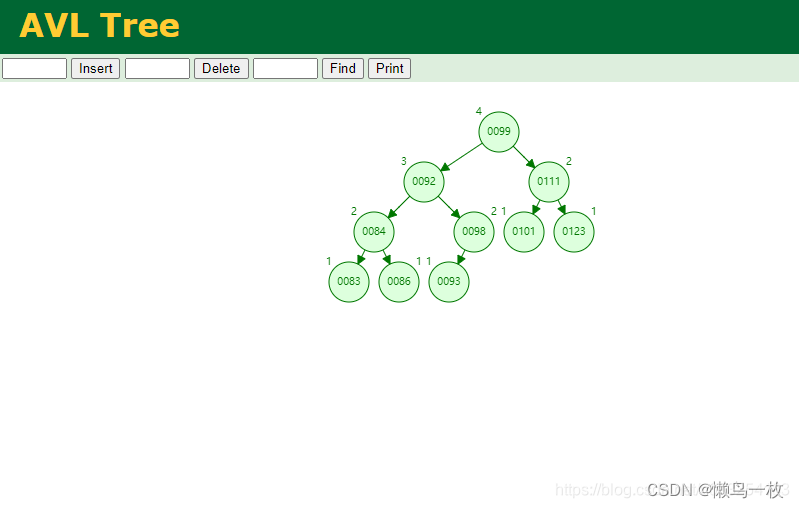
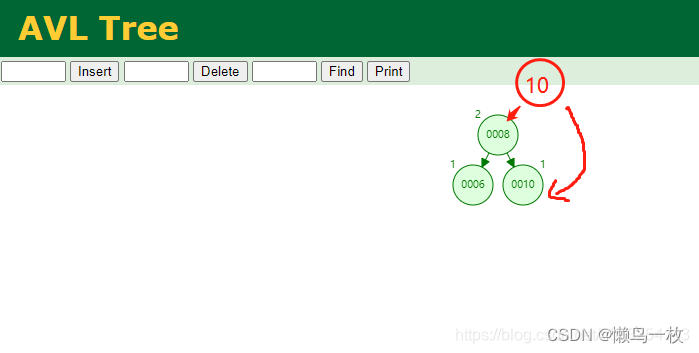
右旋LL：当想左边节的左子节点点插入数据，例如插入10，8，6的时候，为了保持树的平衡，会把10节点进行右旋，试树能够平衡

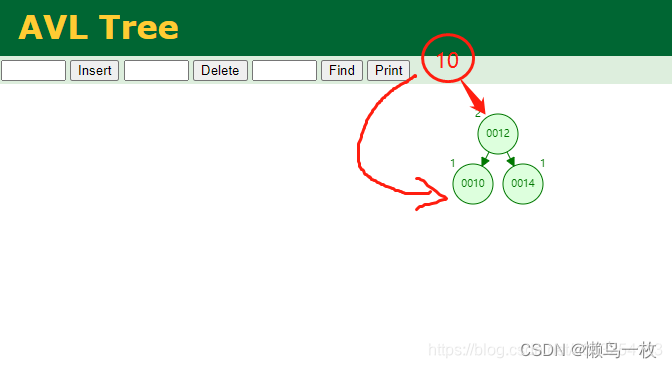
左旋RR：当想右边节的右子节点点插入数据，例如插入10，12，14的时候，为了保持树的平衡，会把10节点进行左旋，试树能够平衡

缺点
虽然解决了斜树的问题，但是还是会造成树的层级太高，每个叶子节点只能有2个子节点，查询的时候会造成IO次数太多

3.红黑树（Red-Black Trees）

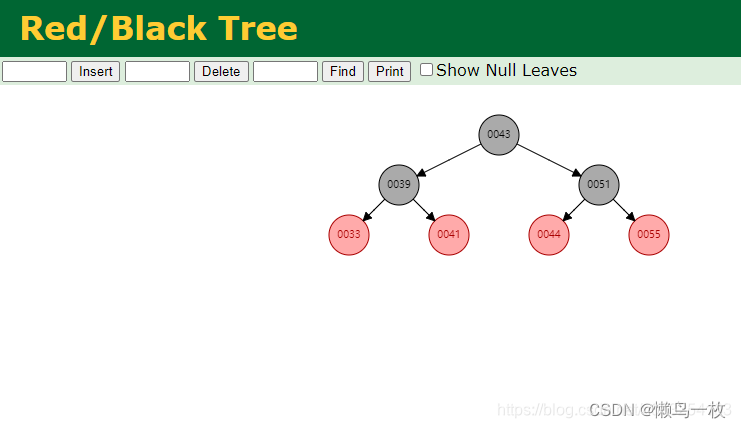
网上有大牛总结了个顺口溜：根节点必黑，新增是红色，只能黑连黑，不能红连红； 爸叔通红就变色，爸红叔黑就旋转，哪边黑往哪边转

缺点
红黑树的缺点是每个叶子节点只能有2个子节点，查询的时候会造成IO次数太多，同时树的层级会非常高

红黑树和AVL树的区别

• 红黑树不是完全平衡，不会像AVL那样要求左右2边节点的 绝对值差不大于1，它只要求部分达到平衡，但是提出了为节点增加颜色，红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决。
• AVL是完全平衡，在增加或者删除节点的时候，旋转的次数比红黑树要多。左右2边节点的 绝对值差不大于1。由于是完全平衡，所有查询效率要比红黑树高
• 复咋情况下，就是如有删除节点，树要回复平衡，红黑树的复衡效率更高，因为最多只需要旋转3次就能回复平衡，而AVL树可能会旋转多次，效率更低
• 在实际运用中，如果搜索的次数远远大于插入和删除，那么选择AVL，因为查询效率更高，如果搜索，插入删除次数几乎差不多，应该选择红黑树，因为维护效率更高。

4.Hash

Hash实际上是散列函数，它可以帮助我们大幅提升检索数据的效率，这是因为 Hash 只需要一步就可以找到对应的取值，算法复杂度为 O(1)。Hash 算法是通过某种确定性的算法（比如 MD5、SHA1、SHA2、SHA3）；

采用 Hash 进行检索效率非常高，例如查 id = 100的数据，基本上一次检索就可以找到数据，而 B+ 树需要自顶向下依次查找，多次访问节点才能找到数据，中间需要多次 I/O 操作，从效率来说 Hash 比 B+ 树更快。但是，hash 有很多缺点

缺点

• Hash 索引不能进行范围查询，例如id > 100就无法匹配索引
• Hash 索引不支持最左匹配原则，例如有联合索引 a_b_c_index，abc3个字段，Hash 索引在计算Hash 值的时候是将abc3个字段合并后再一起计算 Hash 值，不会针对每个索引单独计算 Hash 值。因此如果用到联合索引的一个或者几个索引时，联合索引无法匹配
• Hash 索引不支持 ORDER BY 排序
• 当数据量很大时，hash冲突的几率也会很是大，造成hash碰撞

5.B tree（多路平衡查找树）

上面讲到的树有个共同的缺点，就是每个叶子节点只能有2个子节点，这样的话都会造成树的层级太高，IO效率太低。

B-tree 利用了磁盘块的特性进行构建的树。每个磁盘块一个节点，每个节点包含了很关键字。把树的节点关键字增多后树的层级比原来的二叉树少了，这样就变成了N叉树，并且每个节点保存key和value和data，这样的存储方式的好处就是只要查询到对应数据的键值，就直接返回data，大大提高了查询效率，减少数据查找的次数和复杂度

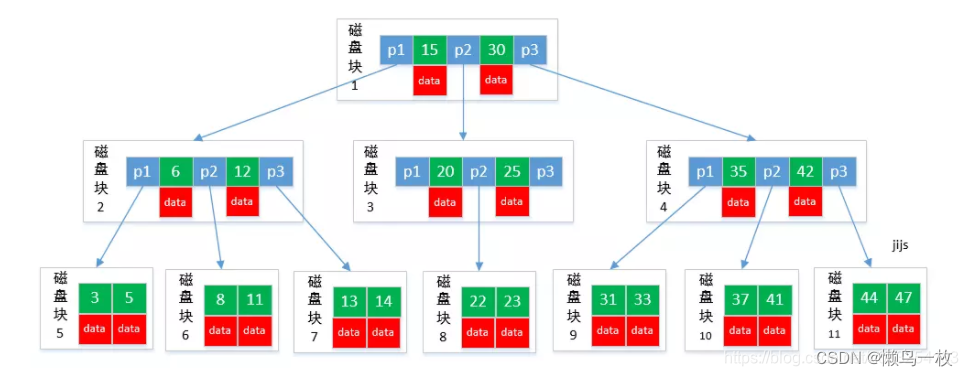
缺点
这样的存储结构有个缺点，就是由于每个节点都保存了key-value-data，那么一旦这个data的数据量大的话，例如这个数据有1k，10k或者更多，那么一个磁盘块（默认16KB）就无法保存这么多节点了，因为空间是有限的，保存不了的话就会生成子节点，这样的话树的高度又增加了，磁盘IO又多了，于是B树进行优化，就有了B+树

6.B+tree

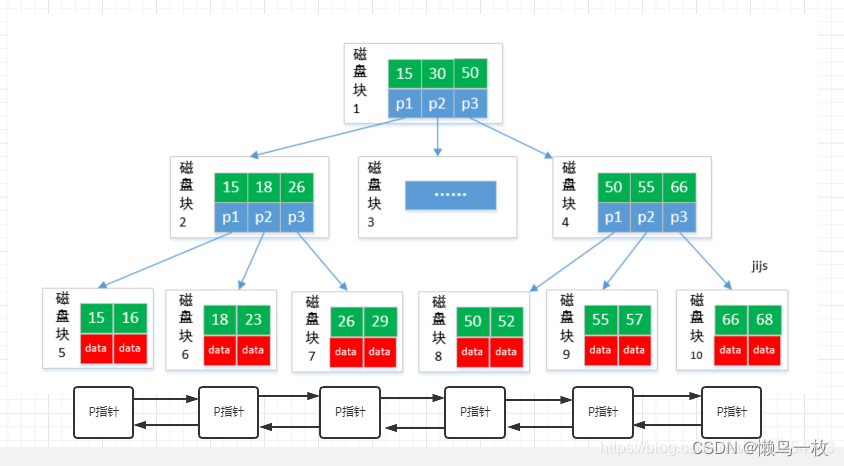
B+树和 B树最大的不同是非叶子节点只储存key和value信息，没有data，data 只保存在叶子节点上。这样做的好处是一个磁盘块可以存更多的节点，因为不需要存data了，树的高度就更矮了IO次数更低。

而且所有的叶子节点都是有序的双向链表，所有数据是按照顺序排列的，这样做的好处是范围查找，排序查找，分组查找的效率更高了，举个例子，例如查 23 < id < 52区间范围的数据，只需要找到23的这个数据，再通过有序链表，找到52，就可以快速的返回范围数据，减少了IO次数，提高查询效率

7.写在最后

总结了这么多，如果你还是不明白为什么要用B+tree做存储结构，那就再反复的学习吧