线性代数第一章行列式

news2024/9/23 5:38:54

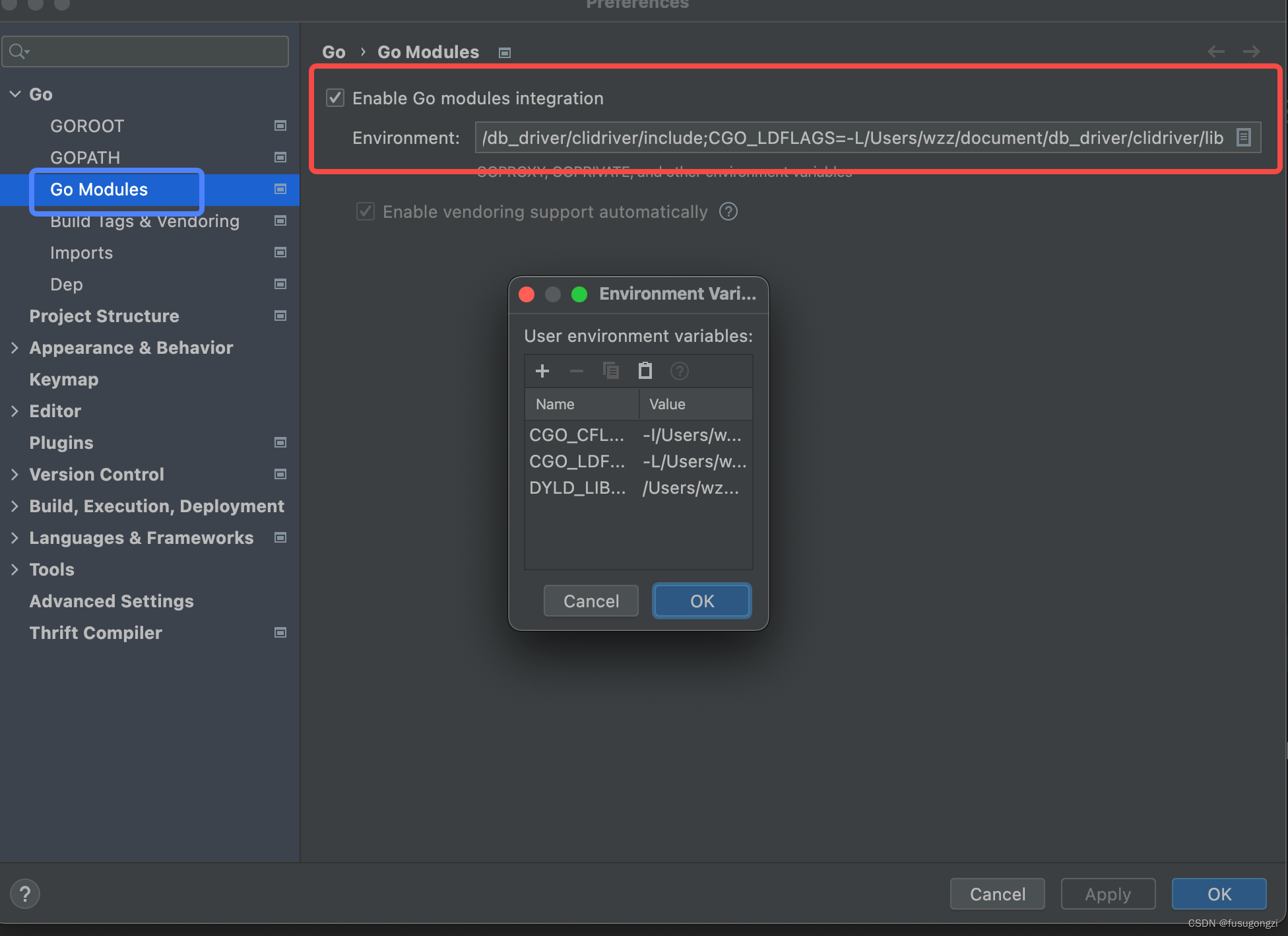
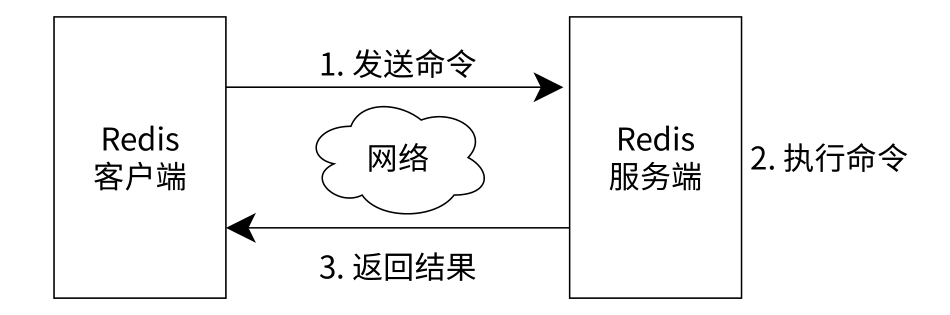
一、概念

不同行不同列元素乘积的代数和（共n!项）

二、性质

经转置行列式的值不变，即 $\left | A^T \right |=\left | A \right |$ ；
某行有公因数k，可把k提到行列式外。特别地，某行元素全为0，则行列式的值为0；
两行互换行列式变号，特别地，两行相等行列式值为0，两行成比例行列式值为0；
某行所有元素都是两个数的和，则可写成两个行列式之和；
某行的k倍加至另一行，行列式的值不变。

三、展开式

|A|=ai1Ai1+ai2Ai2＋…+ainAin（按i行展开）

|A|=a1jA1j+a2A2j+…＋anjAnj（按j列展开）

四、计算

4.1 数字型

三角化法、公式法、归纳法

常用技巧

直接按行（列）展开
把第1行（列）的k倍加到第i行（列）
把每行（列）都加到第1行（列）
逐行（列）相加

4.2 抽象型

用行列式性质
用矩阵性质
用特征值 $\left | A \right |=\prod \lambda _i$ 相似

五、证 $\left | A \right |=0$

$Ax=0$ 有非零解
反证法
$r(A)<n$
0是A的特征值
$\left | A \right |=-\left | A \right |$

设某系数行列式为D

D≠0，非齐次线性方程组有唯一解；D=0，可能无穷多解，也可能无解。

D≠0，齐次线性方程组只有零解；D=0，有非零解（即无穷多解）。

六、应用

$Ax=0$ 有非零解
伴随矩阵求逆法
线性相关（无关）判定
可逆的证明
克拉默法则
特征值计算
二次型正定判定

七、主要公式

上（下）三角行列式的值等于主对角线元素的乘积
关于副对角线的行列式 $=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2,n-1}...a_{n1}$
两个特殊的拉普拉斯展开式主对角线 $\left | A \right |\cdot \left | B \right |$ 副对角线 $(-1)^{mn}\left | A \right |\cdot \left | B \right |$
范德蒙行列式 $=\prod_{1\leqslant j< i\leqslant n}(x_i-x_j)$
特征多项式

设A是3阶矩阵，则A的特征多项式 $\left | \lambda E-A \right |=\lambda ^{3}-(a_{11}+a_{22}+a_{33})\lambda ^{2}+s_2\lambda -\left | A \right |$

其中

$s_2=\left | \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right | + \left | \begin{array}{ccc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right | + \left | \begin{array}{ccc} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right |$