一、最优状态值函数

        解决强化学习任务大致上意味着找到一种政策，能够在长期内实现很多奖励。对于有限MDPs，我们可以精确地定义一种最优政策，其定义如下。值函数定义了政策的一种部分排序。如果一个政策的预期回报大于或等于另一个政策π0在所有状态下的预期回报，则称该政策π优于或等于π0。换句话说，如果对于所有的s ∈ S，vπ(s) ≥ vπ0(s)，则π ≥ π0。总是存在至少一个政策优于或等于所有其他政策，这就是最优政策。虽然可能存在多个最优政策，但我们用π∗表示所有最优政策。它们具有相同的状态值函数，称为最优状态值函数，记作v∗，定义为

        最优政策也具有相同的最优动作值函数，记作q∗，其定义如下。

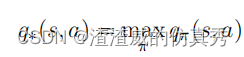
        对于所有的 s ∈ S 和 a ∈ A(s)，此函数为 (s, a) 状态动作对应提供采取动作 a 在状态 s 中并此后遵循最优策略的预期回报。因此，我们可以将 q∗ 表示为 v∗ 的函数，如下所示：

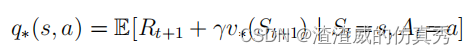
二、高尔夫球示例中的最优状态值函数

        高尔夫球示例图的下半部分显示了可能的最佳动作值函数q∗(s, driver)的等高线。 这些是每个状态的值，如果我们首先用driver击球，然后选择driver或putter，哪个更好。 driver可以让我们把球击得更远，但精度较低。 如果我们已经非常接近，那么我们只能使用driver一杆将球打入洞中；因此q∗(s, driver)的e1等高线仅覆盖绿地的很小一部分。 然而，如果有两次击球，那么我们可以从更远的地方到达洞穴，如e2等高线所示。 在这种情况下，我们不必一路开车到小l1等高线内，而只需在绿地上任何地方；从那里我们可以使用putter。 最佳动作值函数给出了在执行特定第一个动作后得到的值，在这种情况下是driver，但随后使用最佳动作。 e3等高线更远，包括起始发球台。 从发球台开始，最佳动作序列是两次驱动和一次推杆，三杆将球击入洞中。 因为v∗是政策的值函数，所以它必须满足贝尔曼方程对于状态值的自洽条件。 因为它是最优值函数，所以v∗的一致性条件可以以特殊形式写入而不参考任何特定策略。这是贝尔曼方程对于v∗或贝尔曼最优方程。 直观地说，贝尔曼最优方程表示在最优策略下状态的值必须等于从该状态出发的最佳动作的预期回报。

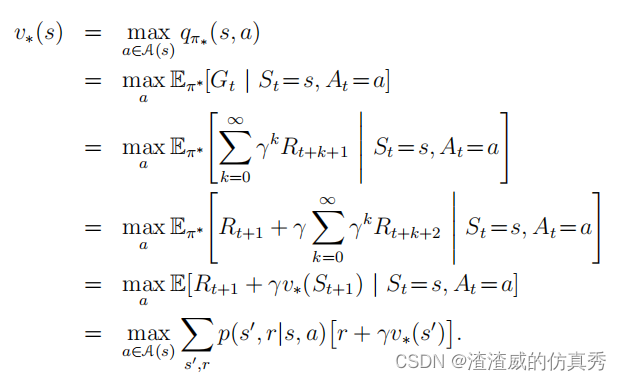
最后两个方程是v∗的贝尔曼最优方程的两种形式。q∗的贝尔曼最优方程为

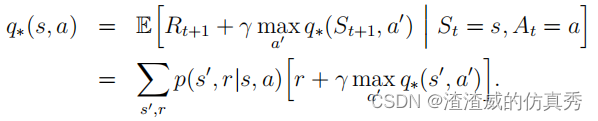
        图1以图形方式显示了贝尔曼最优方程中考虑的未来状态和动作的范围。 这些与vπ和qπ的备份图相同，只是在代理的选择点处增加了弧线，以表示在该选择上的最大值，而不是给定某个策略的预期值。 图1a以图形方式表示了贝尔曼最优方程。 对于有限MDPs，贝尔曼最优方程具有独立于策略的唯一解。 实际上，贝尔曼最优方程是一个方程系统，每个状态一个方程，因此如果有N个状态，则有N个方程和N个未知数。 如果知道环境动态（p(s0, r|s, a)），则原则上可以使用解决非线性方程的各种方法中的任何一种来解决这个方程系统以获取v∗。 可以解决一组相关的方程以获取q∗。
        一旦获得了v∗，确定最优策略就相对容易了。 对于每个状态s，贝尔曼最优方程中都将获得一个或多个动作的最大值。 任何仅将这些动作指定为非零概率的策略都是最优策略。 您可以将此视为单步搜索。 如果您拥有最优价值函数v∗，则单步搜索后出现的最佳动作将是最佳动作。 另一种说法是，任何相对于最优评估函数v∗的策略都是贪婪策略。 在计算机科学中，贪婪一词用于描述仅基于本地或即时因素选择选项而不考虑这种选择可能阻止未来访问更好替代方案的搜索或决策过程。 因此，它描述了仅基于短期后果选择动作的策略。

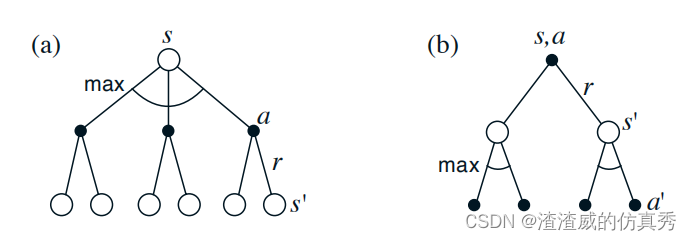
图1

        v∗的美妙之处在于，如果用它来评估行动的短期后果，特别是单步后果，那么在长期意义上，贪婪策略实际上是最优的，因为v∗已经考虑到了所有可能未来行为的奖赏后果。通过v∗，最优的预期长期回报被转化为一个对每个状态来说是局部和立即可用的数量。因此，一步超前搜索产生了长期的最佳行动。

        拥有q∗使选择最佳行动更加容易。有了q∗，代理甚至不需要进行一步超前搜索：对于任何状态s，它可以简单地找到最大化q∗(s, a)的任何行动。动作值函数有效地缓存了所有一步超前搜索的结果。它为每个状态-动作对提供了最优的预期长期回报，而这是局部和立即可用的值。因此，在表示状态-动作对的函数的代价下，而不是仅仅表示状态，最优的动作值函数允许选择最佳行动，而不必知道可能的后续状态及其价值，也就是说，不必知道环境的动态。