【算法练习Day33】不同路径不同路径 II

news2024/12/26 9:20:22

在这里插入图片描述

📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：练题
🎯长路漫漫浩浩，万事皆有期待

文章目录

不同路径
不同路径 II
总结：

本期是两道路径题目，也是用来练习动态规划的好题目，但是我认为没有做过的话还是不太容易想出思路的。

不同路径

62. 不同路径 - 力扣（LeetCode）
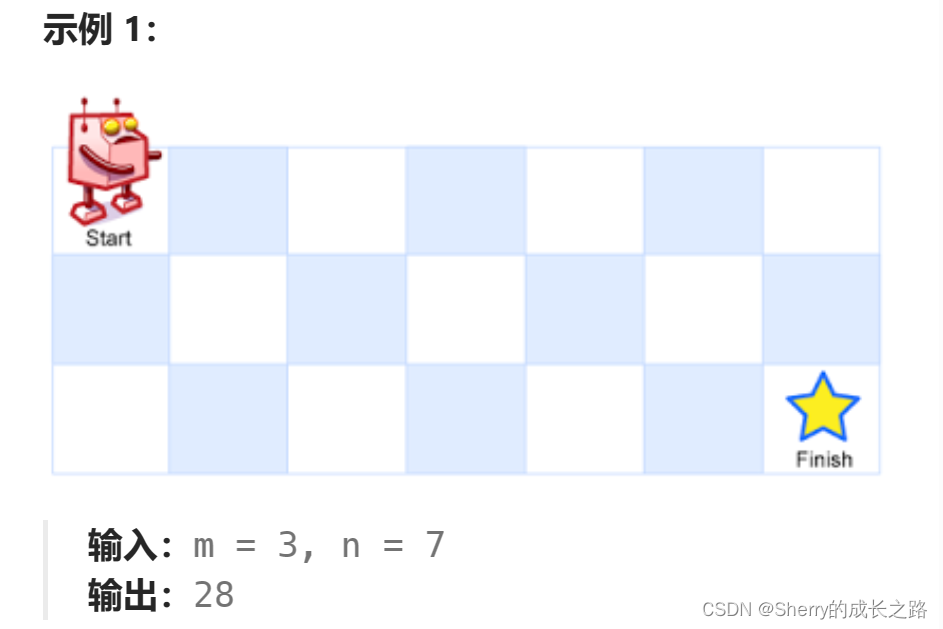
在这里插入图片描述

分析题目，要求的是从起始点start到达目的地的不同路径共有几条，分析题意可知，起始点每次都是左上角的顶点，而且机器人每次只能向右前进或者向下前进，不能往回走，这一点十分重要，也就是说该机器人一直向右前进或者一直向下前进，只有一种方案可以到达。这一点很重要，我们根据这一特性来设计动态规划里的dp数组，然后进而推出其他的方格。

dp数组的含义：dp[i][j]代表了当前所处方格处共有多少种方法可以到达此处，i和j是行和列的下标

dp数组初始化：根据之前的分析，我们可以知道将最上边一行和最左侧一列都初始化为1，是合适的。因为到达它们的路径仅有一条。

递推公式：递推公式的得来是根据推理而得出的。我们知道机器人一次只能向下面或者向右边移动一格，那么到达当前的方格的路径数很显然就是该方格上面的位置的路径数加上该方格左边位置的路径数，它们的和也就是当前方格的路径数，公式写成dp[i][j]=dp[i][j-1]+dp[i-1][j]

遍历顺序：这里很显然是从左向右，从上向下，因为我们最终是从左上角出发到达右下角。

通过上述的分析，我们可以得到以下代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>>dp(m,vector<int>(n,0));
        for(int i=0;i<m;i++)
        {
            dp[i][0]=1;
        }
        for(int j=0;j<n;j++)
        {
            dp[0][j]=1;
        }
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

关于递推公式如果有不理解的地方，在纸上模拟是最好的方法，我们可以将该二维数组想象成行列均为2，这样很容易知道从起点到终点确实是两种方法。而这两种方法和我们分析的上左两位置路径和的相加即为正确答案的思路，完全相符合。

不同路径 II

63. 不同路径 II - 力扣（LeetCode）
在这里插入图片描述

这道不同路径2和上一道题比，仅仅是多了障碍物这一设定，机器人不能走到放了障碍物的方格上，这里的代码和上一道题差不多，但是一定要注意，障碍物不仅可能出现在中间部分，甚至在初始化时候，也就是最上面一行和最左侧一列也是可能出现的，这一点一定要注意，不要让机器人踩到障碍物上。

dp数组及其含义：仍然是代表了此方格的路径总数

dp数组初始化：初始化时，还是将最上一行和最左一列初始化为1，但是遇到障碍物后，不再进行该行或列的初始化，因为机器人不能向后走的缘故，这些方格永远不会达到。

递推公式：同上一题

遍历顺序：也同上一题

仅仅是需要注意障碍物的问题，如果初始化时候遇到障碍物，那么该行或者列不进行初始化，如果在递推求其他方格时候出现障碍物，则跳过该障碍物方格。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) 
    {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector<vector<int>>dp(m,vector<int>(n,0));
        for(int i=0;i<m&&obstacleGrid[i][0]==0;i++)
        {
            dp[i][0]=1;
        }
        for(int j=0;j<n&&obstacleGrid[0][j]==0;j++)
        {
            dp[0][j]=1;
        }
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(obstacleGrid[i][j]==1)continue;
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};