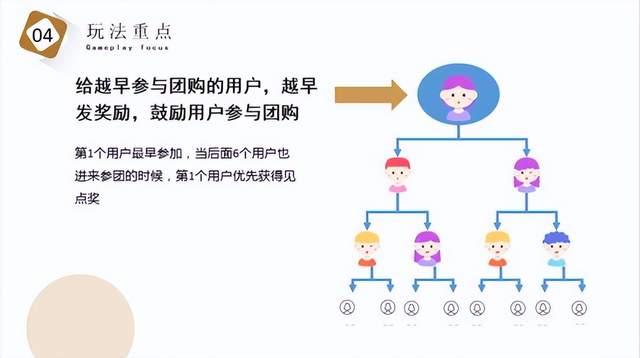
论文地址:https://export.arxiv.org/pdf/1904.05049
代码地址:https://gitcode.com/mirrors/lxtgh/octaveconv_pytorch/overview?utm_source=csdn_github_accelerator
1.是什么?
OctaveNet网络属于paper《Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution》,是CVPR2019中的一篇论文。
Octave Convolution是一种用于卷积神经网络的新型卷积操作,旨在减少卷积神经网络中的空间冗余。它通过将输入特征图分成高频和低频两个部分,然后在这两个部分上执行不同的卷积操作,从而实现减少计算量和内存占用的目的。Octave Convolution的主要思想是将高频和低频特征图分开处理,以便更好地利用它们的特性。这种方法可以在不损失精度的情况下减少计算量和内存占用,从而提高卷积神经网络的效率。
2.为什么
从频域的角度理解图像
我们都知道,一副图像从空间域的角度看,它一般情况下是一个3 × W × H 3 \times W \times H3×W×H的矩阵,矩阵中每一个位置都有一个[0,255]的值,而从频域的角度出发的话,一副图像都可以被分解为描述平稳变化结构的低空间频率分量(低频域、low-frequency)和描述快速变化的精细细节的高空间频率分量(高频域、high-frequency),就像下面这幅图:
最左侧为原始图像,中间为低频的部分,它比较多的反应的是图像的整体信息,最右侧为高频部分,它更多的反应图像的细节信息,比如边缘。这就好比空间域下的梯度,图像中存在边缘的地方,往往就是梯度大的地方。
特征图的高频与低频表示
既然对于图像来说可以区分高频与低频,那么对于特征图也是这样,特征图无非就是一个channel更多的矩阵而已,但是对于一个端对端的CNN模型,总不能在网络中引入一种频域计算,所以Octave Convolution显示的定义了“下采样”操作后的特征图叫做“低频域”,而不做下采样的原始尺寸叫做“高频域”。这样一来由于下采样带来的特征图尺寸减小,从而使得Octave Convolution计算量降低,此外网络有了不同尺度的信息(两个频域),并且两个频域的信息会在卷积完成后聚合,这个特性使得Octave Convolution具有比之前更好的性能。“下采样”的scale,采用的是2的幂次,而目前文章只讨论了2 的1 次幂的情况,说白了就是特征图的长宽都缩小了2,就像下面这张图:

图(b)是一个原始的特征图,并人为的切分特征图为Low Frequency和High Frequency,切分的标准是0.25,0.5,0.75三个系数,比如一个channel=64的特征图,系数为0.5的情况下,那么32个通道为低频,另外32个为高频。图©是用下采样操作实现低频域,就是上面说到缩小2倍。图(d)想要说明这个低频和高频要通过卷积做update,然后还有聚合交换的部分,反正只看(d)是看不出来,后面再具体介绍。
在这里不得不吐槽一点,论文由图像引出了高频和低频,但是到了卷积的地方直接过渡到了“下采样”,此后low-frequency和high-frequency还一直贯穿全文,这给人一种写论文写的过劲的感觉,毕竟Low Frequency、High Frequency和Octave 要比upsample和subsample好听,但是其实就是下采样完了上采样,尤其是我们要去实现它的时候。
3.怎么样?
3.1网络结构图
一个特征图的通道数根据预设系数
切分为高频
与低频
的部分,低频部分的宽高都缩小为原来的一半。然后Octave Convolution会做下面四个部分
(1)高频部分直接卷积:,即高频到高频的卷积,输出通道数
(2)高频部分先做下采样再卷积,这里的下采样是,然后
,即高频到低频的卷积,输出通道数
(3)低频部分直接卷积后做上采样:,这里的 upsample
所用的上采样方法我们后面再说,即低频到高频的卷积,输出通道数
(4)低频部分直接卷积:,即低频到低频的卷积,输出通道数
这四个部分完成之后,接下来就要做信息的聚合,也就是(1)和(3)的结果做一个对应位置的按位加操作,(2)和(4)的结果做一个对应位置的按位加操作。
这样Octave Convolution就完成了,它其实在做的就是把原来的一个卷积操作,拆成了4个,而这4个中有三个处理的输入都是原来特征图w,h的一半,所以计算量就下来了。
3.2代码实现
class OctaveConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, alpha_in=0.5, alpha_out=0.5, stride=1, padding=1, dilation=1,
groups=1, bias=False, up_kwargs = up_kwargs):
super(OctaveConv, self).__init__()
self.weights = nn.Parameter(torch.Tensor(out_channels, in_channels, kernel_size[0], kernel_size[1]))
self.stride = stride
self.padding = padding
self.dilation = dilation
self.groups = groups
if bias:
self.bias = nn.Parameter(torch.Tensor(out_channels))
else:
self.bias = torch.zeros(out_channels).cuda()
self.up_kwargs = up_kwargs
self.h2g_pool = nn.AvgPool2d(kernel_size=(2,2), stride=2)
self.in_channels = in_channels
self.out_channels = out_channels
self.alpha_in = alpha_in
self.alpha_out = alpha_out
def forward(self, x):
X_h, X_l = x
if self.stride ==2:
X_h, X_l = self.h2g_pool(X_h), self.h2g_pool(X_l)
X_h2l = self.h2g_pool(X_h)
end_h_x = int(self.in_channels*(1- self.alpha_in))
end_h_y = int(self.out_channels*(1- self.alpha_out))
X_h2h = F.conv2d(X_h, self.weights[0:end_h_y, 0:end_h_x, :,:], self.bias[0:end_h_y], 1,
self.padding, self.dilation, self.groups)
X_l2l = F.conv2d(X_l, self.weights[end_h_y:, end_h_x:, :,:], self.bias[end_h_y:], 1,
self.padding, self.dilation, self.groups)
X_h2l = F.conv2d(X_h2l, self.weights[end_h_y:, 0: end_h_x, :,:], self.bias[end_h_y:], 1,
self.padding, self.dilation, self.groups)
X_l2h = F.conv2d(X_l, self.weights[0:end_h_y, end_h_x:, :,:], self.bias[0:end_h_y], 1,
self.padding, self.dilation, self.groups)
X_l2h = F.upsample(X_l2h, scale_factor=2, **self.up_kwargs)
X_h = X_h2h + X_l2h
X_l = X_l2l + X_h2l
return X_h, X_l
参考:
Octave Convolution 代码详解
『深度概念』一文读懂Octave Convolution(OctConv)八度卷积
Octave Convolution原理与Caffe实现