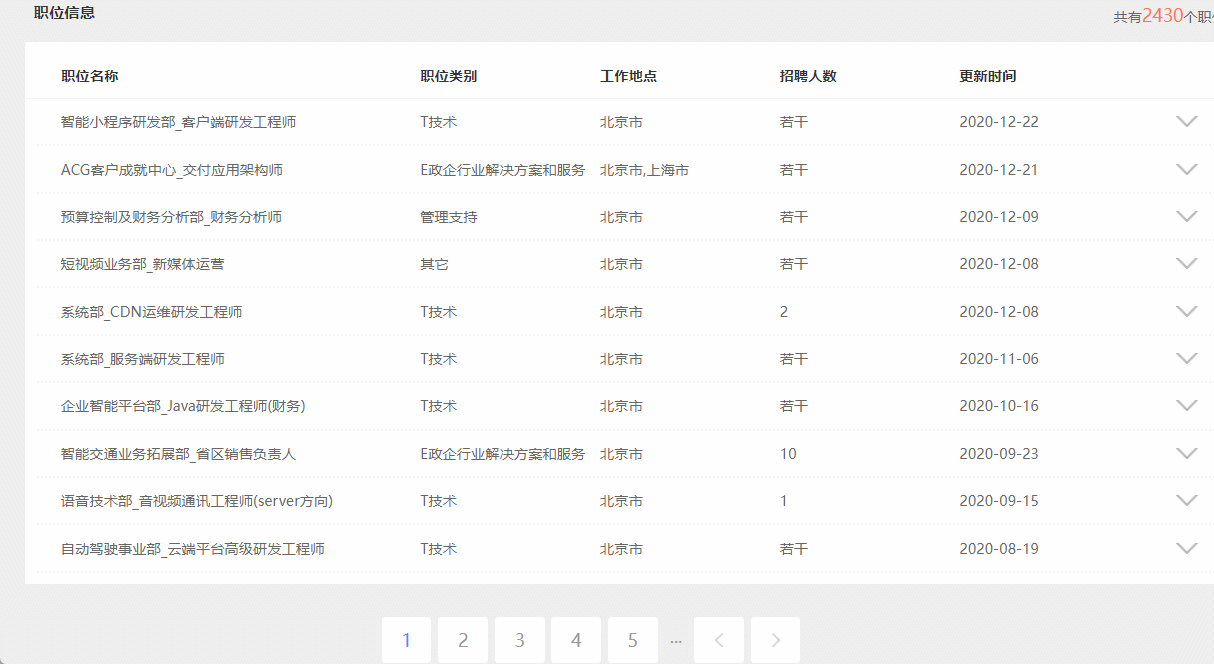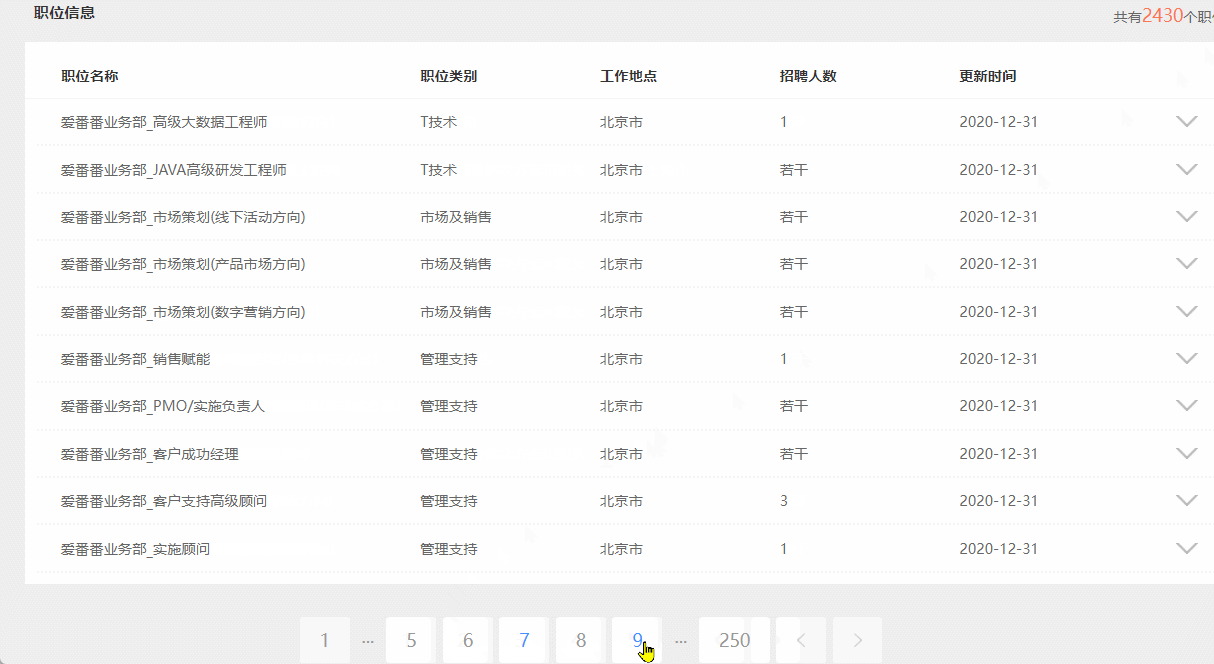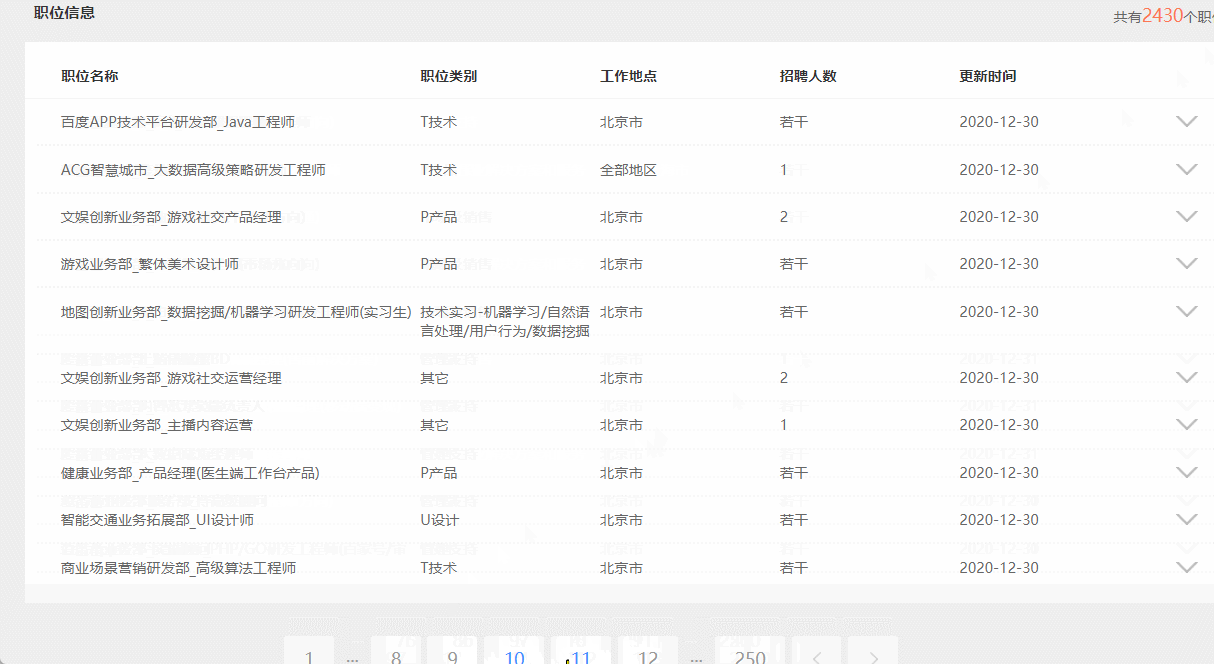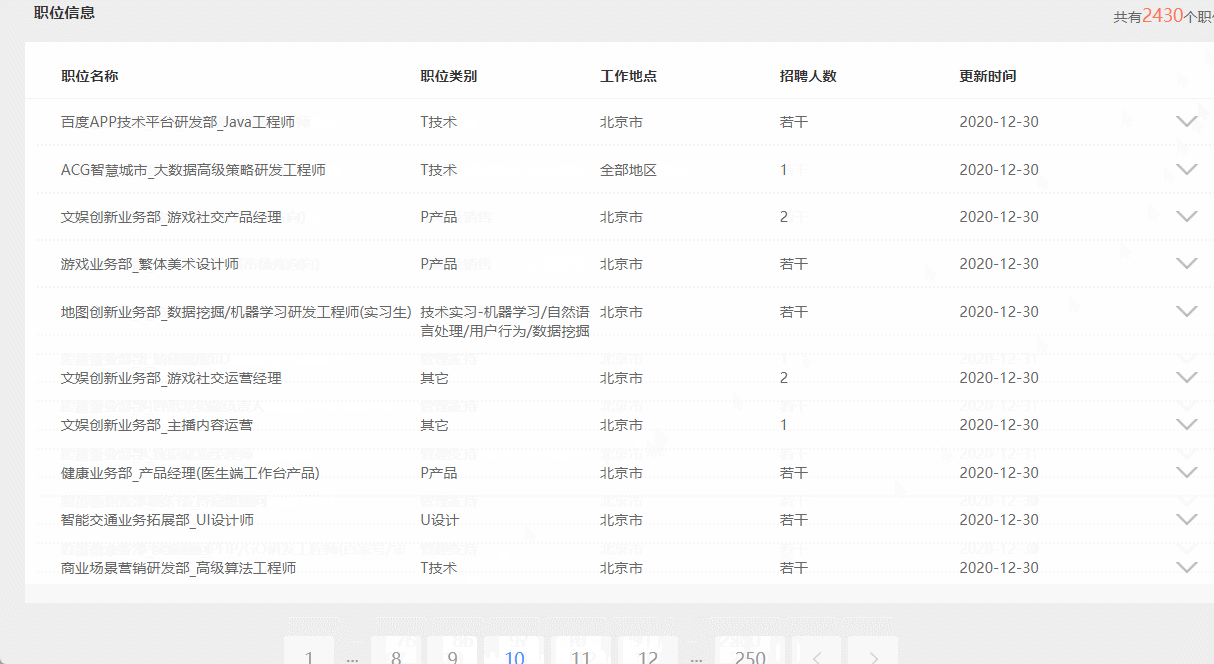
概念
优先级队列是啥？
堆是啥？
优先级队列的底层运用到堆这种数据结构
堆的特点：总是一棵完全二叉树
大根堆：
每一棵树的根结点总是比左右子节点大
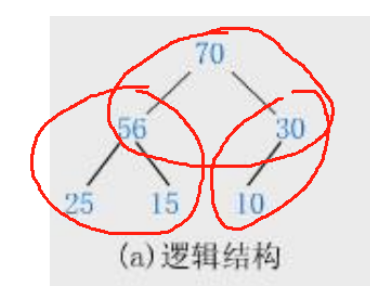
小根堆：
每一棵树的根结点的值总是比左右子节点小，不考虑左右子节点谁大谁小
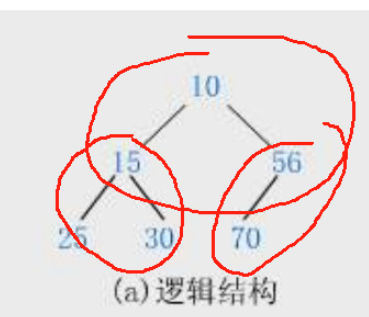
堆的存储
存储方式采用层序遍历的方式把二叉树的元素一一放到数组里面
那数组可不可以存储非完全二叉树呢？答案是可以的，但是会有空间浪费的情况
像上面右边图，4的位置没有存储元素，这就是一种空间浪费
来手搓一个堆
回顾一下二叉树里面性质的第五点
如何将普通数组转换成堆
把下面数组的元素画成堆
先画成一棵普通的二叉树
画成大根堆
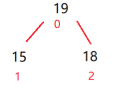
28<37，互换。最左边子树49>25>18，把49变成该树的根结点，最右边的树65>34>19，也进行交换
调整第二层的树，49>15>37，49作为根，而15<18<25，下方的树得把25变成根
最上面一层的树，65>49>27，65做根结点，而27<34，所以34还得作为该子树的根结点
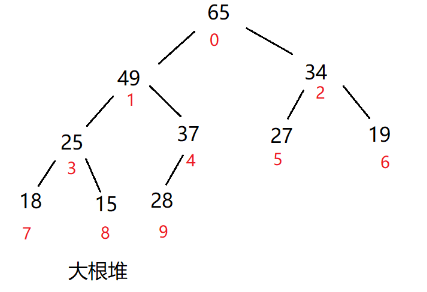这就是一个大根堆了
总结：
1.从最后一棵子树开始调整
2.在要变换的树里面，从左右孩子里面找到最大的与根结点比较，大了就进行互换
3.如果能够知道子树根结点下标，那么下一棵子树就是当前根结点下标-1
4.一直调整到0下标这个树为止
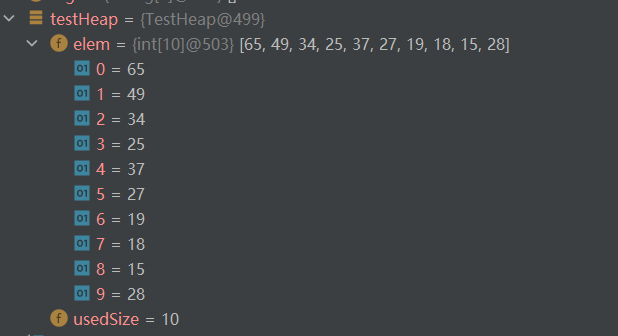
先写个初步的代码
public class TestHeap {
private int[] elem;
public int usedSize;//记录当前堆当中有效的数据个数
public TestHeap(){
this.elem = new int[10];
}
//存储数组
public void initElem(int[] array){
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
usedSize++;
}
}
问题
1.最后一棵子树根结点下标是多少
因为i = len-1，所以根结点index = (i-1)/2
public void createHeap(){
//usedSize-1相当于最后一棵树孩子结点的下标i，再-1是为了求父结点
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
siftDown(parent,usedSize);
}
}
2.每棵子树调整完之后，结束的位置怎么定？也就是我要从哪里开始调整下一棵子树？
我们采用向下调整的方法（注意，虽然我们是从最后一颗树往根结点方向调整，但是每一棵树的处理我们还是采用从父结点到子节点的调整方法。为什么用不向上调整？后面我会说到。）
找到最后一个元素置为c，其根结点为p
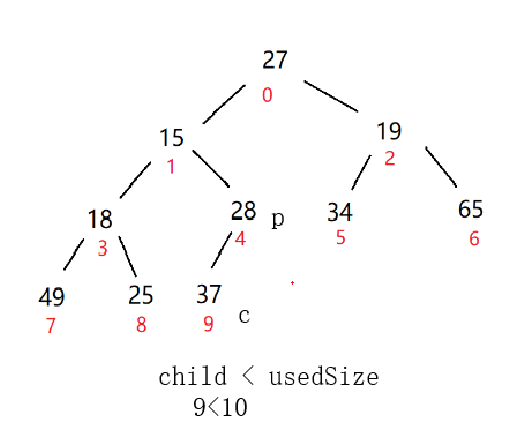
调整完后不知道下面还有没有元素要调整，所以c还得往下走
此时c的坐标是19 > 10了，所以可以停止了
private void siftDown(int parent, int len){
int child = 2 * parent + 1;
while(child < len){
//左右孩子比较大小
if(elem[child] < elem[child + 1]){
child = child + 1;
}
//走完上面的if，证明child下标一定是左右两个孩子最大值的下标
}
}现在问题来了，写到这里会发生数组越界，如果我的child移到9下标这里，那这个if判断elem[child] < elem[child+1] 这里的child+1 = 10 = usedSize，而这棵树根本就没有10这个下标，造成了越界
修改一下代码
if(child+1<len && elem[child] < elem[child + 1]){
child = child + 1;
}后面就是比较孩子和父结点的代码了
/**
* 向下调整
* @param parent
* @param len
*/
private void siftDown(int parent, int len){
int child = 2 * parent + 1;
while(child < len){
//左右孩子比较大小
if(child+1<len && elem[child] < elem[child + 1]){
child = child + 1;
}
//走完上面的if，证明child下标一定是左右两个孩子最大值的下标
if(elem[child] > elem[parent]){
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child;
child = 2 * parent + 1;
}else{
break;//不用比不用调了
}
}
}测试一下，没有问题😊
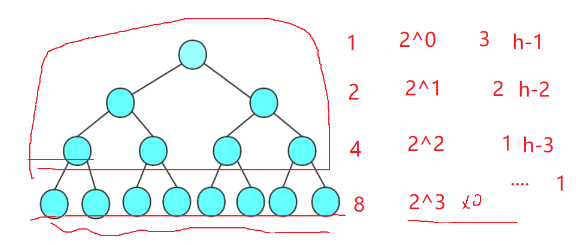
怎么计算这个堆的时间复杂度？
考虑最坏情况，就是满二叉树的情况
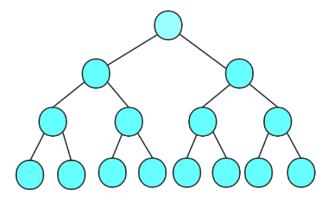
首先明确一点，最后一层结点时不进行调整的，一般是从倒数第二层结点开始调整的
设树的高度是h
T(N) = (h-1)*2^0+(h-2)*2^1+(h-3)*2^2+......+2*2^(h-3)+1*2^(h-2)
怎么求这个等式？采用错位相减
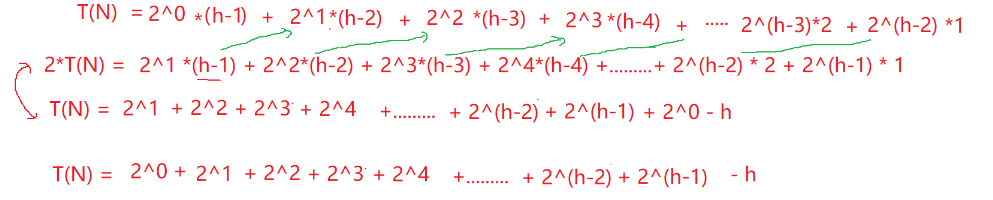
根据等比求和公式
T(n) = 2 ^ h - 1 - h
因为n=2^h-1 --> h = log(n+1)
代进去T(n) = n - log(n+1)
因为log(n+1)的图长这样，n越大越趋于一个常数
所以整个等式占支配地位的还得是n，所以T(N) ≈ n -->时间复杂度：O(N)
堆的插入
如果插入的数值比较小
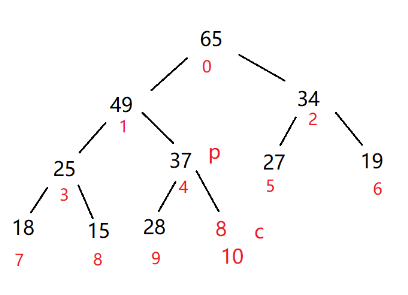
如果插入的数值比较大，那就得一层一层进行调整
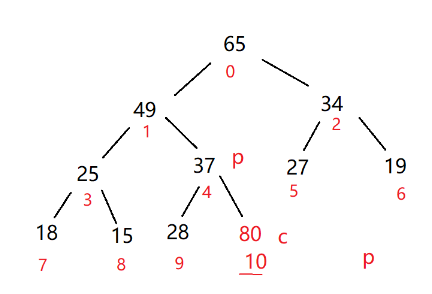
这种调整叫做向上调整
public void swap(int i, int j){
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
public void push(int val){
if(isFull()){
elem = Arrays.copyOf(elem, 2*elem.length);
}
elem[usedSize] = val;
//向上调整
siftUp(usedSize);
usedSize++;
}
//判断满不满
public boolean isFull(){
return usedSize == elem.length;
}
public void siftUp(int child){
int parent = (child - 1) / 2;
while(child>0){
if(elem[child] > elem[parent]){
swap(child,parent);
child = parent;
parent = (child - 1) / 2;
}else{
break;
}
}
}在测试里面把80push进去，没有问题😊
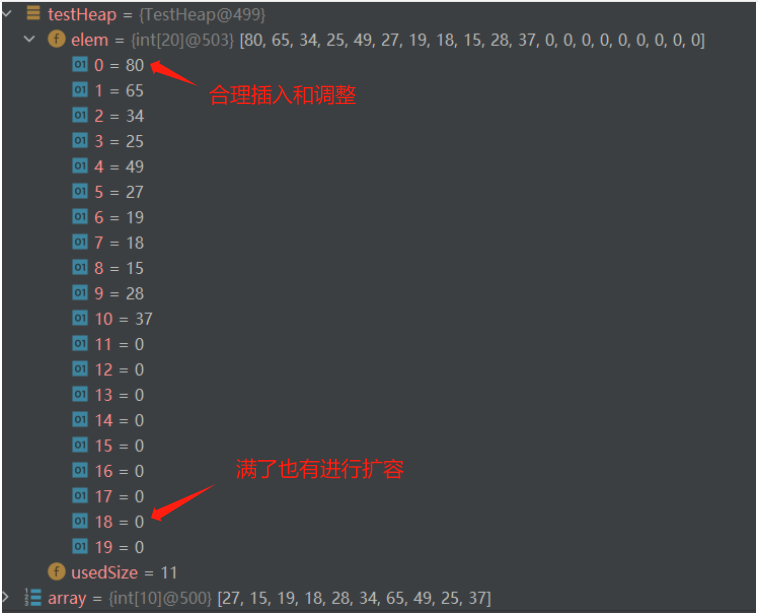
堆的插入的时间复杂度
因为最坏情况插入的元素是最大的，那这个元素最多也就向上调整到根节点的位置，也就是h
复杂度就是O(logN）
欸那为什么不用向上调整来建堆呢？😐
我们分析一下，拿这棵满二叉树来说，最底层有8个元素，已经占了一半了，网上建堆得每个元素都遍历一遍，时间复杂度太大了
堆的删除
因为堆的删除一定是删除优先级最高的值，所以一定是删除大根堆的根结点
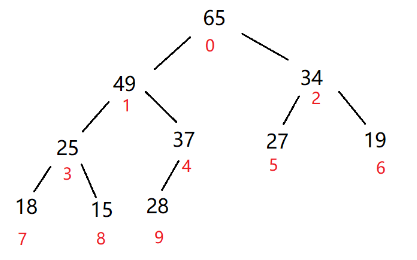比如这个，我们要做的就是删除65
第一步：把65（0下标）与28（最后一个元素）进行交换
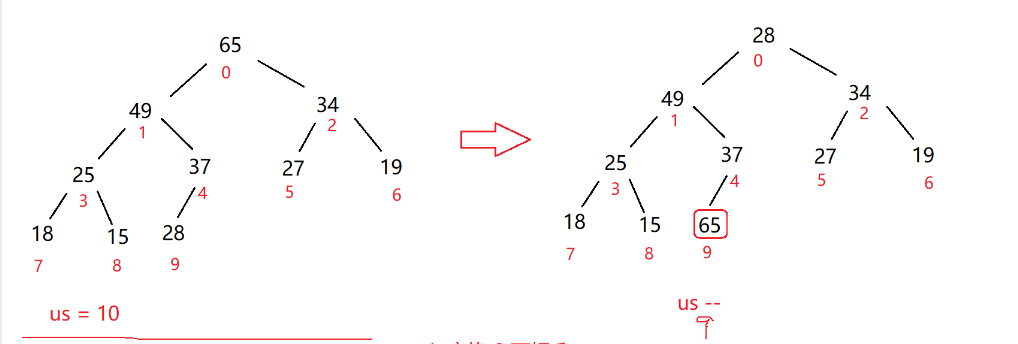
第二步：向下调整0下标
public int pop(){
if(empty()){
throw new EmptyException("数组空了！");
}
int oldVal = elem[0];
swap(0,usedSize-1);
usedSize--;
siftDown(0,usedSize);
return oldVal;
}
public boolean empty(){
return usedSize == 0;
}测试一下，没有问题😊
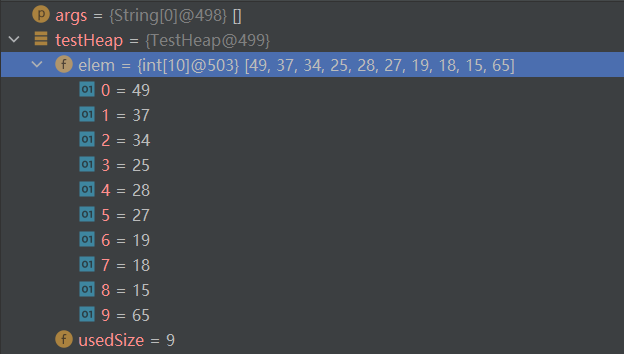
习题：
选A（可以自己画图，反正就是层序遍历画树）
选C
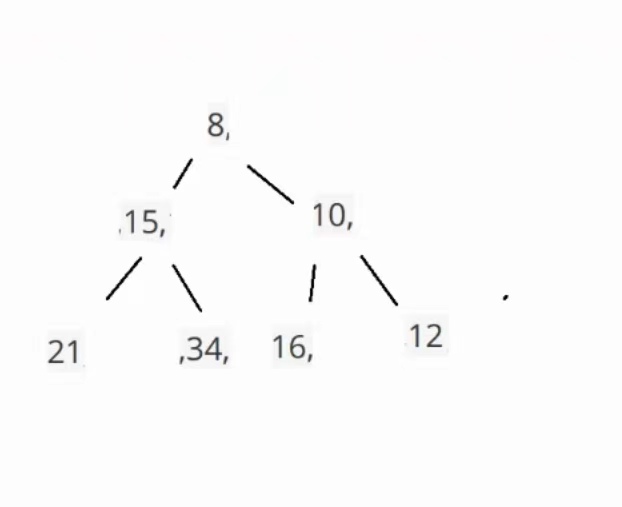
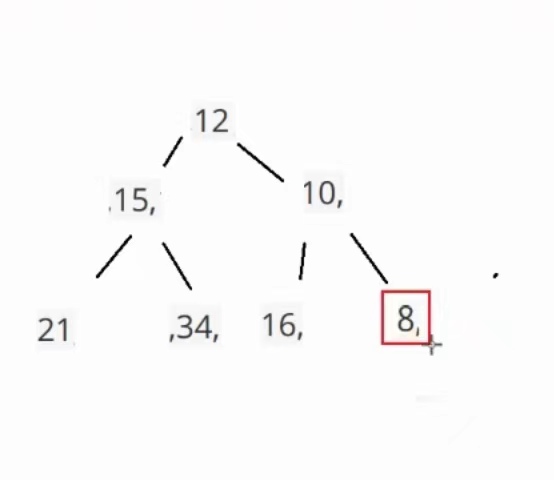
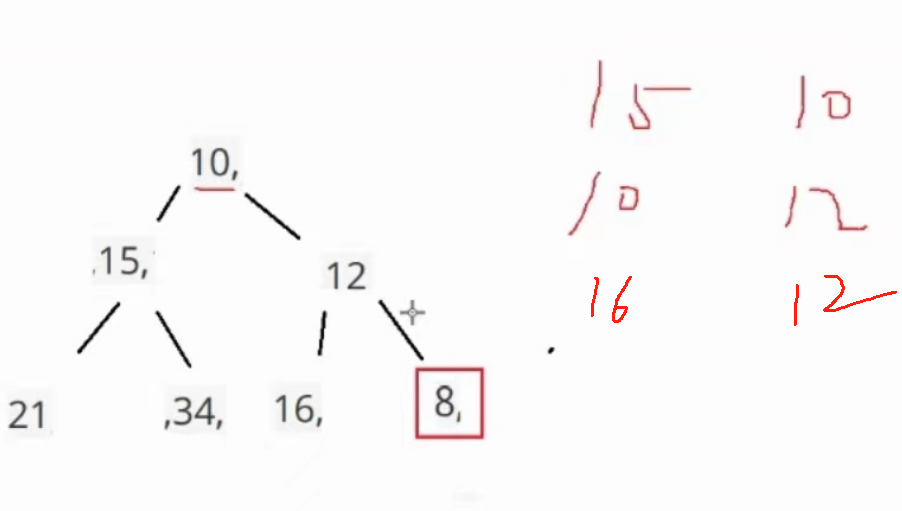
总共比较3次，左边那个15的原本就是小根堆，所以就不用比较
PriorityQueue
Java集合框架提供了PriorityQueue的优先级队列
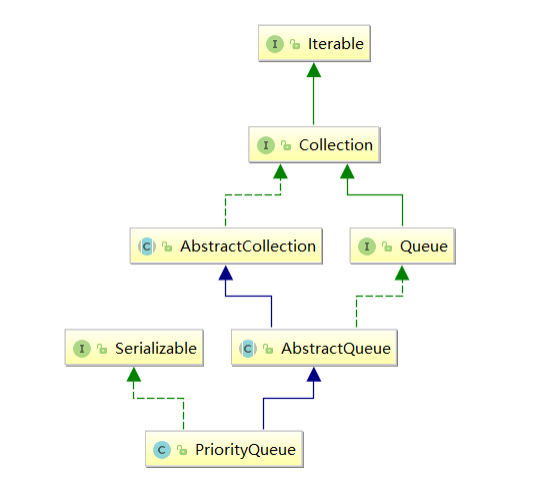
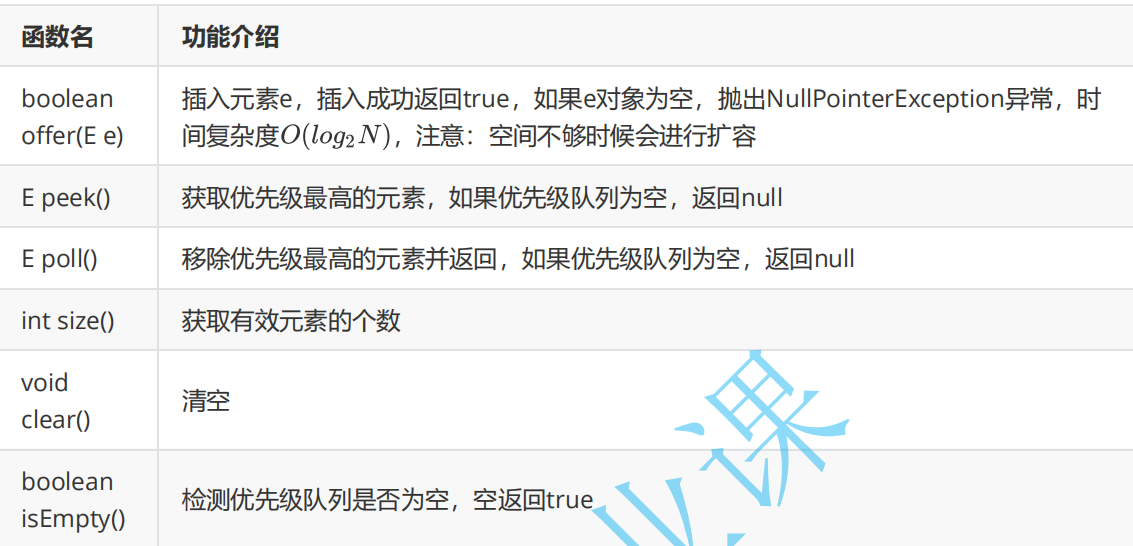
注意事项：
PriorityQueue<Student> priorityQueue1 = new PriorityQueue<>();
priorityQueue1.offer(new Student("zhangsan",10));
priorityQueue1.offer(new Student("lisi",12));1.PriorityQueue放入的元素必须能比较大小，否则会报出下面的错误
2.不能插入null对象，否则会报出下面的错误
PriorityQueue<Student> priorityQueue1 = new PriorityQueue<>();
priorityQueue1.offer(null); 
3.没有容量限制，可以插入任意多个元素，内部会自动扩容
4.插入和删除都是O(logn)
5.使用了最小堆的数据结构，所以每次获取的元素都是最小的元素
oj练习
面试题 17.14. 最小K个数 - 力扣（LeetCode）
设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例：
输入： arr = [1,3,5,7,2,4,6,8], k = 4 输出： [1,2,3,4]
提示：
0 <= len(arr) <= 1000000 <= k <= min(100000, len(arr))
方法一：
建立最小堆，把堆顶k个元素输出出来就行了
代码
public int[] smallestK(int[] arr, int k) {
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
//向上调整 O(logN)
for (int i = 0; i < array.length; i++) {
priorityQueue.offer(array[i]);
}
int[] ret = new int[k];
//k*logN
for (int i = 0; i < k; i++) {
ret[i] = priorityQueue.poll();
}
return ret;
}
虽然通过了，但是时间复杂度有点大
方法二：
1.建立大根堆，大小为k，比如我们可以拿前三个元素来建一个大根堆
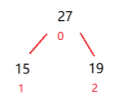
2.从第k+1个元素开始比较，如果比堆顶元素小，则入堆。当前的堆顶元素(较大的)就舍弃掉，因为已经不符合我对前k个最小的元素的要求了
遍历完整个大根堆长这样
问题来了，PriorityQueue是默认采用小根堆的底层，那我们要怎么让它采用大根堆呢
PriorityQueue源码里面的有一个compare函数
这个函数外层是compareTo函数
这两个函数结合一下，把小的放在前面，大的放在后面，所以实现了小根堆的底层
我们可以重写PriorityQueue里面的compare函数，把大的放在前面
class Imp implements Comparator<Integer>{
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
}整个的代码（上面的重写可以扔到匿名内部类里面）
public static int[] smallestK(int[] array, int k) {
int[] ret = new int[k];
if(array == null || k <= 0) {
return ret;
}
//匿名内部类
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
});
//1、建立大小为k的大根堆 O(K*logK)
for (int i = 0; i < k; i++) {
priorityQueue.offer(array[i]);
}
//2、遍历剩下的元素 (N-K)*logK
// (K*logK) + N*logK - K*logK = N*logK -->时间复杂度
for (int i = k; i < array.length; i++) {
int top = priorityQueue.peek();//27
if(array[i] < top) {
priorityQueue.poll();
priorityQueue.offer(array[i]);
}
}
//下面这个不能算topK的复杂度 这个地方是整理数据
//k*logK
for (int i = 0; i < k; i++) {
ret[i] = priorityQueue.poll();
}
return ret;
} 
别看力扣上面的通过时间，我们要自行分析时间复杂度
堆排序
把这个数组从小到大排序，需要建立大根堆
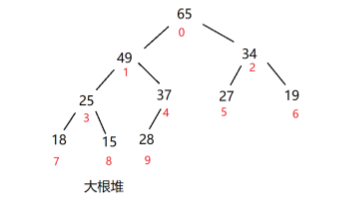
再把这棵树放到堆底，这样最大的元素就有序了
再按照大根堆进行排序（已经有序的元素就不管了），把最大元素49放到堆顶，然后再和堆第的15交换
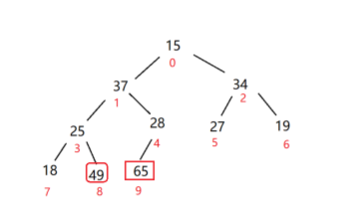
以此类推，设置一个堆底end，每次拿0下标的元素和它交换，交换完end--
public void heapSort(){
int end = usedSize-1;
while(end>0){
swap(0,end);
siftDown(0,end);
end--;
}
}时间复杂度O(N*logN)
![nginx: [emerg] bind() to 0.0.0.0:18888 failed (98: Unknown error）问题解决办法](https://img-blog.csdnimg.cn/b95e361cfb3d4e0cbfcae8a11d0de8c7.png)
