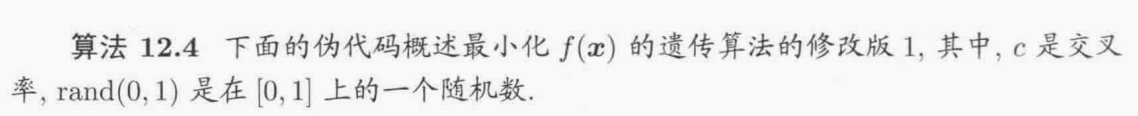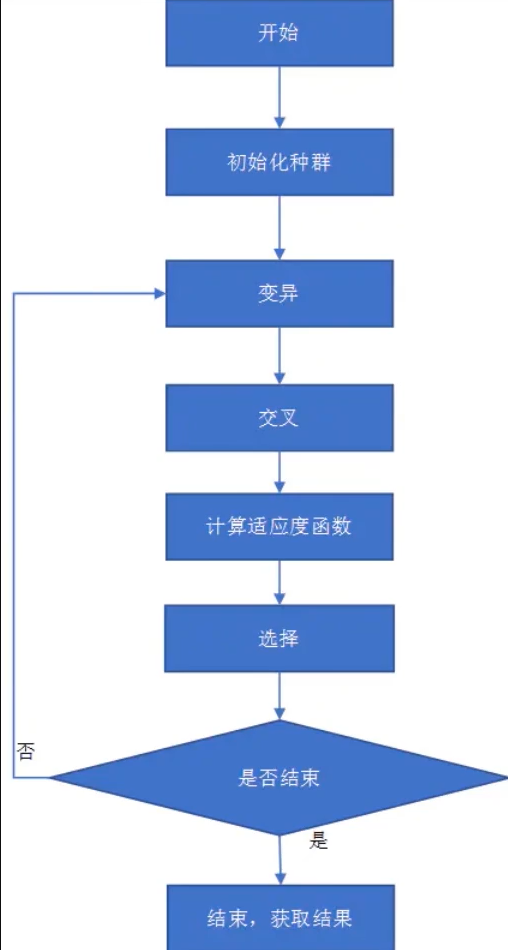
算法流程

12.1 基本差分进化算法

差分进化是为了优化n维连续域中的函数而设计的基于种群的算法。在种群中，每一个个体都是用来表示候选解的一个n维向量。

差分进化算法的基本思路如下：
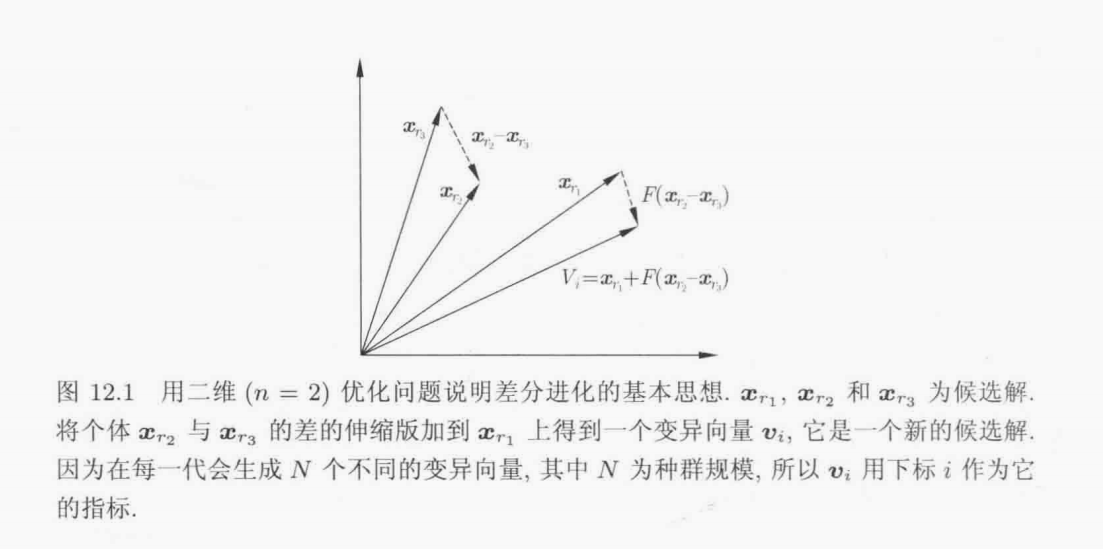
取两个个体之间的差分向量，将这个差分向量的一个伸缩版加到第三个个体上从而产生一个新的候选解，如下图所示：

交叉方式：交叉率c大于r则替换成变异向量v，否则，不变。

参数描述：

在每一对（u，x）中，适应性更强的向量留下来作为差分进化的下一代，扔掉适应性差的向量。


差分进化具体的参数包括步长F，也称为比例因子，以及交叉率c.这些参数依赖于问题，不过通常在F属于[0.4,0.9]和c属于[0.1,1]的范围内挑选。
F的最优值一般随着种群规模N的平方根减小，c的最优值一般随着目标函数的可分离性减小。

我们常称算法12.1为经典差分进化，也称之为DE/rand/1/bin，

12.2 差分进化的变种

12.2.1 试验向量

有许多问题的适应度依赖于解的特征的组合而不是解的单个特征,所以,我们可能需要将解的特征都保留下来,称为DE/rand/1/L,工作方式如下:

例子说明:

算法12.2

12.2.2 变异向量

通过随机决定生成变异向量的方式,可以将不同的方法组合起来.

12.2.3 比例因子的调整

差分进化的比例因子F决定了差分向量对变异向量的影响,到目前为止,我们都假定F是一个常数,随机化是进化算法的标志之一.

可以用两种不同的方式改变差分进化比例因子:
首先,F仍为标量,并在算法12.1中的"for每一个个体"的循环中随机改变,这类变种称颤振.
其次,把F变为n元向量并在“for每一个个体”的循环中随机改变它的每一个元素，于是，变异向量v的每一个元素用差分向量的唯一的缩放分量修改，这类变种被称为抖动。

颤振用下面的语句替换算法12.1中生成变异向量的那一行：

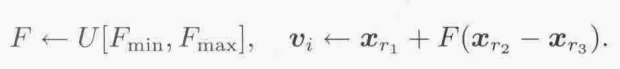
抖动用下面的语句替换算法12.1中生成变异向量的那一行：

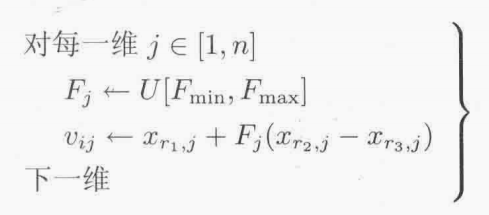
也就是说，在生成变异向量时差分向量的每一个元素会以不同的量伸缩。

一般来说，F的取常值对简单函数似乎很管用，对大多数多峰函数，随机化的F好像很管用。对于大部分可分的函数，抖动最好，对于高度不可分的函数，颤振最好。

12.3 离散优化

在离散域上差分进化只在变异向量时会遇到问题。
回顾算法12.1可知：

12.3.1 混合整数差分进化

显然，要保证v_i∈D的一个方法是将它投影到D上，为了能在离散域上优化，按这种方式修改得到的差分进化方法被称为混合整数差分进化。例如，如果D是n维整数向量的集合，可以用下式替换（12.12）式：

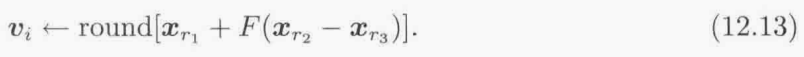
其中round函数对向量按元素操作，其更一般的方式为：

其中P是一个投影算子，对所有x,P(x)∈D. P的一个具体而简单的可能性就是（12.13）式。
一般来说，P会比（12.13）式更复杂，例如，我们仍然假设问题域D是n维整数向量的集合，可以定义P为：

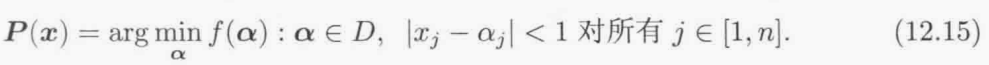
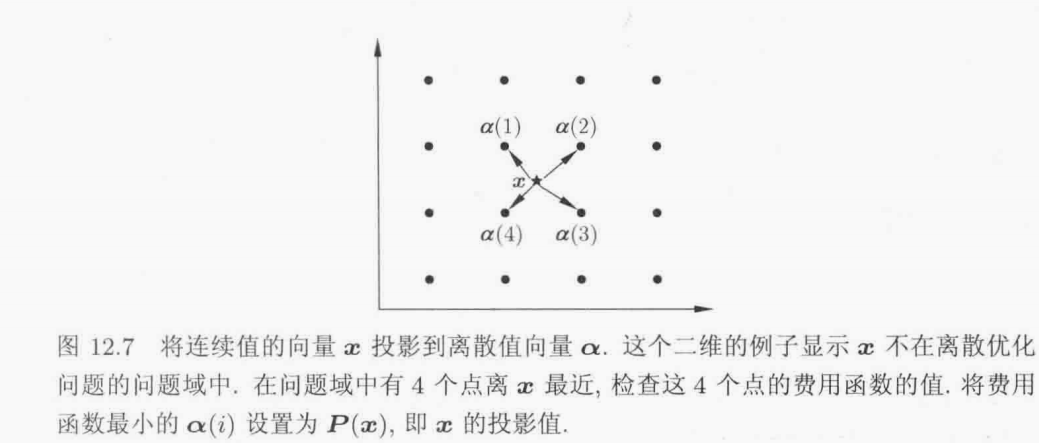
它将取实数值的向量x投影到取整数值的向量α,α 让费用函数最小并且它的每一个元
素与x相应的元素在一个单位之内. 图12.7说明这个想法在二维时的情况.投影算子可能还有别的形式,采用哪一种形式取决于具体的问题.

12.3.2 离散差分进化

为离散问题修改差分进化的另一个方式是改变变异向量的生成方法，直接生成落在离散域D中的变异向量。这种修改方式被称为离散差分进化，利用这个方法，将（12.12）式替换为：

其中，G(·)∈D如果它的所有自变量都在D中，这是（12.14）式的一般化，可见离散差分进化的混合整数差分进化的一般化。我们可以编写函数G(·)，用它来处理一般的离散问题,或者把**G(·)**描述为具体问题的函数.例如,仍然假设D是n维整数向量的集合,则可以用下面的方案生成变异向量:

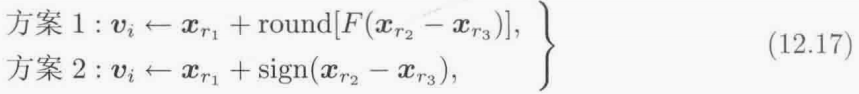
其中，round和sign的函数运算按向量的元素逐个进行。

12.4 差分进化与遗传算法

---