简介
英文名Dijkstra
作用:找到路中指定起点到指定终点的带权最短路径
核心步骤
1)确定起点,终点
2)从未走过的点中选取从起点到权值最小点作为中心点
3)如果满足 起点到中心点权值 + 中心点到指定其他点的权值 < 起点到其他点的权值,
即Weight[start] [center] +Weight [center] [other] < Weight [start] [center] ,
简言之,有更短的路径就取更短的路
理论模拟
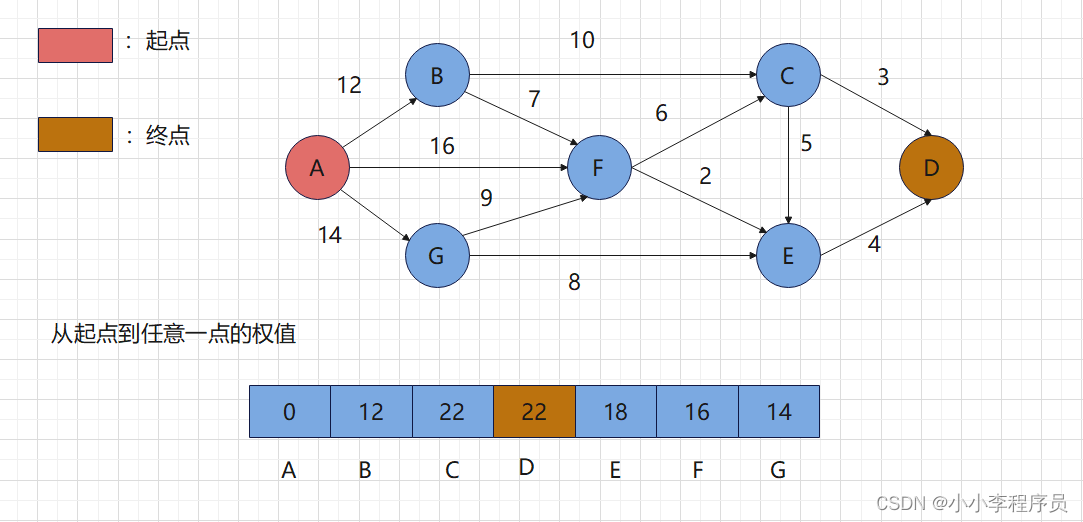
以A为起点,D为终点,如图所示 径, 更新记录更短权值路径

从未走过的点中选取权值最小点,即A作为中心点,标记A走过,更新起点到B、F、G的路径

从未走过的点中选取权值最小点,即B, 并且W:B->C + W:A->C = 12 + 10 < +oo ,更新起点A到C的路径和,
即W: A-> C =W: A-> B -> C =12+10 =22

继续从未走过的点中选取权值最小点G, W: A -> E =+oo > W: A->G ->E =14+8 =22 ,
更新W: A->E 为22

选取F, 由于W:A->F->E=16+2 =18 <22 更新 W: A-> E =18 ,

选取E,由于W:A->E->D=18+4=22<+oo,则更新W: A->D =22

选取C,无可更新点

到达终点D! 最短路径为A->F->E->D ,最短路径和为22
Java代码实现
顶点
//顶点类
public class Vertex {
public String Number; //顶点编号
public List<Vertex>neighborVertexs; //邻居顶点
public Map<Vertex,Integer>weights; //与邻居节点之间的权值
public Vertex(String number) {
this.Number = number;
this.neighborVertexs=new LinkedList<>();
this.weights=new HashMap<>();
}
}边
public class Edge {
public Vertex start;
public Vertex end;
public Integer weight;
public Edge(Vertex start, Vertex end, Integer weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
}最短路径返回结果
public class MinPathResult {
public String minPathString; //将最短路径拼接成字符串形式,如 A->B->C
public List<Vertex>minPathList; //将起点到终点的路径储存在List集合中
public Integer minPathSum; //记录起点到终点的最短路径和
public MinPathResult(List<Vertex> minPathList, String minPathString,Integer minPathSum) {
this.minPathString = minPathString;
this.minPathList = minPathList;
this.minPathSum=minPathSum;
}
@Override
public String toString() {
return "Result{" +
"minPathString:'" + minPathString +" minPathSum:"+minPathSum+
'}';
}
}Dijkstra算法的实现,适用于无向图
import java.util.*;
//适用于无向图
public class DijkstraOperator {
private List<Vertex>vertexs; //全部顶点
private List<Edge>edges; //所有边
private Map<String,Vertex>vertexs_map; //通过顶点编号找到顶点
private final static Integer INF=Integer.MAX_VALUE; //代表无穷大
public DijkstraOperator(List<Vertex> vertexs, List<Edge> edges) {
this.vertexs = vertexs;
this.edges = edges;
this.vertexs_map=new HashMap<>();
//构建编号映射顶点
for(Vertex v:vertexs)
{
vertexs_map.put(v.Number,v);
}
//填充所有顶点的邻居以及权值
for(int i=0;i<edges.size();i++)
{
//填充起点的邻居,以及起点到终点的权值
edges.get(i).start.neighborVertexs.add(edges.get(i).end);
edges.get(i).start.weights.put(edges.get(i).end,edges.get(i).weight);
//填充终点的邻居,以及终点到起点的权值
edges.get(i).end.neighborVertexs.add(edges.get(i).start);
edges.get(i).end.weights.put(edges.get(i).start,edges.get(i).weight);
}
}
//获得从起点到终点之间的路径
public MinPathResult getMinPath(String start, String end){
//用哈希表标记某个顶点是否走过
Map<Vertex,Boolean>visited=new HashMap<>();
//用哈希表记录顶点的前驱
Map<Vertex,Vertex>preVertex=new HashMap<>();
//利用哈希表记录起点到任意一点的最短路径
Map<Vertex,Integer>minPath=new HashMap<>();
//初始化三个表
for(int i=0;i<vertexs.size();i++)
{
//初始化每一个点都未走过
visited.put(vertexs.get(i),false);
//初始化每个点的前驱都是自己
preVertex.put(vertexs.get(i),vertexs.get(i));
//初始化起点到任意两个点之间的最短路径都是无穷大
minPath.put(vertexs.get(i),INF);
}
Vertex startVertex=vertexs_map.get(start);
Vertex endVertex=vertexs_map.get(end);
//填充存在的路径
for(int i=0;i<startVertex.neighborVertexs.size();i++)
{
//设置起点与邻居节点之间的权值
minPath.put(startVertex.neighborVertexs.get(i),startVertex.weights.get(startVertex.neighborVertexs.get(i)));
//设置点前驱
preVertex.put(startVertex.neighborVertexs.get(i),startVertex);
}
//自己到自己的距离为0
minPath.put(startVertex,0);
Vertex curVertex=null;
//一直寻路,直到找到终点
while(curVertex!=endVertex)
{
Integer minWeight=Integer.MAX_VALUE;
curVertex=null;
//能看到的点之间选取距离最小的那个,且这个点并没有走过
for(Vertex v:minPath.keySet())
{
if(!visited.get(v)&&minPath.get(v)<minWeight)
{
//切换中心点
curVertex=v;
//更新最小权值
minWeight=minPath.get(v);
}
}
//如果找不到下一个中心点,说明从起点根本到达不来终点
if(curVertex==null)
return null;
//标记选取点
visited.put(curVertex,true);
//更新权值
for(int i=0;i<curVertex.neighborVertexs.size();i++)
{
//邻居节点
Vertex neighborVertex=curVertex.neighborVertexs.get(i);
//计算起点到邻居节点之间新的权值
int newWeight=minPath.get(curVertex)+curVertex.weights.get(neighborVertex);
//找到能移动的点,如果转折之后距离更短,则记录更短的距离
if(visited.get(neighborVertex)==false&&newWeight<minPath.get(neighborVertex))
{
//记录更短距离
minPath.put(neighborVertex,newWeight);
//记录邻居节点的前驱
preVertex.put(neighborVertex,curVertex);
}
}
}
//起点到终点之间的最短路径
LinkedList<Vertex>targetPath=new LinkedList<>();
for(Vertex curVer=endVertex;curVer!=startVertex;curVer=preVertex.get(curVer))
{
targetPath.addFirst(curVer);
}
targetPath.addFirst(startVertex);
//拼接最短路径
StringBuffer minPathStringBuffer=new StringBuffer();
Integer pathSum=0;
for(int i=0;i< targetPath.size();i++)
{
minPathStringBuffer.append(targetPath.get(i).Number);
if(i!= targetPath.size()-1)
{
pathSum=pathSum+targetPath.get(i).weights.get(targetPath.get(i+1));
minPathStringBuffer.append("->");
}
}
return new MinPathResult(targetPath, minPathStringBuffer.toString(),pathSum);
}
}测试函数
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
List<Vertex>vertexs=new LinkedList<>();
List<Edge>edges=new LinkedList<>();
System.out.println("请输入顶点的数量:");
Integer vexcnt= scanner.nextInt();
System.out.println("请输入这些顶点编号:");
for(int i=0;i<vexcnt;i++)
{
vertexs.add(new Vertex(scanner.next()));
}
System.out.println("请输入边的数量:");
Integer edgecnt= scanner.nextInt();
System.out.println("请输入这些边的端点编号和权值:");
for(int i=0;i<edgecnt;i++)
{
String number1= scanner.next();
String number2= scanner.next();
Integer weight= scanner.nextInt();
Vertex v1=null;
Vertex v2=null;
for(int j=0;j<vertexs.size();j++)
{
if(vertexs.get(j).Number.equals(number1))
v1=vertexs.get(j);
if(vertexs.get(j).Number.equals(number2))
v2=vertexs.get(j);
}
edges.add(new Edge(v1,v2,weight));
}
//定义迪杰斯特拉操作类
DijkstraOperator dijkstra=new DijkstraOperator(vertexs,edges);
//获取任意两点之间的最短路径结果集
List<MinPathResult>minPathResults=new ArrayList<>();
for(int i=0;i< vertexs.size();i++)
{
for(int j=i+1;j< vertexs.size();j++)
{
minPathResults.add(dijkstra.getMinPath(vertexs.get(i).Number,vertexs.get(j).Number));
System.out.println(minPathResults.get(minPathResults.size()-1));
}
}
}
}测试输入与输出结果
//输入部分
请输入顶点的数量:
7
请输入这些顶点编号:
A B C D E F G
请输入边的数量:
12
请输入这些边的端点编号和权值:
A B 12
A F 16
A G 14
B C 10
B F 7
G F 9
G E 8
F C 6
F E 2
C D 3
C E 5
E D 4
//输出部分
Result{minPathString:'A->B minPathSum:12}
Result{minPathString:'A->B->C minPathSum:22}
Result{minPathString:'A->F->E->D minPathSum:22}
Result{minPathString:'A->F->E minPathSum:18}
Result{minPathString:'A->F minPathSum:16}
Result{minPathString:'A->G minPathSum:14}
Result{minPathString:'B->C minPathSum:10}
Result{minPathString:'B->F->E->D minPathSum:13}
Result{minPathString:'B->F->E minPathSum:9}
Result{minPathString:'B->F minPathSum:7}
Result{minPathString:'B->F->G minPathSum:16}
Result{minPathString:'C->D minPathSum:3}
Result{minPathString:'C->E minPathSum:5}
Result{minPathString:'C->F minPathSum:6}
Result{minPathString:'C->E->G minPathSum:13}
Result{minPathString:'D->E minPathSum:4}
Result{minPathString:'D->E->F minPathSum:6}
Result{minPathString:'D->E->G minPathSum:12}
Result{minPathString:'E->F minPathSum:2}
Result{minPathString:'E->G minPathSum:8}
Result{minPathString:'F->G minPathSum:9}
进程已结束,退出代码为 0