2.27每日一题(定积分求面积,旋转体体积)
news2026/2/13 16:17:05
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1148925.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
H5游戏源码分享-像素小鸟游戏(类似深海潜艇)
H5游戏源码分享-像素小鸟游戏(类似深海潜艇) 点击屏幕控制小鸟的飞行高度 整个小游戏就用JS完成
项目地址:https://download.csdn.net/download/Highning0007/88483228
<!DOCTYPE HTML>
<html><head><meta http-equiv…
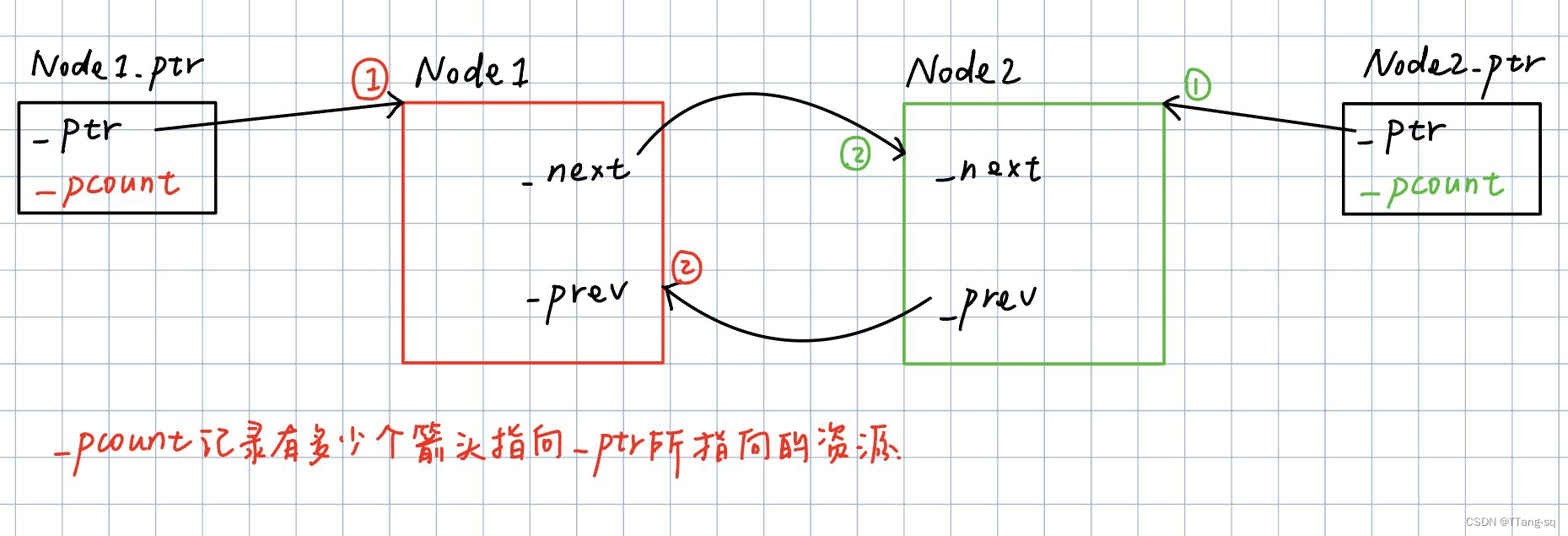
【C++】智能指针总结:auto_ptr、unique_ptr、share_ptr、weak_ptr(技术介绍 + 代码实现)
文章目录 0. 概述智能指针,智能在哪儿?RAII 的介绍四个智能指针的特点: 1. auto_ptr(C98)🐎核心功能的简单实现 2. unique_ptr(C11)🐎核心功能的简单实现 3. shared_ptr&…
【2023MathorCup大数据竞赛】B题完整解答过程(思路+模型文档+代码+结果)
B题完整解答过程 写在最后技术文档(部分)问题分析假设符号说明1 基于自适应ARIMA-LR模型的需求量预测(问题一第一小问)1.1 ARIMA模型的建立1.2 LR模型的建立1.3 自适应混合ARIMA-LR模型的建立1.4 ARIMA模型的求解1.5 LR模型的求解…
图像分类任务ViT与CNN谁更胜一筹?DeepMind用实验证明
精华置顶 墙裂推荐!小白如何1个月系统学习CV核心知识:链接 点击CV计算机视觉,关注更多CV干货
今天跟大家分享DeepMind发表的一篇技术报告,通过实验得出,CNN与ViT的架构之间虽然存在差异,但同等计算资源的预…
力扣刷题 day59:10-29
1.子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
方法一:二进制枚举
#方法一:二进制枚举
def subsets(nums)…
C# “依赖注入” 中的 “三种生命周期”
🚀简介
依赖注入(Dependency Injection,简称DI)是一种实现控制反转(IoC)的技术,用于减少代码之间的耦合度。通过依赖注入,一个类可以从外部获取其依赖的对象,而不是自己…
MyBatis-Plus 与 Druid 结合 Dynamic-datasource 实现多数据源操作数据库
MyBatis-Plus 官网:https://baomidou.com/
MyBatis-Plus 官方文档:https://baomidou.com/pages/24112f/
dynamic-datasource 文档(付费):https://www.kancloud.cn/tracy5546/dynamic-datasource/2264611
创建数据库…
腾讯云2023年双11服务器优惠活动及价格表
腾讯云2023年双11大促活动正在火热进行中,腾讯云推出了一系列服务器优惠活动,云服务器首年1.8折起,买1年送3个月!境外云服务器15元/月起,买更多省更多!下面给大家分享腾讯云双11服务器优惠活动及价格表&…
【论文精读1】MVSNet架构各组织详解
一、训练流程
1. 特征提取
提取N个输入图像的深层特征用作深度匹配
与传统三维重建方法类似,第一步是提取图像特征(SIFT等特征子),不同点在于本文使用8层的卷积网络从图像当中提取更深层的图像特征表示,网络结构如下…
ProEssentials pro v9 历史更新列表--注册版
ProEssentials标准版和专业版之间的唯一区别是可以渲染的数据点和注释的数量。标准版与专业版一样拥有所有的功能和接口。所有版本包括WPF、WinForm、WebForm、ActiveX、VCL和DLL接口。标准版仅限于8000个数据点和800个图表注释。此限制适用于每个控件实例。你可以运行多个控件…
《数字图像处理-OpenCV/Python》连载(33)使用掩模图像控制处理区域
**本书京东优惠购书链接:https://item.jd.com/14098452.html** **本书CSDN独家连载专栏:https://blog.csdn.net/youcans/category_12418787.html** 第 5 章 图像的算术运算 在OpenCV中,图像是以Numpy数组格式存储的,图像的算术运…
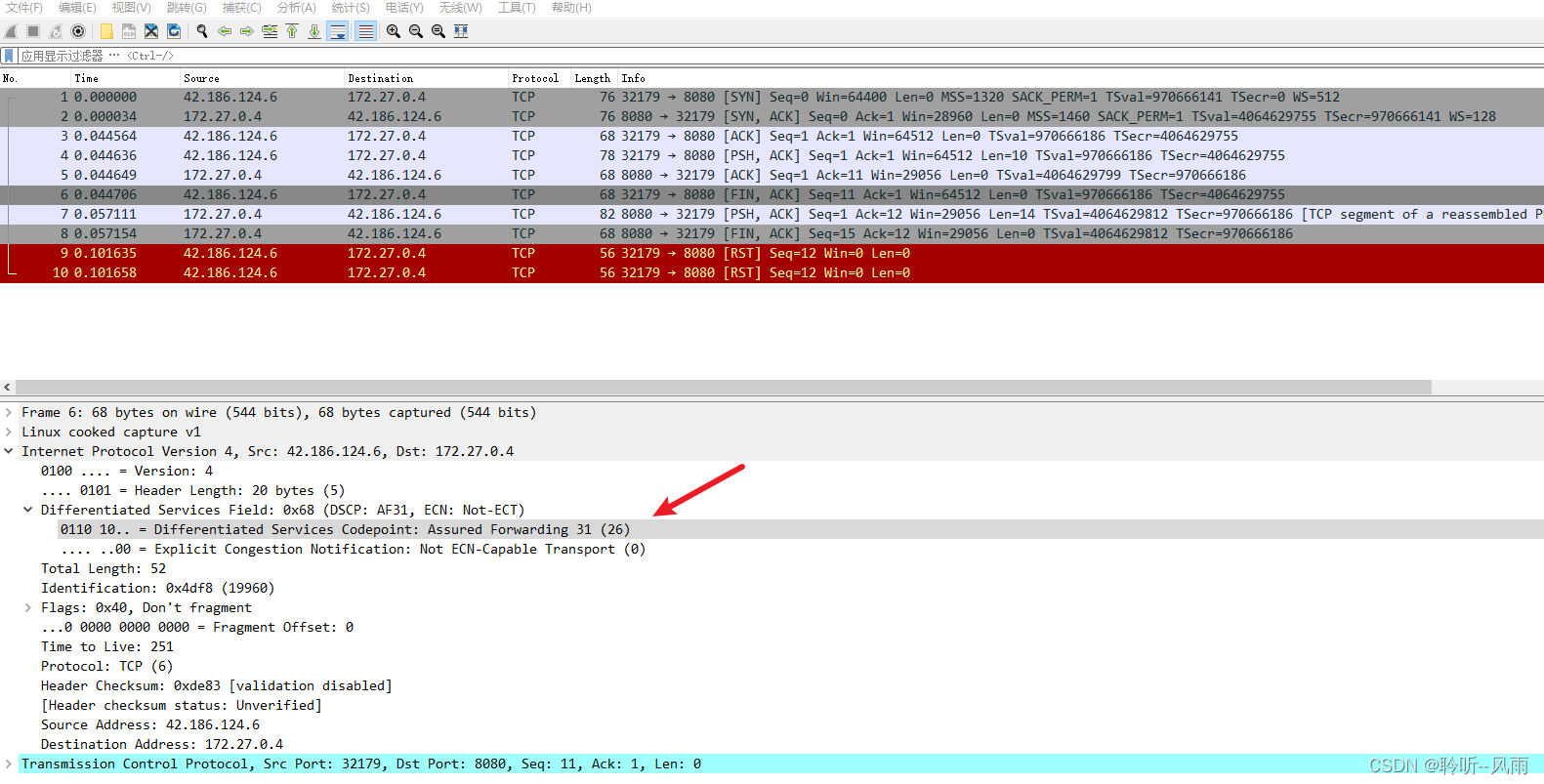
抓包分析DSCP字段在FTP/RSTP协议中的应用
抓包分析DSCP字段在FTP协议中的应用
简介
本文介绍DSCP字段的作用,以及抓包分析DSCP字段在FTP协议中的应用。最后通过实验证明有可能DSCP字段实际上对普通用户没啥用,原因是运营商可能会将用户设置的DSCP字段重置。
DSCP
IP报文中有个TOS字段 &#…
Zynq UltraScale+ XCZU5EV 纯VHDL解码 IMX214 MIPI 视频,2路视频拼接输出,提供vivado工程源码和技术支持
目录 1、前言免责声明 2、我这里已有的 MIPI 编解码方案3、本 MIPI CSI2 模块性能及其优越性4、详细设计方案设计原理框图IMX214 摄像头及其配置D-PHY 模块CSI-2-RX 模块Bayer转RGB模块伽马矫正模块VDMA图像缓存Video Scaler 图像缓存DP 输出 5、vivado工程详解PL端FPGA硬件设计…
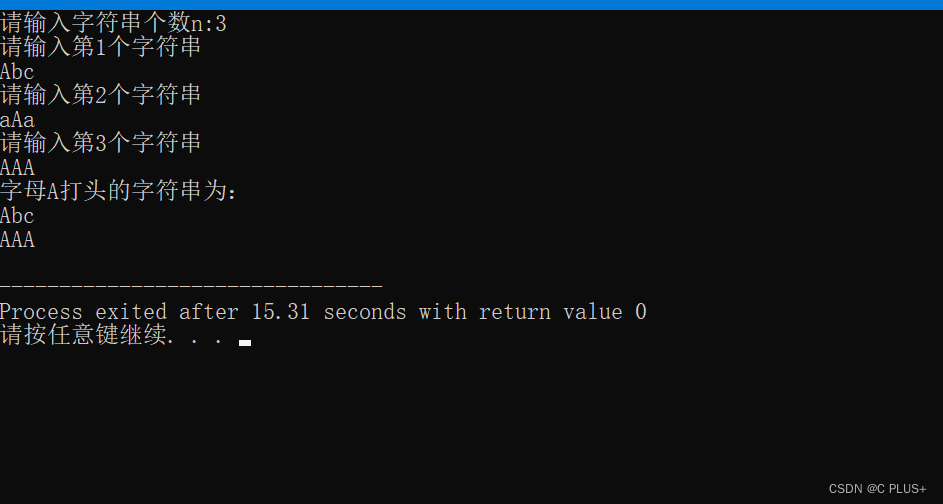
C语言实现输入 n 个字符串,把其中以字母 A 打头的字符串输出
完整代码:
// 输入 n 个字符串,把其中以字母 A 打头的字符串输出。
#include<stdio.h>
#include<stdlib.h>
//字符串的最大长度
#define N 20int main(){int n;printf("请输入字符串个数n:");scanf("%d",&n);//读取…
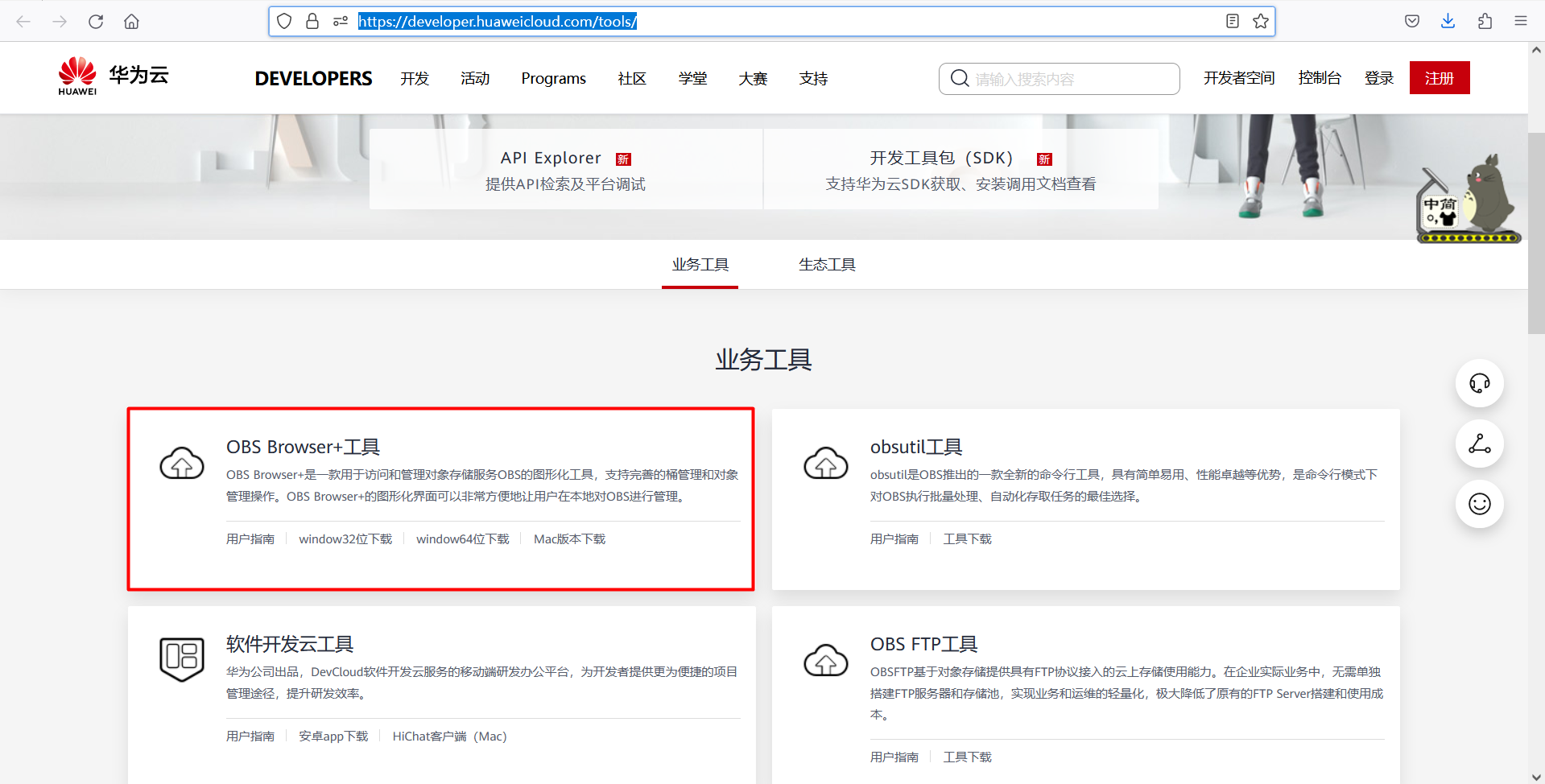
使用OBS Browser+访问华为云OBS存储【Windows】
背景
项目中使用华为云 S3 存储,java 代码中通过华为云 OBS 提供的esdk-obs-java 来访问文件。 但是,通过 JAVA SDK 方式不太方便运维,所以我们需要一款可视化的客户端软件。 华为云 OBS 自身也提供了一款客户端软件,名为 OBS Browser+。
OBS Browser+简介
OBS Browse…
【洛谷算法题】P5709-Apples Prologue / 苹果和虫子【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5709-Apples Prologue / 苹果和虫子【入门2分支结构】🌏题目描述&am…