一、前言

合并排序算法通过采用分治策略和递归思想，实现了高效、稳定的排序功能。本文将深入探讨合并排序算法的原理、实现步骤，并讨论其优缺点。

二、合并排序算法基本原理

合并排序算法采用了分治策略，将一个大问题分解为若干个小问题，并通过递归地解决这些小问题来达到整体解决的目的。具体而言，合并排序首先将待排序的数组不断划分为两个子数组，直到每个子数组只包含一个元素，然后将这些子数组进行两两合并，同时按照大小顺序排列，最终得到完全有序的数组。

三、实现步骤

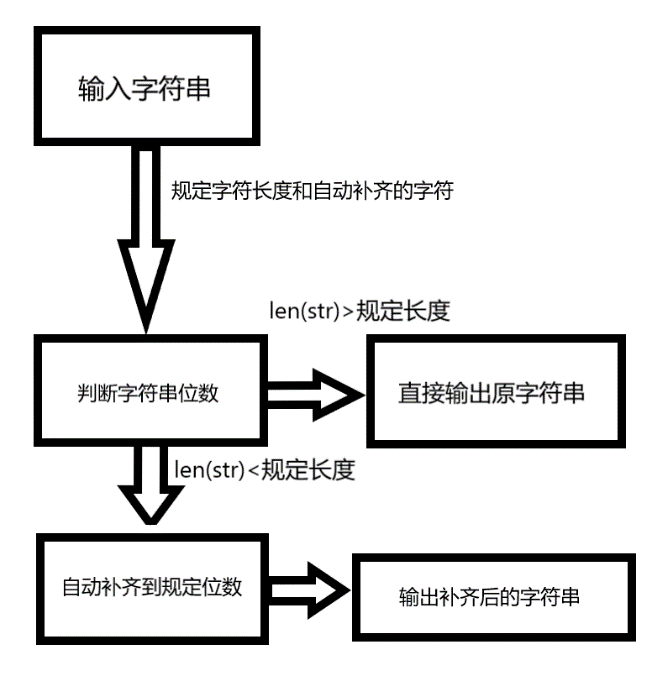
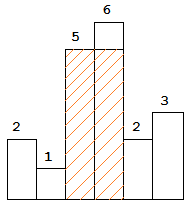
以数组为例，其算法流程原理如图所示。

由图可知，合并排序算法的实现步骤可大致分为三步：

• 第一步-》递归划分：将待排序数组不断划分为两个子数组，直到每个子数组只包含一个元素。
• 第二步-》合并操作：将两个有序的子数组合并为一个有序数组，同时按照大小顺序排列。
• 第三步-》重复上述步骤，直到整个数组排序完成。

以下是使用matlab编写的合并排序算法示例代码：

• 合并排序算法函数

%% 合并排序算法函数
function sorted_array = mergeSort(arr)
    % 检查输入数组是否为空或只有一个元素
    if length(arr) <= 1
        sorted_array = arr;
        return;
    end
    
    % 将输入数组分为两个子数组
    mid = fix(length(arr)/2);
    left_array = arr(1:mid);
    right_array = arr(mid+1:end);
    
    % 递归调用mergeSort函数对子数组进行排序
    left_sorted = mergeSort(left_array);
    right_sorted = mergeSort(right_array);
    
    % 合并两个已排序的子数组
    sorted_array = merge(left_sorted, right_sorted);
end

%% 子数组排序合并函数
function merged_array = merge(arr1, arr2)
    % 初始化指针和合并后的数组
    i = 1; j = 1; k = 1;
    merged_length = length(arr1) + length(arr2);
    merged_array = zeros(1, merged_length);
    
    % 比较两个数组的元素，并按顺序将较小的元素放入合并后的数组中
    while i <= length(arr1) && j <= length(arr2)
        if arr1(i) <= arr2(j)
            merged_array(k) = arr1(i);
            i = i + 1;
        else
            merged_array(k) = arr2(j);
            j = j + 1;
        end
        k = k + 1;
    end
    
    % 将剩余的元素复制到合并后的数组中
    while i <= length(arr1)
        merged_array(k) = arr1(i);
        i = i + 1;
        k = k + 1;
    end
    
    while j <= length(arr2)
        merged_array(k) = arr2(j);
        j = j + 1;
        k = k + 1;
    end
end

• 调用

clc;
clear;
arr = [79,88,70,37,92,6,28,54];
%% 快速排序函数调用
sortedArr= mergeSort(arr);
disp("***********合并排序*****************************");
disp("排序前的数组：");
disp(arr);
disp("排序后的数组：");
disp(sortedArr);

• 结果
  

四、优缺点分析

优点：

• 合并排序算法具有稳定性，相同元素的相对顺序不会改变。
• 在平均情况下，合并排序的时间复杂度为O(nlogn)，较低的时间复杂度保证了其高效性。
• 可以处理大规模数据的排序，适用于各种数据类型。

缺点：

• 合并排序算法需要额外的空间来存储中间结果，空间复杂度为O(n)。
• 对于小规模数据，合并排序的性能可能略低于其他简单的排序算法，由于递归调用的开销。

结论：

合并排序算法通过巧妙地利用分治策略和递归思想，实现了高效、稳定的排序功能。它在实际应用中被广泛使用，并且适用于各种数据类型和规模。然而，在面对特别大的数据集时，需要考虑额外的空间开销。了解合并排序的原理和实现方式，对于深入理解分治策略以及扩展排序算法的知识面都是非常有益的。