一、逻辑回归的理解

前面介绍了线性回归及其衍生回归模型，主要是解决回归问题，即预测的结果是连续的，比如数值。然而有时候，机器学习需要处理样本中的非连续的数据，比如已知某西瓜的质量有“好”和“坏”这两个种类，要对某样本西瓜质量进行预测，这种情况则称为分类问题。

这时就引申出了逻辑回归，逻辑回归(Logistic Regression)是由统计学家大卫·考克斯(David Cox)于1958年提出的。它是一个二元逻辑模型，用于估计一个或多个预测变量(特征)的二元响应概率，用于估计某种事情的可能性。

分类问题要预测的不再是数值，而是两个或者两个以上的类别，即机器学习算法所要完成的是预测输入属于哪个类别。

分类问题的分类 - 二分类(Binary Classification)与多分类(Multi-class Classification)的选择

如果待预测的类别选择只有两个，通常称之为二元分类问题，在机器学习中较多使用 Logistic 函数来解决。
如果待预测的类别选择有两个以上，则称之为多分类问题，在及其学习中较多使用 Softmax 函数来解决。

逻辑回归与线性回归既有非常大的不同：

• 前者为解决分类问题，后者为解决回归问题

也有非常密切的联系：

• 逻辑回归与多元线性回归有很多相同之处，但最大的区别是它们的因变量不同，正因如此，这两种回归同属于一个家族，即广义线性模型(Generalized Linear Model)。

1.1、字面含义

“逻辑回归”由“逻辑”和“回归”两部分组成，它的名字对于初学者来说不太友好。

“逻辑” 为英文单词“Logistic”的音译+简写，或完整叫“逻辑斯蒂”，但还有一种比较高级的叫法为“对数几率”或简称“对数”，即“对数回归”，从数学的角度看，这种叫法最为准确，因为中文“逻辑”与logistic和logit的含义相去甚远。

除此之外，“逻辑”替代了“线性回归”中的“线性”，却完全套用了“线性模型”的思路，即在广义线性模型的基础上衍生而来，这种衍生的模型叫做“逻辑模型”(机器学习中的模型也等同于数学中的函数，还有一种普遍叫法为Logistic函数)。

“回归” - Regression 的含义本来等同于“线性回归”中的“回归”，在加入前面“逻辑”的条件后，就表示为“分类”算法。

1.2、引申

1.2.1、阶跃函数的引入

分类问题的预测结果是离散的，对于二分类问题，我们需要一个函数模型，在变量取任意值的情况下，只会得到两个结果值。在线性回归中，自变量与因变量是一对一或者多对一(一个x对应一个y，或者多个x对应一个y)的情况，显然难以用直线拟合分类问题。

这里引入阶跃函数 - Step Function(或Heaviside Function)，它的图像如下：

阶跃函数是一种特殊的连续时间函数，是一个从0跳变到1的过程，从图中可以看出：
当 $x<0$，$y=0$；当 $x>0$，$y=1$；当 $x=0$，$y$ 为0.5。

阶跃函数在各个领域如自然生态、计算、工程等等拥有非常重要的作用，然而却无法直接用于机器学习：

1. 可导的函数图像是“光滑”的曲线(直线也是特殊的曲线)，而阶跃函数线条非常硬朗，包含两个垂直角位置，明显不可导。
2. 可导的函数一定连续，而实际上，阶跃函数准确图像为两条直线加一个点：当 $x<0$ 时，图像始终为某个值，当 $x>0$ 时，图像又始终为某个值，当 $x=0$ 时，函数的值只能为一个确定的值，阶跃函数包含不连续的点，因此也称为奇异函数，所以图像是不连续的，即不可导。

函数不可导，也就无法运用到机器学习中，去搭配梯度下降等优化算法，使得损失函数的偏差最小。

参考1 单位阶跃函数
参考2 阶跃函数

1.2.2、可导的阶跃函数 - Logistic函数

理解：
原生的阶跃函数不可导，线性函数可导不是阶跃函数不能直接用作分类，如何发明一种函数能满足这两种要求呢？

Logistic函数就正是这种即是可导函数，又是阶跃函数。

Logistic函数使线性模型能够预测离散的分类问题。它由统计学家皮埃尔·弗朗索瓦·韦吕勒于19世纪发明的，它在不同场景中拥有不同的名字：
在逻辑回归算法中，它被称为Logistic函数(曲线)。
在神经网络算法中，它被称为Sigmoid函数。Sigmoid函数即形似S的函数，对率函数是Sigmoid函数最重要的代表。

数学表达式：
$$Logistic(z)=\frac{1}{1+e^{-z}}$$

• $e$ 为自然常数，即一个固定的“常量”。
• $e^{-z}$是以 $e$ 为底、$z$ 为变量的指数函数，也可写成 $exp(-z)$。

函数图像：

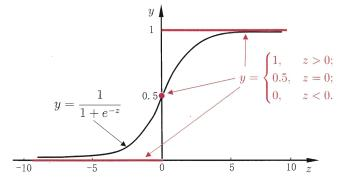
从图中可以看出，该函数将y值转化成一个接近0或1的y值，函数的斜率随着靠近和远离0轴进行放大和缩小，函数“光滑”可导，并且其输出值在y=0附近变化很陡，以0为分界点，$z$ 越小于0，$y$ 越接近于0；$z$ 越大于0，$y$ 越接近于1。

1.2.3、Logistic回归

理解：
Logistic回归即：将线性模型的输出套在Logistic函数内部，于是可以把线性模型的预测结果映射成分类问题所需的预测结果，并且线性模型的输出预测值越小于0或者越大于0越好，即往两极靠效果越好。

表达式：
线性模型：
$$z=w^T{x}_i+b={\beta }^{T}X$$
logistic函数：
$$Logistic(z)=\frac{1}{1+e^{-z}}$$
带入到 logistic函数 中去：
$$H(x)=\frac{1}{1+e^{-(w^T{x}_i+b)}}=\frac{1}{1+e^{-({\beta }^{T}X)}}$$
进行变形：
$$\ln \frac{H(x)}{1-H(x)}=w^{T}x+b$$
若将$H(x)$视为样本$x$作为正例的可能性，则$1-H(x)$是其反例可能性，两者比值：
$$\frac{H(x)}{1-H(x)}$$
称为"几率"(odds)，反映了$x$作为正例的相对可能性。对几率取对数则得到"对数几率"(log odds，亦称logit):
$$\ln \frac{H(x)}{1-H(x)}$$

用线性回归模型的预测结果取逼近真实标记的对数几率，因此对应的模型称为“对数几率回归”(logistic regression，亦称logit regresion)。特别需要注意到，虽然它的名字是“回归”，但实际上却是一种分类学习方法。

这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；它不是仅预测出“类别”，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；此外，对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化计算算法都可以直接用于求取最优解。

$H(x)$表示结果取 $1$ 的概率，于是$1-H(x)$表示结果取 $0$ 的概率，表示为：
$$\ln \frac{p(H(x)=1|x)}{p(H(x)=0|x)}=w^{T}x+b$$
$$P(H(x)=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$
$$P(H(x)=0)=\frac{1}{1+e^{w^{T}x+b}}$$
当函数的结果大于50%时，可以认为属于类别 $1$ 的可能性较高，当然，阈值50%可以结合实际业务进行调整。

1.2.4、回归系数的求解 - 极大似然估计

损失函数：
逻辑回归中损失函数定义为：
$$L(\hat{y},y)=-[y{\log }_2\hat{y}+(1-y){\log }_2(1-\hat{y})]$$
并且 $\hat{y}=H(x)$

• 当真实值 $y=1$ 时，$L(\hat{y},y)=-{\log }_2\hat{y}$。当预测值 $\hat{y}$ 越接近 $1$，$-{\log }_2\hat{y}$ 就越接近值 $0$，表示损失函数值越小，误差越小。当预测值 $\hat{y}$ 越接近 $0$ 时，${\log }_2\hat{y}$ 就越接近负无穷，加上负号后就代表误差越大。
• 当真实值 $y=0$ 时，$L(\hat{y},y)=-{\log }_2(1-\hat{y})$。当预测值 $\hat{y}$ 越接近 $0$，$-{\log }_2\hat{y}$ 就越接近值 $0$，表示损失函数值越小，误差越小。当预测值 $\hat{y}$ 越接近 $1$ 时，${\log }_2\hat{y}$ 就越接近负无穷，加上负号后就代表误差越大。

表达式的由来 - 极大似然估计：
设某次分类事件为 $c$，分类的结果为 Y = { y = 1 , y = 0 } Y=\{y=1, y=0\} Y={y=1,y=0}是互斥事件，于是对于某一次分类事件，符合伯努利分布：
$\begin{array}{rl}P(Y|c)& =P(y=1|c{)}^{y}P(y=0|c{)}^{(1-y)}\\ & =H(x{)}^y(1-H(x){)}^{(1-y)}\\ & ={\hat{y}}^y(1-\hat{y}{)}^{(1-y)}\end{array}$
(由于y为0或1，所以可以表示次数)

为什么加负号？
加上负号：
$\begin{array}{rl}P(Y|c)& =-{\hat{y}}^y(1-\hat{y}{)}^{(1-y)}\end{array}$

逻辑回归采用Logistic函数，结果域为 $(0,1)$，可看做概率模型，即 $x$ 取某个值时 $y$ 为 $1$ 的概率。损失函数采用极大似然估计法，使似然最大，$y$ 为 $1$ 的概率最大，于是加上负号，出现偏差的概率最小。

为什么加 $\log$？
加上 $\log$ 后：
$\log P(Y|c)=-[y{\log }_2\hat{y}+(1-y){\log }_2(1-\hat{y})]$

如果去掉 $\log$，则表示为：
$$L(\hat{y},y)=-[{\hat{y}}^y(1-\hat{y}{)}^{(1-y)}]$$
它不方便运算，为了简化运算，加上 $\log$。

对数函数

对数函数都是单调函数，即要么递增要么递减，一共两类：
底数大于1时，函数单调递增
底数大于0小于1时，函数单调递减

log一般要指明底数，但是各种文献经常出现不带底数的情况，通常有2、10和e三种说法，好在不管哪一种，显然底数都大于1，函数是单调递增的。在Numpy中，log底数默认为e。

二、sklearn的使用

逻辑回归算法在sklearn包中的linear_model模块中，可以参考官网：LogisticRegression

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
X, y = load_iris(return_X_y=True)
clf = LogisticRegression(random_state=0).fit(X, y)
clf.predict(X[:2, :])
# array([0, 0])
clf.predict_proba(X[:2, :])
"""
array([[9.8...e-01, 1.8...e-02, 1.4...e-08],
       [9.7...e-01, 2.8...e-02, ...e-08]])
"""
clf.score(X, y)
# 0.97...

参考

LogisticRegression