文章目录
- A - Ultra-QuickSort
- B - Hanoi Tower Troubles Again! [找规律+递归]
- C - Fibonacci Again[找规律]
- E - [Fire Net](https://programmerall.com/article/7276104269/)[DFS 搜索 ⭐⭐]
- F - Gridland[找规律]
- G - Maximum Subarray Sum[动态规划/分治..经典⭐]
- I - Quoit Design[最近点对距离]
A - Ultra-QuickSort
In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence
9 1 0 5 4 ,
Ultra-QuickSort produces the output
0 1 4 5 9 .
Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.
简单来说,就是有一组无序的数组,求两两交换的最小次数使得数组升序排列。
分析:要使得数组升序排列,
here 🙋 查看归并算法总结
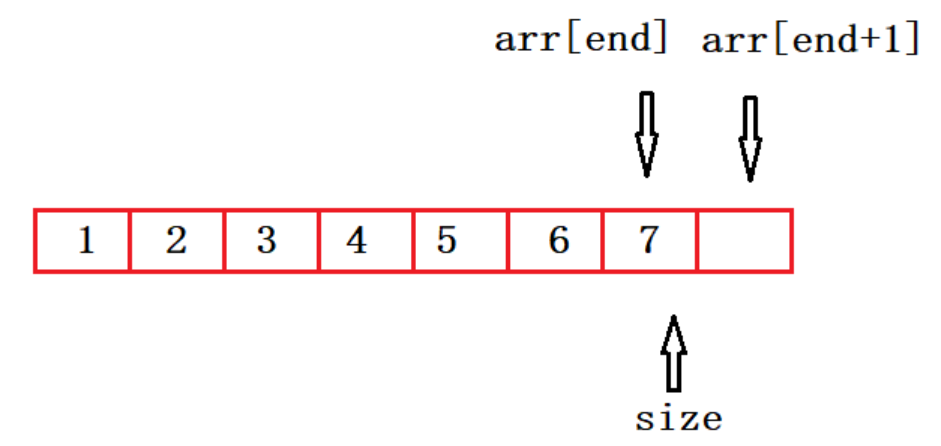
我们只需要在归并排序的算法中,在合并时,判断前面子数列的值是否大于后面子序列的值。
注意一个易错点,每轮loop都必须要指定退出条件,在这里条件就是当两个子序列的指针指向同一个数时,退出。
if(l>=r) return;
整体代码如下,
#include<iostream>
#include<vector>
using namespace std;
int arr[500010];
int tmp[500010];
int sum=0;
//归并算法
void mergesort(int l,int r){
if(l>=r) return;
int mid=(l+r)/2;
mergesort(l,mid);
mergesort(mid+1,r);
int i=l,j=mid+1,k=l;
while(i<=mid && j<=r){
// cout<<"f"; while(arr[i]<=arr[j] && i<=mid) tmp[k++]=arr[i++];
while(arr[i]>arr[j] && j<=r)
{
tmp[k++]=arr[j++];
sum+=mid+1-i;
}
}
while(i<=mid) tmp[k++]=arr[i++];
while(j<=r) tmp[k++]=arr[j++];
for(int k=l;k<=r;k++)
arr[k]=tmp[k];
}
int main(){
int n;
while(cin>>n && n){
for(int i=0;i<n;i++){
cin>>arr[i];
}
sum=0;
mergesort(0,n-1);
cout << sum << endl;
}
}
B - Hanoi Tower Troubles Again! [找规律+递归]
People stopped moving discs from peg to peg after they know the number of steps needed to complete the entire task. But on the other hand, they didn’t not stopped thinking about similar puzzles with the Hanoi Tower. Mr.S invented a little game on it. The game consists of N pegs and a LOT of balls. The balls are numbered 1,2,3… The balls look ordinary, but they are actually magic. If the sum of the numbers on two balls is NOT a square number, they will push each other with a great force when they’re too closed, so they can NEVER be put together touching each other.
The player should place one ball on the top of a peg at a time. He should first try ball 1, then ball 2, then ball 3… If he fails to do so, the game ends. Help the player to place as many balls as possible. You may take a look at the picture above, since it shows us a best result for 4 pegs.
简单来说,看每次提供的柱子数可以承载多少个圆盘,使得每根柱子上相邻两圆盘的加和必定为平方数。
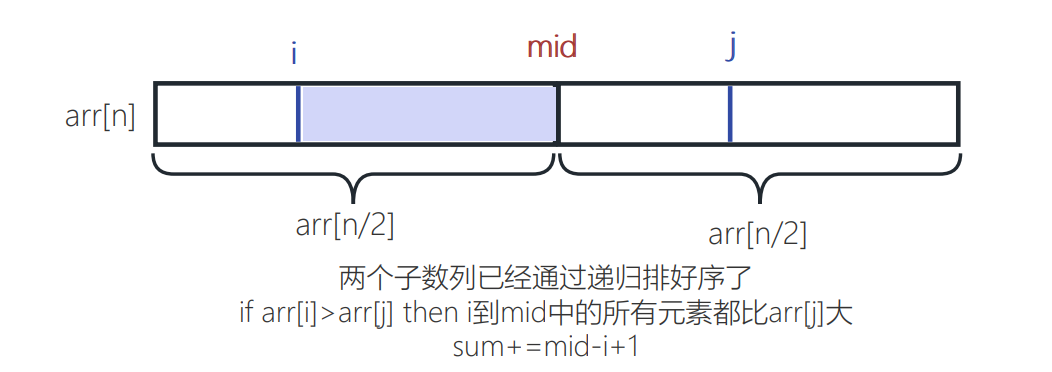
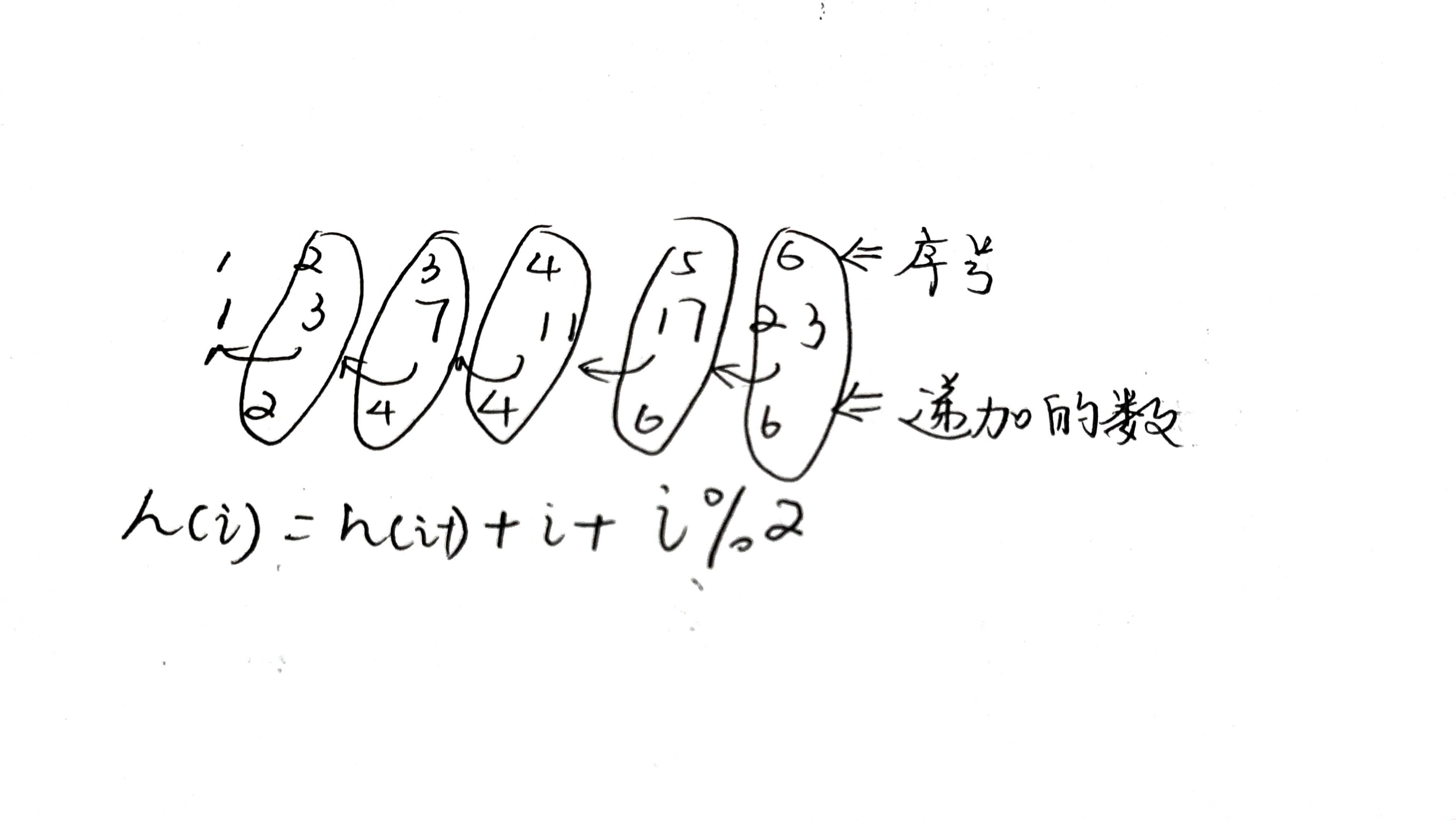
分析:这道题看起来很难,实际上从简单情况入手。先看一根柱子、再看两根柱子…发现能承载圆盘的数量依次为1、3、7、11、17、23,每两个之间相差2、4、4、6、6…于是我们发现了规律。实际上,用数学方法证明也能得出该结论。
递推公式:
H
a
n
o
i
(
i
)
=
H
a
n
o
i
(
i
−
1
)
+
i
+
i
%
2
Hanoi(i)=Hanoi(i-1)+i+i \% 2
Hanoi(i)=Hanoi(i−1)+i+i%2
考虑到题目中有多次求解,所以我们用表格的方式将结果先提前算好存储起来。
void Hanoi(){
table[1]=1;
table[2]=3;
for(int i=3;i<N;i++)
table[i]=table[i-1]+i+i%2;
}
全部代码也就很明晰了:
#include<iostream>
using namespace std;
#define N 55
int table[N];
//打表过程 避免重复计算
void Hanoi(){
table[1]=1;
table[2]=3;
for(int i=3;i<N;i++)
table[i]=table[i-1]+i+i%2;
}
int main(){
int n,x;
cin>>n;
Hanoi();
for(int i=0;i<n;i++){
cin>>x;
cout<<table[x]<<endl;
}
}
补充:
- 宏定义格式
#define 宏名 替换文本
#define N 10; // 宏定义
int c[N]; // 会被替换为: int c[10;];
C - Fibonacci Again[找规律]
There are another kind of Fibonacci numbers: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2)
Input
Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000)
Output
Print the word “yes” if 3 divide evenly into F(n).
Print the word “no” if not.
分析:注意 斐波那契数列会议非常快的速度增长,因此直接计算出结果并和3运算取余的做法不可取。我们考虑列出前面部分结果,试图找规律。嘿,还真成功了!
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 11 | 18 | 29 | 47 | 76 | 123 | 199 | 322 | 521 | 843 |
| √ | √ | √ |
观察表格:发现每4个为一组。在数组的第3个数时,可以被整除,也就是输出yes.
int main(){
int n;
int f[4]={0,0,1,0};
while(cin>>n){
if(f[n%4]) cout<<"yes"<<endl;
else cout<<"no"<<endl;
}
}
E - Fire Net[DFS 搜索 ⭐⭐]
Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.
A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.
Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.
The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.
Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.
分析:
map中各个符号的意义:
| X | . | % |
|---|---|---|
| 有墙(可以避开💣) | 啥也没有 | 有碉堡(可以四处散布💣) |
采用DFS的思想
深度优先搜索的步骤分为
1.递归下去 2.回溯上来。
顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标。这里称之为递归下去。否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路。这便是回溯上来。总结DFS模板:【注意恢复现场这一步】
这道题的IDEA:
从左上角的元素开始进行深度搜索,一直搜索到右下角位置。使用check检查函数判断当前搜索到的位置能不能放置碉堡,若是可以放置,则将本轮的总和加一,并将此处标记为%,意思是有一座碉堡。然后继续进行深度搜索。如果已经到了最右下角位置,则回溯并记录最大值。
#include<iostream>
#include<algorithm>
using namespace std;
int n,ans=0;
char arr[5][5];
int check(int x,int y){
for(int i=x-1;i>=0;i--){
if(arr[i][y]=='%') return false;
if(arr[i][y]=='X') break;
}
for(int i=x+1;i<n;i++){
if(arr[i][y]=='%') return false;
if(arr[i][y]=='X') break;
}
for(int i=y-1;i>=0;i--){
if(arr[x][i]=='%') return false;
if(arr[x][i]=='X') break;
}
for(int i=x+1;i<n;i++){
if(arr[x][i]=='%') return false;
if(arr[x][i]=='X') break;
}
return true;
}
//s表示当前的状态吧
void dfs(int s,int sum){
if(s==n*n){
ans=max(ans,sum);
return;
}
int x=s/n;
int y=s%n;
if(arr[x][y]=='.' && check(x,y)){
arr[x][y]='%'; //表示成功加入一个碉堡
dfs(s+1,sum+1); //继续深度搜索
arr[x][y]='.'; //!还原标记!
}
dfs(s+1,sum);
}
int main(){
while(cin>>n && n){
ans=0;
for(int i=0;i<n;i++)
cin>>arr[i];
dfs(0,0);
cout<<ans<<endl;
}
}
F - Gridland[找规律]
For years, computer scientists have been trying to find efficient solutions to different computing problems. For some of them efficient algorithms are already available, these are the “easy” problems like sorting, evaluating a polynomial or finding the shortest path in a graph. For the “hard” ones only exponential-time algorithms are known. The traveling-salesman problem belongs to this latter group. Given a set of N towns and roads between these towns, the problem is to compute the shortest path allowing a salesman to visit each of the towns once and only once and return to the starting point.
The president of Gridland has hired you to design a program that calculates the length of the shortest traveling-salesman tour for the towns in the country. In Gridland, there is one town at each of the points of a rectangular grid. Roads run from every town in the directions North, Northwest, West, Southwest, South, Southeast, East, and Northeast, provided that there is a neighbouring town in that direction. The distance between neighbouring towns in directions North–South or East–West is 1 unit. The length of the roads is measured by the Euclidean distance. For example, Figure 7 shows 2 × 3-Gridland, i.e., a rectangular grid of dimensions 2 by 3. In 2 × 3-Gridland, the shortest tour has length 6.
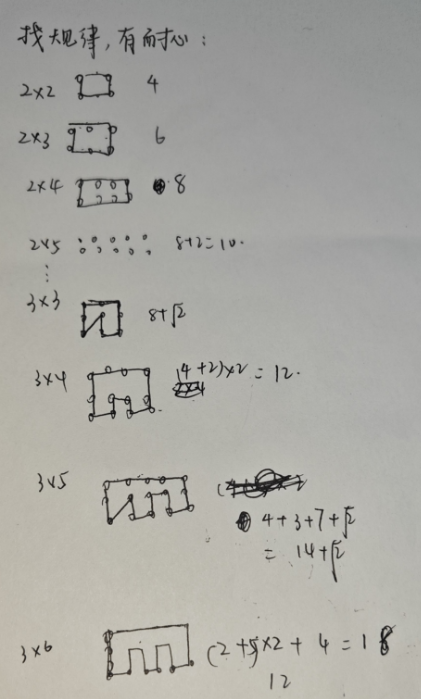
分析:初一看很难,但只要从简单情况出发,找寻规律,就可得到意外之喜😊
只要多做几组你就会发现规律:只要n,m有一个为偶数,答案为n*m;都为基数,答案为n*m-1+sqrt(2)
下图是当时很潦草的草稿…浅浅看一下吧❤
#include<iostream>
#include<math.h>
using namespace std;
int main(){
int N;
double ans;
cin>>N;
for(int i=1;i<=N;i++){
int n,m;
cin>>m>>n;
if((m*n)%2) ans=m*n*1.0-1+sqrt(2);
else ans=m*n*1.0;
cout<<"Scenario #"<<i<<":\n";
printf("%.2f\n\n",ans);
}
}
补充一个知识点:
- prinf输出浮点数
>% - 0 m.n 格式字符
下面对组成格式说明的各项加以说明:
①%:表示格式说明的起始符号,不可缺少。
②-:有-表示左对齐输出,如省略表示右对齐输出。
③0:有0表示指定空位填0,如省略表示指定空位不填。
④m.n:m指域宽,即对应的输出项在输出设备上所占的字符数。N指精度。用于说明输出的实型数的小数位数。为指定n时,隐含的精度为n=6位。
G - Maximum Subarray Sum[动态规划/分治…经典⭐]
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
寻找和最大的子序列,并返回最大值
分析:
刚拿到这道题就想到了用动态规划的方法做。在每一步,我们维护两个变量,一个是全局最优,就是到当前元素为止最优的解是,一个是局部最优,就是必须包含当前元素的最优的解。其中这个局部最优,要么是从这个元素开始的新序列,要么是包含上一个元素的序列。
dp[i]=max(dp[i-1]+arr[i],arr[i]) dp是维护的局部最优解,arr是输入的数组。
#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;
#define N 200100
int main(){
int dp[N];
int arr[N];
int ans=INT_MIN;
//INT_MIN:-2147483648 || INT_MAX:2147483647
int n;
cin>>n;
for(int i=0;i<n;i++)
cin>>arr[i];
dp[0]=arr[0];
for(int i=1;i<n;i++)
{
dp[i]=max(dp[i-1]+arr[i],arr[i]);
ans=max(ans,dp[i]);
}
cout<<ans<<endl;
}
注意这道题目易错点是数组大小的开辟,小心审题就是了。
- 做题时候遇到了:runtime error (运行时错误)就是程序运行到一半,程序就崩溃了。可能有以下几种情况:
①除以零
②数组越界:int a[3]; a[10000000]=10;
③指针越界:int * p; p=(int *)malloc(5 * sizeof(int)); *(p+1000000)=10;
④使用已经释放的空间:int * p; p=(int *)malloc(5 * sizeof(int));free§; *p=10;
⑤数组开得太大,超出了栈的范围,造成栈溢出:int a[100000000];
I - Quoit Design[最近点对距离]
Have you ever played quoit in a playground? Quoit is a game in which flat rings are pitched at some toys, with all the toys encircled awarded.
In the field of Cyberground, the position of each toy is fixed, and the ring is carefully designed so it can only encircle one toy at a time. On the other hand, to make the game look more attractive, the ring is designed to have the largest radius. Given a configuration of the field, you are supposed to find the radius of such a ring.
Assume that all the toys are points on a plane. A point is encircled by the ring if the distance between the point and the center of the ring is strictly less than the radius of the ring. If two toys are placed at the same point, the radius of the ring is considered to be 0.
Input
The input consists of several test cases. For each case, the first line contains an integer N (2 <= N <= 100,000), the total number of toys in the field. Then N lines follow, each contains a pair of (x, y) which are the coordinates of a toy. The input is terminated by N = 0.
Output
For each test case, print in one line the radius of the ring required by the Cyberground manager, accurate up to 2 decimal places.
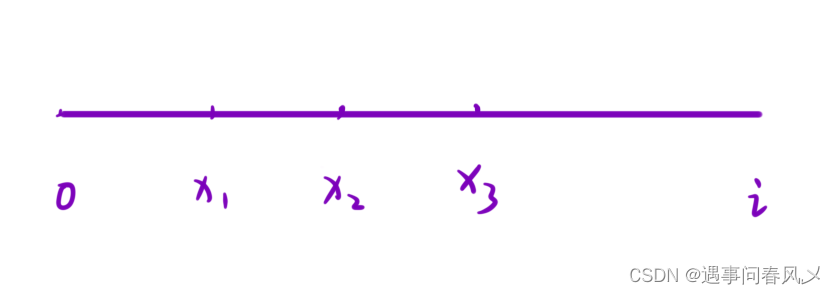
分析:这道题的难点在于读懂题!想要最大的圈直径,使得圈只能套到一个物品。其实就是找最近的两个点,之间的距离就是目标圈的直径。那么就变成了最近点对问题。链接 这个链接展示了详细的求解过程,可以仔细研究。
仔细看





![[C++进阶篇]STL以及string的使用](https://img-blog.csdnimg.cn/a8a361b28b9641b19a0baa6ce246b183.png)

![[读论文] On Joint Learning for Solving Placement and Routing in Chip Design](https://img-blog.csdnimg.cn/a451dee8ac3d446ca6a24f2199df8845.png)