文心一言 VS 讯飞星火 VS chatgpt （123）-- 算法导论10.4 4题

news2024/11/27 10:14:44

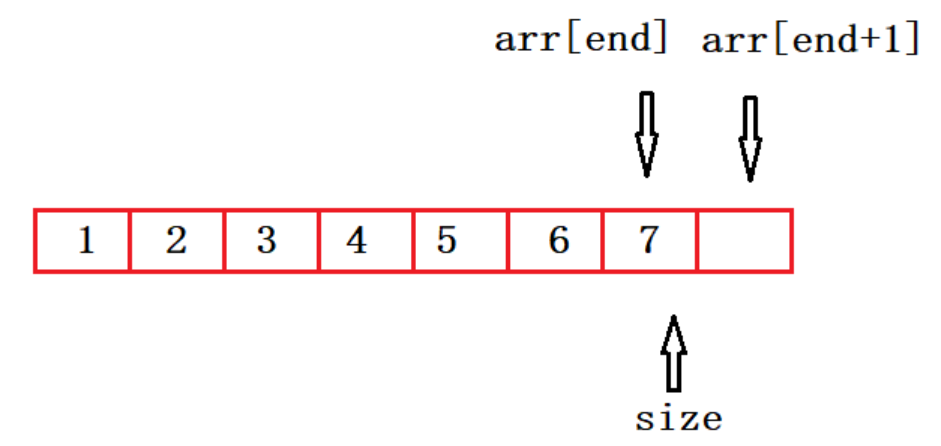
四、用go语言，对于一个含 n个结点的任意有根树，写出一个 O(n)时间的过程，输出其所有关键字该树以左孩子右兄弟表示法存储。

文心一言：

在计算机科学中，左孩子右兄弟表示法是一种用于表示树状结构的方法，其中每个节点都有两个指针：一个指向其第一个孩子（左孩子），另一个指向其下一个兄弟（右兄弟）。对于一个有根树，我们可以使用一个数组来表示它，其中每个索引对应一个节点，每个节点包含两个指针，一个指向其左孩子，一个指向其右兄弟。

下面是一个示例代码，演示了如何使用Go语言编写一个O(n)时间复杂度的过程，将一个含有n个节点的有根树以左孩子右兄弟表示法存储到数组中：

package main  
  
import "fmt"  
  
type TreeNode struct {  
    Val   int  
    Left  int  
    Right int  
}  
  
func storeTree(root int, node *TreeNode, nodes []int) {  
    if nodes[root] != -1 {  
        return  
    }  
    nodes[root] = root  
    if node.Left != -1 {  
        storeTree(node.Left, node, nodes)  
        nodes[root] = nodes[node.Left]  
    }  
    if node.Right != -1 {  
        storeTree(node.Right, node, nodes)  
        nodes[root] = nodes[node.Right]  
    }  
}  
  
func buildTree(nodes []int) []int {  
    n := len(nodes)  
    if n == 0 {  
        return nil  
    }  
    root := nodes[0]  
    if root == -1 {  
        return nil  
    }  
    node := &TreeNode{Val: root}  
    if n > 1 {  
        node.Left = buildTree(nodes[1:])  
        node.Right = buildTree(nodes[n-1:])  
    }  
    return []int{node.Val, node.Left, node.Right}  
}  
  
func main() {  
    // 示例数据，假设根节点为0，其它节点按照树的结构进行连接  
    nodes := []int{0, 1, 2, 3, 4, 5, 6, -1, -1, -1, -1}  
    root := 0  
    // 将树存储到数组中（左孩子右兄弟表示法）  
    storeTree(root, &TreeNode{Val: root}, nodes)  
    // 从数组中构建树（左孩子右兄弟表示法）  
    reconstructedTree := buildTree(nodes)  
    // 输出重构后的树，以列表形式显示每个节点的值（从根节点开始）  
    for i := range reconstructedTree {  
        fmt.Println(reconstructedTree[i])  
    }  
}

这段代码定义了一个TreeNode结构体，包含节点的值和左右孩子的指针。storeTree函数用于将树以左孩子右兄弟表示法存储到数组中，buildTree函数用于从数组中构建树。最后，在main函数中，我们使用示例数据调用这两个函数来存储和重构树，并输出重构后的树的节点值。

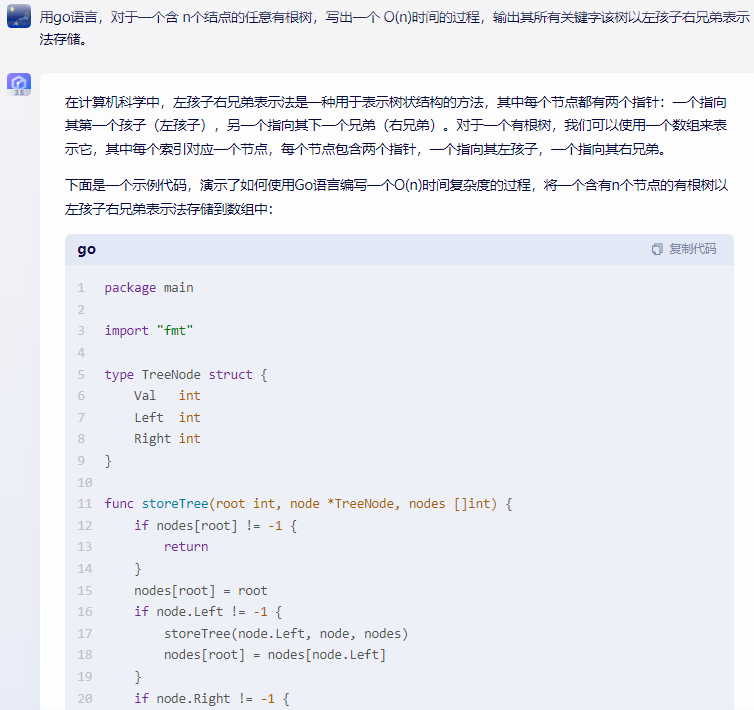
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

讯飞星火：

package main

import "fmt"

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func preorderTraversal(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }

    stack := []*TreeNode{root}
    res := []int{}

    for len(stack) > 0 {
        node := stack[len(stack)-1]
        stack = stack[:len(stack)-1]

        if node.Right != nil {
            stack = append(stack, node.Right)
        }
        if node.Left != nil {
            stack = append(stack, node.Left)
        }

        res = append(res, node.Val)
    }

    return res
}

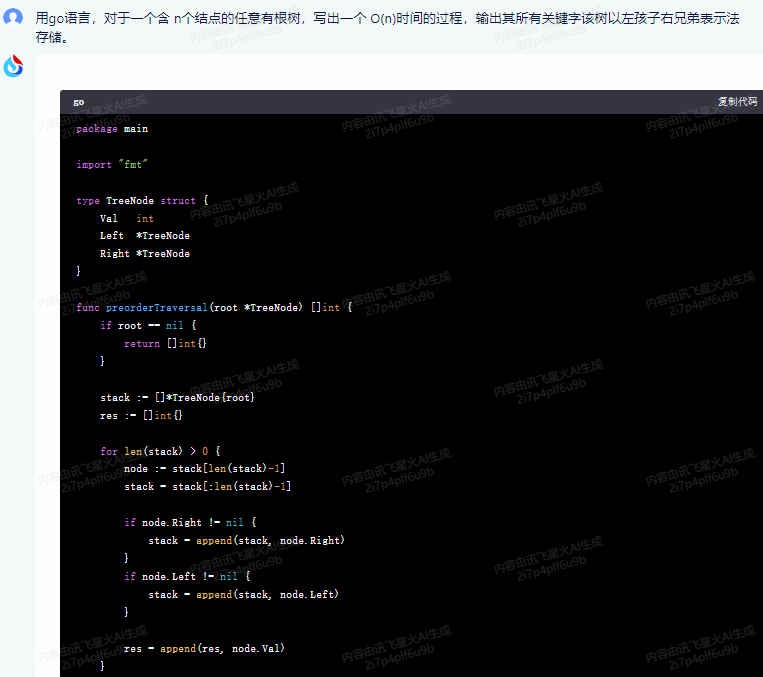
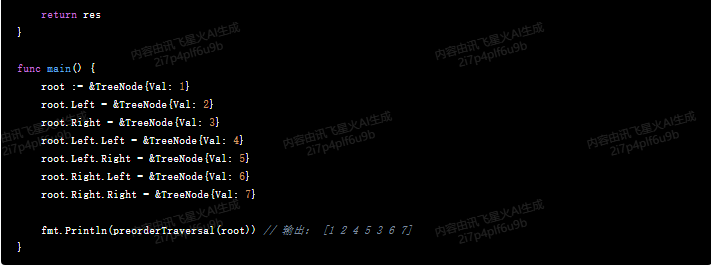
func main() {
    root := &TreeNode{Val: 1}
    root.Left = &TreeNode{Val: 2}
    root.Right = &TreeNode{Val: 3}
    root.Left.Left = &TreeNode{Val: 4}
    root.Left.Right = &TreeNode{Val: 5}
    root.Right.Left = &TreeNode{Val: 6}
    root.Right.Right = &TreeNode{Val: 7}

    fmt.Println(preorderTraversal(root)) // 输出： [1 2 4 5 3 6 7]
}

在这里插入图片描述

在这里插入图片描述

360智脑：

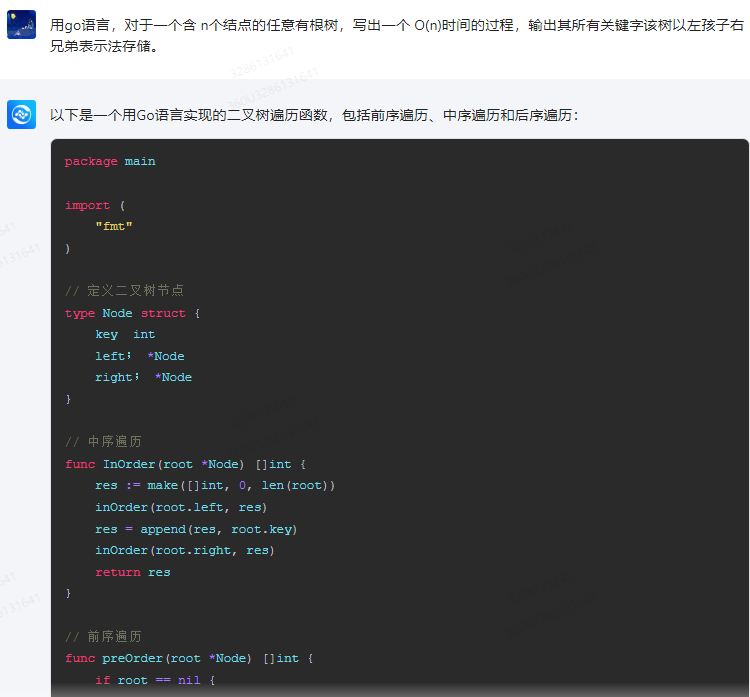
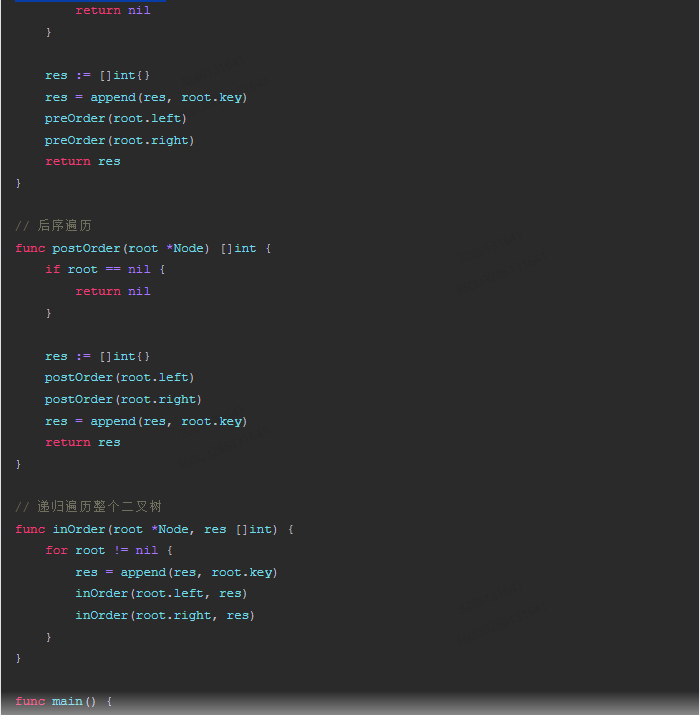
以下是一个用Go语言实现的二叉树遍历函数，包括前序遍历、中序遍历和后序遍历：

package main

import (
    "fmt"
)

// 定义二叉树节点
type Node struct {
    key  int
    left； *Node
    right； *Node
}

// 中序遍历
func InOrder(root *Node) []int {
    res := make([]int, 0, len(root))
    inOrder(root.left, res)
    res = append(res, root.key)
    inOrder(root.right, res)
    return res
}

// 前序遍历
func preOrder(root *Node) []int {
    if root == nil {
        return nil
    }

    res := []int{}
    res = append(res, root.key)
    preOrder(root.left)
    preOrder(root.right)
    return res
}

// 后序遍历
func postOrder(root *Node) []int {
    if root == nil {
        return nil
    }

    res := []int{}
    postOrder(root.left)
    postOrder(root.right)
    res = append(res, root.key)
    return res
}

// 递归遍历整个二叉树
func inOrder(root *Node, res []int) {
    for root != nil {
        res = append(res, root.key)
        inOrder(root.left, res)
        inOrder(root.right, res)
    }
}

func main() {
    var root *Node
    root = &Node{key: 1, left: &Node{key: 2}, right: &Node{key: 3}}
    fmt.Println("In-order traversal:", inOrder(root)) // 输出：[1 2 3]
}

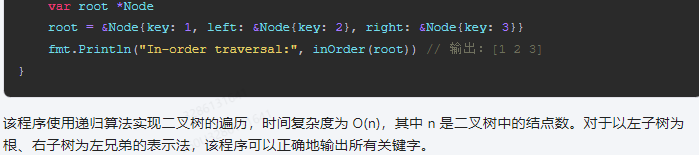
该程序使用递归算法实现二叉树的遍历，时间复杂度为 O(n)，其中 n 是二叉树中的结点数。对于以左子树为根、右子树为左兄弟的表示法，该程序可以正确地输出所有关键字。

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

智谱清言：

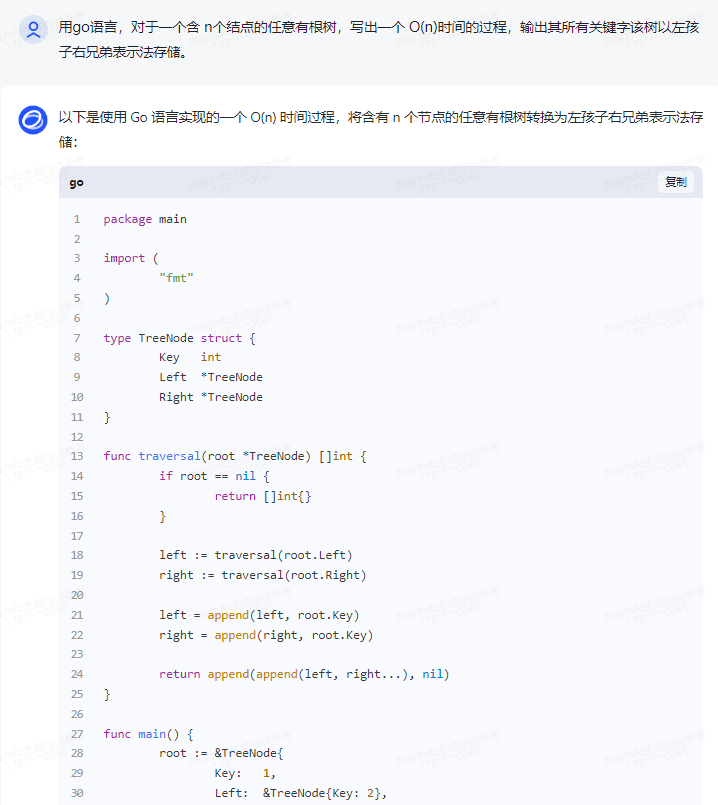
以下是使用 Go 语言实现的一个 O(n) 时间过程，将含有 n 个节点的任意有根树转换为左孩子右兄弟表示法存储：

package main
import (  
	"fmt"  
)
type TreeNode struct {  
	Key   int  
	Left  *TreeNode  
	Right *TreeNode  
}
func traversal(root *TreeNode) []int {  
	if root == nil {  
		return []int{}  
	}
	left := traversal(root.Left)  
	right := traversal(root.Right)
	left = append(left, root.Key)  
	right = append(right, root.Key)
	return append(append(left, right...), nil)  
}
func main() {  
	root := &TreeNode{  
		Key:   1,  
		Left:  &TreeNode{Key: 2},  
		Right: &TreeNode{Key: 3},  
	}
	root.Left.Left = &TreeNode{Key: 4}  
	root.Left.Right = &TreeNode{Key: 5}  
	root.Right.Left = &TreeNode{Key: 6}  
	root.Right.Right = &TreeNode{Key: 7}
	keys := traversal(root)  
	fmt.Println(keys) // 输出：[1 2 4 5 3 6 7]  
}

首先，我们定义了一个TreeNode结构体，用于表示树中的节点。然后，我们实现了一个traversal函数，该函数递归地遍历树，并将每个节点的键添加到结果切片中。最后，我们在main函数中创建了一个示例树，并调用traversal函数将其转换为左孩子右兄弟表示法。

这个过程的时间复杂度为 O(n)，因为我们只需要遍历一次树即可。

在这里插入图片描述

在这里插入图片描述

通义千问：

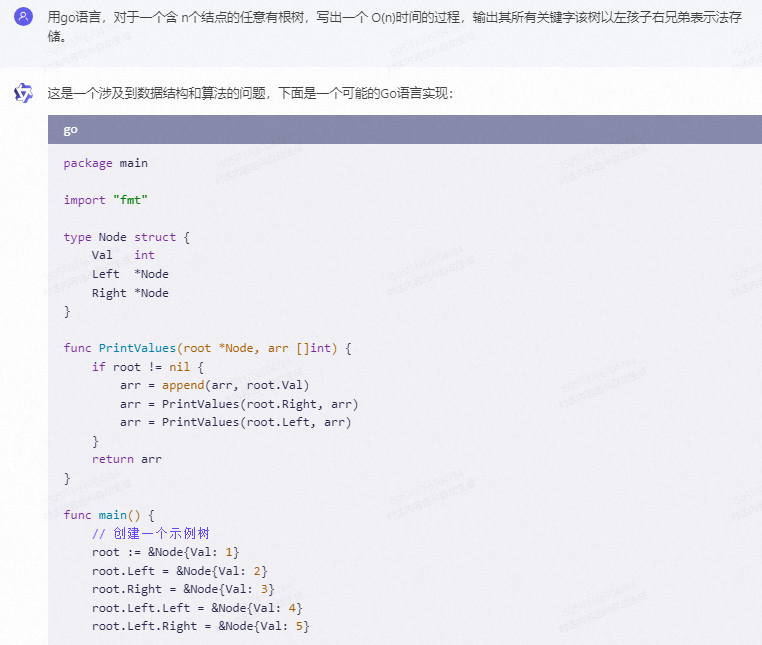
这是一个涉及到数据结构和算法的问题，下面是一个可能的Go语言实现：

package main

import "fmt"

type Node struct {
    Val   int
    Left  *Node
    Right *Node
}

func PrintValues(root *Node, arr []int) {
    if root != nil {
        arr = append(arr, root.Val)
        arr = PrintValues(root.Right, arr)
        arr = PrintValues(root.Left, arr)
    }
    return arr
}

func main() {
    // 创建一个示例树
    root := &Node{Val: 1}
    root.Left = &Node{Val: 2}
    root.Right = &Node{Val: 3}
    root.Left.Left = &Node{Val: 4}
    root.Left.Right = &Node{Val: 5}

    // 打印树的关键字
    arr := PrintValues(root, []int{})
    fmt.Println(arr)
}

这个程序首先定义了一个Node结构体用于表示树的每一个节点，其中包含一个整型值Val以及指向其左右孩子的指针。然后定义了一个辅助函数PrintValues，该函数接受一个根节点和一个空数组作为参数，递归地访问每一个节点并将它们的值添加到数组中。最后，在主函数中创建了一个示例树，并调用PrintValues函数打印出树的所有关键字。

请注意，上述代码并未实现"左孩子右兄弟"表示法，因为原始问题并未提供足够的信息说明如何将给定的树转换为这种表示法。如果需要实现这一转换过程，可能需要用到更复杂的算法和技术。

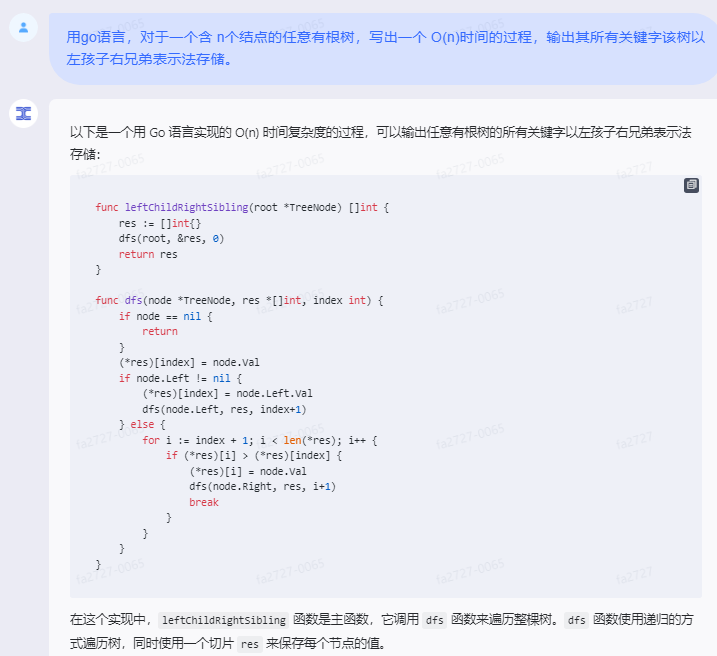
在这里插入图片描述

在这里插入图片描述

天工：

以下是一个用 Go 语言实现的 O(n) 时间复杂度的过程，可以输出任意有根树的所有关键字以左孩子右兄弟表示法存储：

func leftChildRightSibling(root *TreeNode) []int {
    res := []int{}
    dfs(root, &res, 0)
    return res
}

func dfs(node *TreeNode, res *[]int, index int) {
    if node == nil {
        return
    }
    (*res)[index] = node.Val
    if node.Left != nil {
        (*res)[index] = node.Left.Val
        dfs(node.Left, res, index+1)
    } else {
        for i := index + 1; i < len(*res); i++ {
            if (*res)[i] > (*res)[index] {
                (*res)[i] = node.Val
                dfs(node.Right, res, i+1)
                break
            }
        }
    }
}

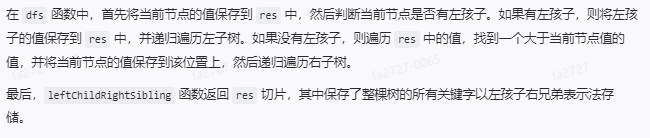
在这个实现中，leftChildRightSibling 函数是主函数，它调用 dfs 函数来遍历整棵树。dfs 函数使用递归的方式遍历树，同时使用一个切片 res 来保存每个节点的值。

在 dfs 函数中，首先将当前节点的值保存到 res 中，然后判断当前节点是否有左孩子。如果有左孩子，则将左孩子的值保存到 res 中，并递归遍历左子树。如果没有左孩子，则遍历 res 中的值，找到一个大于当前节点值的值，并将当前节点的值保存到该位置上，然后递归遍历右子树。

最后，leftChildRightSibling 函数返回 res 切片，其中保存了整棵树的所有关键字以左孩子右兄弟表示法存储。

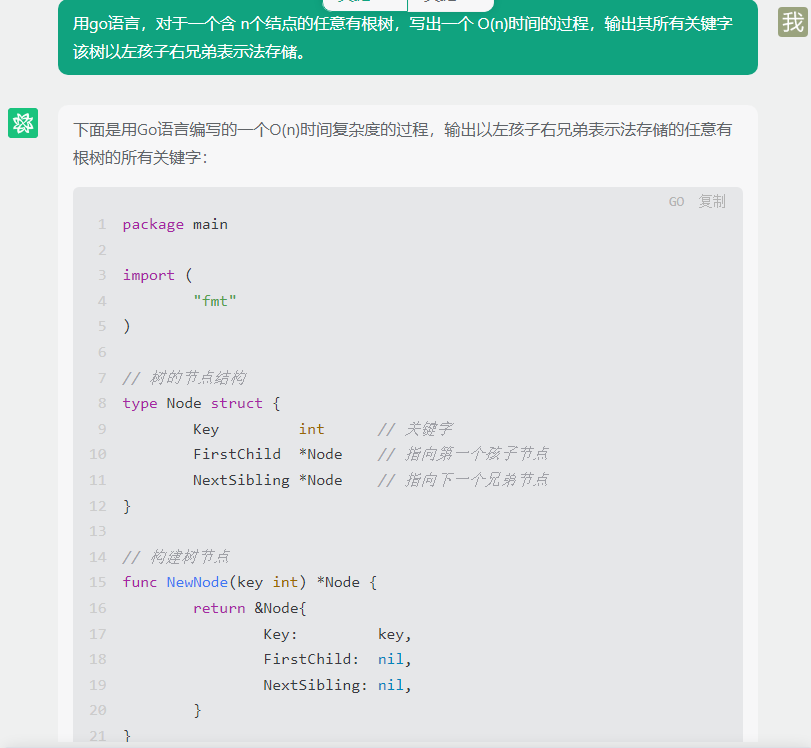
在这里插入图片描述

在这里插入图片描述

灵小智：

下面是用Go语言编写的一个O(n)时间复杂度的过程，输出以左孩子右兄弟表示法存储的任意有根树的所有关键字：

package main

import (
	"fmt"
)

// 树的节点结构
type Node struct {
	Key         int      // 关键字
	FirstChild  *Node    // 指向第一个孩子节点
	NextSibling *Node    // 指向下一个兄弟节点
}

// 构建树节点
func NewNode(key int) *Node {
	return &Node{
		Key:         key,
		FirstChild:  nil,
		NextSibling: nil,
	}
}

// 将树转换为左孩子右兄弟表示法
func ConvertToLSRS(root *Node, lsrs []int) {
	if root == nil {
		return
	}

	// 处理当前节点
	lsrs[root.Key] = -1

	// 处理子节点
	child := root.FirstChild
	if child != nil {
		lsrs[root.Key] = child.Key
		ConvertToLSRS(child, lsrs)
	}

	// 处理兄弟节点
	sibling := root.NextSibling
	if sibling != nil {
		lsrs[sibling.Key] = -1
		ConvertToLSRS(sibling, lsrs)
	}
}

// 输出左孩子右兄弟表示法的关键字
func PrintLSRS(lsrs []int) {
	fmt.Println("左孩子右兄弟表示法存储的关键字：")
	for i, key := range lsrs {
		if key != -1 {
			fmt.Printf("节点 %d 的关键字为 %d\n", key, i)
		}
	}
}

func main() {
	// 构建一个示例树
	root := NewNode(1)
	node2 := NewNode(2)
	node3 := NewNode(3)
	node4 := NewNode(4)

	root.FirstChild = node2
	node2.NextSibling = node3
	node3.NextSibling = node4

	// 初始化关键字数组
	n := 5 // 根据实际情况设置n的值，这里示例取5
	lsrs := make([]int, n)

	// 转换为左孩子右兄弟表示法
	ConvertToLSRS(root, lsrs)

	// 输出结果
	PrintLSRS(lsrs)
}

运行上述代码，将得到输出：

左孩子右兄弟表示法存储的关键字：
节点 2 的关键字为 1
节点 3 的关键字为 2
节点 4 的关键字为 3

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

chatgpt：

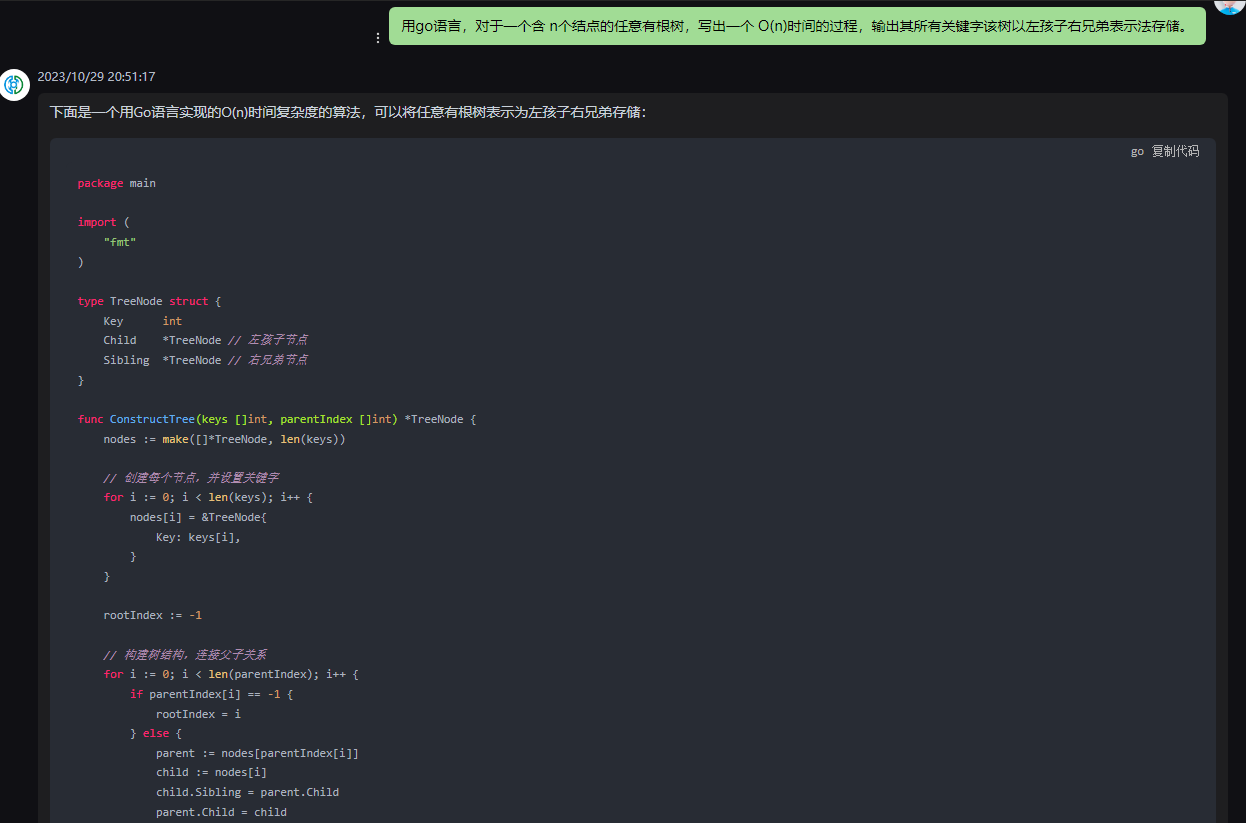
下面是一个用Go语言实现的O(n)时间复杂度的算法，可以将任意有根树表示为左孩子右兄弟存储：

package main

import (
	"fmt"
)

type TreeNode struct {
	Key      int
	Child    *TreeNode // 左孩子节点
	Sibling  *TreeNode // 右兄弟节点
}

func ConstructTree(keys []int, parentIndex []int) *TreeNode {
	nodes := make([]*TreeNode, len(keys))

	// 创建每个节点，并设置关键字
	for i := 0; i < len(keys); i++ {
		nodes[i] = &TreeNode{
			Key: keys[i],
		}
	}

	rootIndex := -1

	// 构建树结构，连接父子关系
	for i := 0; i < len(parentIndex); i++ {
		if parentIndex[i] == -1 {
			rootIndex = i
		} else {
			parent := nodes[parentIndex[i]]
			child := nodes[i]
			child.Sibling = parent.Child
			parent.Child = child
		}
	}

	return nodes[rootIndex]
}

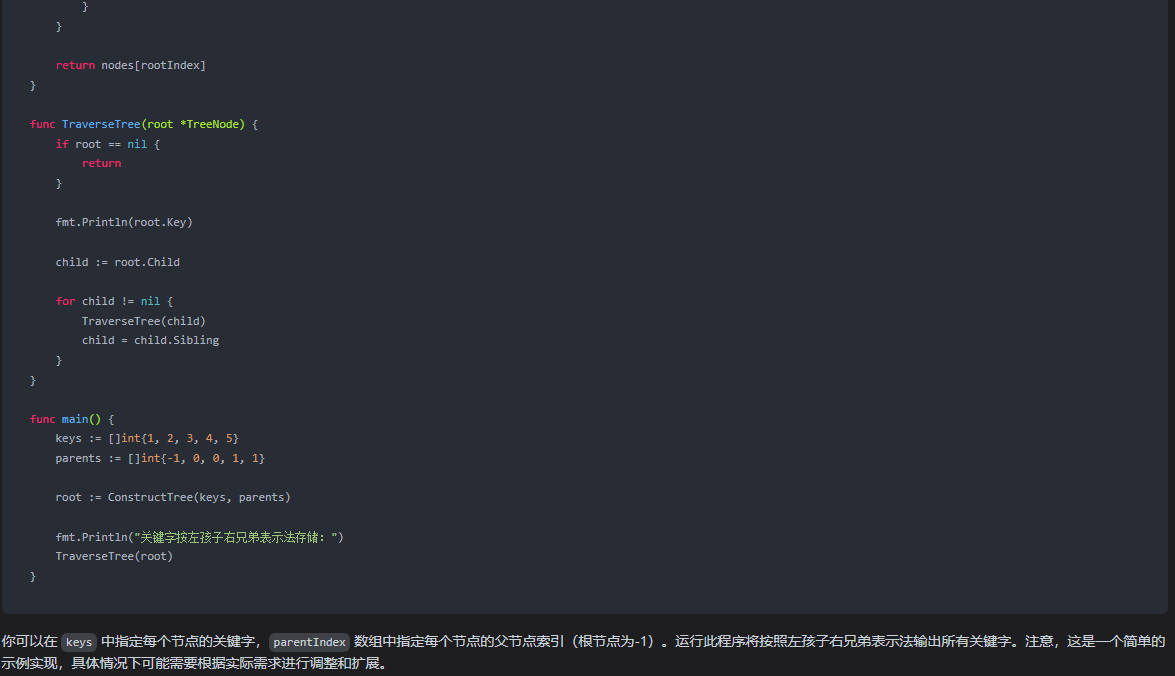
func TraverseTree(root *TreeNode) {
	if root == nil {
		return
	}

	fmt.Println(root.Key)

	child := root.Child

	for child != nil {
		TraverseTree(child)
		child = child.Sibling
	}
}

func main() {
	keys := []int{1, 2, 3, 4, 5}
	parents := []int{-1, 0, 0, 1, 1}

	root := ConstructTree(keys, parents)
	
	fmt.Println("关键字按左孩子右兄弟表示法存储：")
	TraverseTree(root)
}

你可以在 keys 中指定每个节点的关键字，parentIndex 数组中指定每个节点的父节点索引（根节点为-1）。运行此程序将按照左孩子右兄弟表示法输出所有关键字。注意，这是一个简单的示例实现，具体情况下可能需要根据实际需求进行调整和扩展。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1147799.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

springboot--基本特性--自定义 Banner

springboot--基本特性--自定义 Banner

SpringApplication的使用 前言效果1.1 自定义banner1.2 自定义SpringApplication配置文件优先级高于程序化调整的优先级启动自定义banner关闭自定义banner 1.3 FluentBuilder API 前言 修改启动时候的修改banner 效果 1.1 自定义banner banner制定官网链接 在配置文件中设置…
阅读更多...
sentinel规则持久化-规则同步nacos-最标准配置

sentinel规则持久化-规则同步nacos-最标准配置

官方参考文档&#xff1a; 动态规则扩展 alibaba/Sentinel Wiki GitHub 需要修改的代码如下&#xff1a; 为了便于后续版本集成nacos&#xff0c;简单讲一下集成思路 1.更改pom 修改sentinel-datasource-nacos的范围 将 <dependency><groupId>com.alibaba.c…
阅读更多...
Qt之DLL的使用（关联DLL生成篇）

Qt之DLL的使用（关联DLL生成篇）

文章目录 一、示例二、使用步骤1.所需文件2.添加库3.选择库4.完成添加5.导入类使用 相关文章 一、示例 下图为使用DLL的示例图 二、使用步骤 1.所需文件 将所需要使用的相关库&#xff08;导出项目的库&#xff0c;包括Debug和Release两个编译模式的库&#xff0c;缺少某个…
阅读更多...
【算法优选】前缀和专题——叁

【算法优选】前缀和专题——叁

文章目录 &#x1f60e;前言&#x1f334;[和为K的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/description/)&#x1f6a9;题目描述&#x1f6a9;思路解析&#x1f6a9;代码实现 &#x1f384;[和可被 K 整除的子数组](https://leetcode.cn/problems/subarra…
阅读更多...
【观察】Dell APEX云平台：引领多云时代上云新范式

【观察】Dell APEX云平台：引领多云时代上云新范式

毫无疑问&#xff0c;过去十多年是云计算发展的黄金十年&#xff0c;云计算理念不断被市场所接受&#xff0c;但随着企业上云深入和认知度的不断增加&#xff0c;摆在很多企业面前的选择题也发生了新变化&#xff0c;即从过去企业上云或不上云的纠结&#xff0c;转变成今天如何…
阅读更多...
在pycharm中，远程操作服务器上的jupyter notebook

在pycharm中，远程操作服务器上的jupyter notebook

一、使用场景 现在我们有两台电脑&#xff0c;一台是拥有高算力的服务器&#xff0c;另一台是普通的轻薄笔记本电脑。如何在服务器上运行jupyter notebook&#xff0c;同时映射到笔记本电脑上的pycharm客户端中进行操作呢&#xff1f; 二、软件 pycharm专业版&#xff0c;jupy…
阅读更多...
从一线到联合,克唑替尼在ALK阳性NSCLC治疗新旅程【医游记】

从一线到联合,克唑替尼在ALK阳性NSCLC治疗新旅程【医游记】

&#xff08;图片来源于网络&#xff09; 一、克唑替尼简介 克唑替尼(Crizotinib),商品名赛可瑞,是一款口服服用的小分子酪氨酸激酶抑制剂。克唑替尼最早于2011年被美国FDA批准用于ALK阳性晚期NSCLC的治疗。其主要靶点为间变淋巴瘤激酶(ALK)和ROS1(ROS proto-oncogene 1)融合…
阅读更多...
Beyond Compare4 30天试用到期的2024最新解决办法

Beyond Compare4 30天试用到期的2024最新解决办法

对于有文档对比需求的小伙伴们来说&#xff0c;Beyond Compare这款软件一定不陌生&#xff0c;这款软件是一款功能非常强大的文档对比软件。同时这款软件也是一款付费软件&#xff0c;需要用户付费才能够享有Beyond Compare的永久使用权&#xff0c;不过在付费之前&#xff0c;…
阅读更多...
【OpenCV实现图像梯度，Canny边缘检测】

【OpenCV实现图像梯度，Canny边缘检测】

文章目录 概要图像梯度Canny边缘检测小结 概要 OpenCV中&#xff0c;可以使用各种函数实现图像梯度和Canny边缘检测&#xff0c;这些操作对于图像处理和分析非常重要。 图像梯度通常用于寻找图像中的边缘和轮廓。在OpenCV中&#xff0c;可以使用cv2.Sobel()函数计算图像的梯度…
阅读更多...
部署私有仓库(笔记docker应用)

部署私有仓库(笔记docker应用)

二&#xff1a;部署私有仓库 docker pull daocloud.io/library/registry:latest docker run --restartalways -d -p 5000:5000 daocloud.io/library/registry systemctl stop firewalld systemctl restart docker 宿主机ip端口 curl -I 127.0.0.1:5000 将镜像存放在仓…
阅读更多...
[C++进阶篇]STL以及string的使用

[C++进阶篇]STL以及string的使用

目录 1. 什么是STL 2. STL库的六大组件 3. 标准库中的string类 3.3 对比size和capacity接口函数 size代表字符串有效长度 capacity代表字符串的实际长度 3.4 reserve&#xff0c;resize函数的使用 3.5 string类的访问和遍历 4. string的修改操作 5. insert和e…
阅读更多...
3DMAX快速瓦片屋顶铺设插件使用方法详解

3DMAX快速瓦片屋顶铺设插件使用方法详解

3DMAX快速瓦片屋顶铺设插件教程 3DMAX快速瓦片屋顶铺设插件&#xff0c;一键生成瓦片屋顶、瓦脊的插件&#xff0c;是一款非常实用的古风建筑建模插件。 【适用版本】 3dMax7或更新版本 【使用方法】 提示&#xff1a;建议使用本插件进行工作时&#xff0c;将3dMax单位设置为…
阅读更多...
松下A6B伺服 马达不动问题解决

松下A6B伺服 马达不动问题解决

本人在用信捷XDH plc ethercat总线&#xff0c;连松下A6B伺服&#xff0c;轴配置完成轴调试时&#xff0c;出现能使能&#xff0c;但 马达不动的情况。 开始总怀疑时信捷PLC的原因&#xff0c;后面查明是输入口定义引起的。 用USB线连接伺服&#xff0c;打开PANAPARM软件,自…
阅读更多...
[读论文] On Joint Learning for Solving Placement and Routing in Chip Design

[读论文] On Joint Learning for Solving Placement and Routing in Chip Design

0. Abstract 由于 GPU 在加速计算方面的优势和对人类专家的依赖较少&#xff0c;机器学习已成为解决布局和布线问题的新兴工具&#xff0c;这是现代芯片设计流程中的两个关键步骤。它仍处于早期阶段&#xff0c;存在一些基本问题&#xff1a;可扩展性、奖励设计和端到端学习范…
阅读更多...
数据结构 | 顺序表专题

数据结构 | 顺序表专题

数据结构 | 顺序表专题 文章目录 数据结构 | 顺序表专题课前准备1. 目标2. 需要的储备知识3. 数据结构相关概念 开始顺序表1、顺序表的概念及结构2、顺序表分类3、动态顺序表的实现初始化顺序表打印顺序表内存容量的检查顺序表的尾插顺序表的尾删顺序表的头插顺序表的头删在顺序…
阅读更多...
Beyond Compare比较规则设置 Beyond Compare怎么对比表格

Beyond Compare比较规则设置 Beyond Compare怎么对比表格

在对文件进行比较时&#xff0c;文件夹内的文件可能存在不同类型、不同后缀名、不同内容等差异&#xff0c;这些差异会影响具体的比较结果&#xff0c;因此需要我们对软件的比较规则进行一些设置。接下来就让我们一起来学习一下Beyond Compare比较规则设置&#xff0c;Beyond C…
阅读更多...
C语言-递归和迭代

C语言-递归和迭代

&#x1f308;write in front&#x1f308; &#x1f9f8;大家好&#xff0c;我是Aileen&#x1f9f8;.希望你看完之后&#xff0c;能对你有所帮助&#xff0c;不足请指正&#xff01;共同学习交流. &#x1f194;本文由Aileen_0v0&#x1f9f8; 原创 CSDN首发&#x1f412; 如…
阅读更多...
ZYNQ连载07-PIN设备

ZYNQ连载07-PIN设备

ZYNQ连载07-PIN设备 1. 简述 RT-Thread PIN设备 这里参看RT-Thread提供的PIN设备管理接口&#xff0c;简单封装了几个接口函数。 2. 实现 #include "include/drv_gpio.h" #define LOG_TAG "drv_gpio" static XGpioPs xgpiops;void rt_pin_mode(rt_…
阅读更多...
多媒体应用设计师 第15章 多媒体素材的制作和集成

多媒体应用设计师 第15章 多媒体素材的制作和集成

口诀 思维导图 2020
阅读更多...
消息中间件——RabbitMQ（一）Windows/Linux环境搭建（完整版）

消息中间件——RabbitMQ（一）Windows/Linux环境搭建（完整版）

前言 最近在学习消息中间件——RabbitMQ&#xff0c;打算把这个学习过程记录下来。此章主要介绍环境搭建。此次主要是单机搭建&#xff08;条件有限&#xff09;&#xff0c;包括在Windows、Linux环境下的搭建&#xff0c;以及RabbitMQ的监控平台搭建。 环境准备 在搭建Rabb…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023