【算法优选】前缀和专题—

文章目录

😎前言
🌴[和为K的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/description/)
- 🚩题目描述
- 🚩思路解析
- 🚩代码实现
🎄[和可被 K 整除的子数组](https://leetcode.cn/problems/subarray-sums-divisible-by-k/)
- 🚩题目描述
- 🚩解题须知：
- 🚩算法思路：
- 🚩代码实现
🌲[连续数组](https://leetcode.cn/problems/contiguous-array/submissions/)
- 🚩题目描述
- 🚩思路解析
- 🚩代码实现
🍀[矩阵区域和](https://leetcode.cn/problems/matrix-block-sum/)
- 🚩题目描述
- 🚩思路解析
- 🚩代码实现
⭕总结

😎前言

含义：

前缀和实际上就是对于长度为n的数组，我们新建立一个数组长度为n+1，第i个元素的值为前i个元素的和（包括第i个元素）。

特点：

前缀和数组比原数组多一个长度。
前缀和的第0个元素的值为0。
根据前缀和数组的特点，求前缀和时。我们只需要用第i个元素的值+第i-1个前缀个数组的值就可能得到第i个前缀和数组的值。（这也是一种动态规划的思想）。

应用：

前缀和算法可以解决一些在数组中与连续有关的问题

🌴和为K的子数组

🚩题目描述

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。

子数组是数组中元素的连续非空序列。

示例 1：
输入：nums = [1,1,1], k = 2
输出：2
示例 2：
输入：nums = [1,2,3], k = 3
输出：2

class Solution {
    public int subarraySum(int[] nums, int k) {

    }
}

🚩思路解析

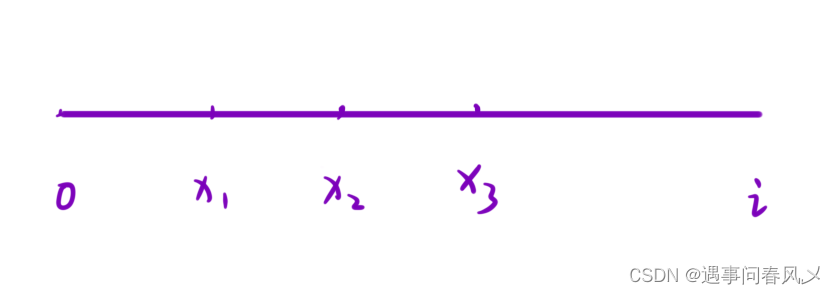
在这里插入图片描述
设 i 为数组中的任意位置，⽤ sum[i] 表⽰ [0, i] 区间内所有元素的和。

想知道有多少个「以 i 为结尾的和为 k 的⼦数组」，就要找到有多少个起始位置为 x1, x2,x3… 使得 [x, i] 区间内的所有元素的和为 k 。

那么 [0, x] 区间内的和是不是就是sum[i] - k 了。于是问题就变成：

找到在 [0, i - 1] 区间内，有多少前缀和等于 sum[i] - k 的即可。

我们不⽤真的初始化⼀个前缀和数组，因为我们只关⼼在 i 位置之前，有多少个前缀和等于sum[i] - k 。因此，我们仅需⽤⼀个哈希表，⼀边求当前位置的前缀和，⼀边存下之前每⼀种前缀和出现的次数

🚩代码实现

class Solution {
    public int subarraySum(int[] nums, int k) {
        Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
        hash.put(0, 1);
        int sum = 0;
        int ret = 0;
        for(int x : nums)
        {
            sum += x; // 计算当前位置的前缀和
            ret += hash.getOrDefault(sum - k, 0); // 统计结果
            hash.put(sum, hash.getOrDefault(sum, 0) + 1); // 把当前的前缀和丢到哈希表⾥⾯
        }
        return ret;
    }
}

🎄和可被 K 整除的子数组

🚩题目描述

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的（连续、非空）子数组的数目。

子数组是数组的连续部分。

示例 1：
输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
输入: nums = [5], k = 9
输出: 0

class Solution {
    public int subarraysDivByK(int[] nums, int k) {

    }
}

🚩解题须知：

同余定理

如果 (a - b) % n == 0 ，那么我们可以得到⼀个结论： a % n = = b % n 。

⽤⽂字叙述就是，如果两个数相减的差能被n整除，那么这两个数对n取模的结果相同。

Java中负数取模的结果，以及如何修正「负数取模」的结果

Java中关于负数的取模运算，结果是「把负数当成正数，取模之后的结果加上⼀个负号」。

例如： -1 % 3 = -(1 % 3) = -1

因为有负数，为了防⽌发⽣「出现负数」的结果，以 (a % n + n) % n 的形式输出保证为正。

例如： -1 % 3 = (-1 % 3 + 3) % 3 = 2

🚩算法思路：

思路与和为K的⼦数组这道题的思路相似
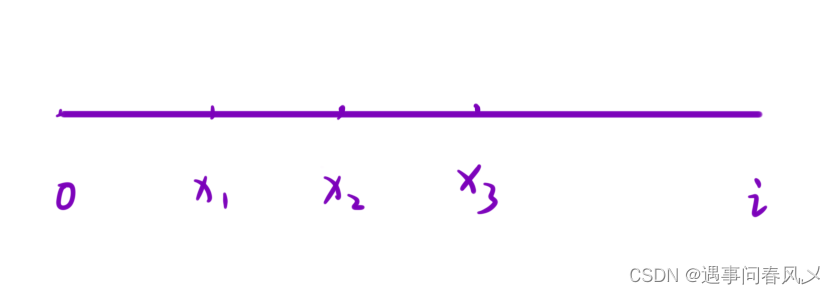
在这里插入图片描述
设 i 为数组中的任意位置，⽤ sum[i] 表⽰ [0, i] 区间内所有元素的和。

想知道有多少个「以 i 为结尾的可被 k 整除的⼦数组」，就要找到有多少个起始位置为 x1,x2, x3… 使得 [x, i] 区间内的所有元素的和可被 k 整除。
设 [0, x - 1] 区间内所有元素之和等于 a ， [0, i] 区间内所有元素的和等于 b ，可得(b - a) % k == 0 。
由同余定理可得， [0, x - 1] 区间与 [0, i] 区间内的前缀和同余。于是问题就变成：
- 找到在 [0, i - 1] 区间内，有多少前缀和的余数等于 sum[i] % k 的即可。

我们不⽤真的初始化⼀个前缀和数组，因为我们只关⼼在 i 位置之前，有多少个前缀和等于sum[i] - k 。因此，我们仅需⽤⼀个哈希表，⼀边求当前位置的前缀和，⼀边存下之前每⼀种前缀和出现的次数。

🚩代码实现

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        Map<Integer, Integer> hash = new HashMap<Integer, Integer>();
        hash.put(0 % k, 1);
        int sum = 0;
        int ret = 0;
        for(int x : nums)
        {
            sum += x; // 计算当前位置的前缀和
            int r = (sum % k + k) % k;
            ret += hash.getOrDefault(r, 0); // 统计结果
            hash.put(r, hash.getOrDefault(r, 0) + 1);
        }
        return ret;
    }
}

🌲连续数组

🚩题目描述

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

示例 1:
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

class Solution {
    public int findMaxLength(int[] nums) {

    }
}

🚩思路解析

稍微转化⼀下题⽬，就会变成我们熟悉的题：

本题让我们找出⼀段连续的区间， 0 和 1 出现的次数相同。
如果将 0 记为 -1 ， 1 记为 1 ，问题就变成了找出⼀段区间，这段区间的和等于 0 。
于是，就和560.和为K的⼦数组这道题的思路⼀样

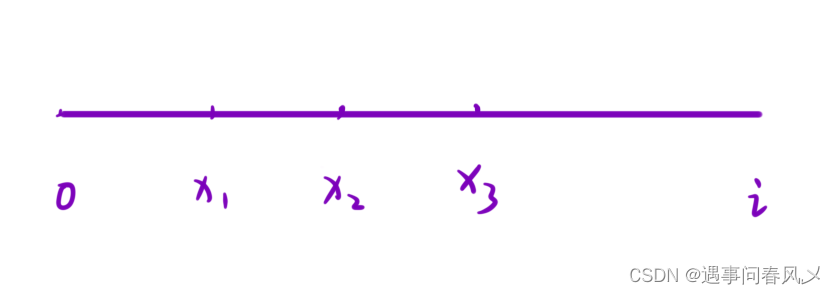
在这里插入图片描述
设 i 为数组中的任意位置，⽤ sum[i] 表⽰ [0, i] 区间内所有元素的和。
想知道最⼤的「以 i 为结尾的和为 0 的⼦数组」，就要找到从左往右第⼀个 x1 使得 [x1, i] 区间内的所有元素的和为 0 。那么 [0, x1 - 1] 区间内的和是不是就是 sum[i] 了。于是问题就变成：

找到在 [0, i - 1] 区间内，第⼀次出现 sum[i] 的位置即可。我们不⽤真的初始化⼀个前缀和数组，因为我们只关⼼在 i 位置之前，第⼀个前缀和等于 sum[i] 的位置。因此，我们仅需⽤⼀个哈希表，⼀边求当前位置的前缀和，⼀边记录第⼀次出现该前缀和的位置。

🚩代码实现

class Solution {
    public int findMaxLength(int[] nums) {
        Map<Integer,Integer> hashmap = new HashMap<>();
        hashmap.put(0,-1);
        int sum = 0;
        int ret = 0;
        for(int i = 0; i < nums.length; i++) {
            sum += (nums[i] == 0 ? -1 : 1);
            if(hashmap.containsKey(sum)) {
                ret = Math.max(ret,i - hashmap.get(sum));
            } else {
                hashmap.put(sum,i);
            }
        }
        return ret;
    }
}

🍀矩阵区域和

🚩题目描述

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：

i - k <= r <= i + k, j - k <= c <= j + k 且(r, c) 在矩阵内。

示例 1：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]
示例 2：
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

class Solution {
    public int[][] matrixBlockSum(int[][] mat, int k) {

    }
}

🚩思路解析

⼆维前缀和的简单应⽤题，关键就是我们在填写结果矩阵的时候，要找到原矩阵对应区域的「左上⻆」以及「右下⻆」的坐标（推荐⼤家画图）

关于二维前缀和的求法，不懂得宝子可以去看看博主写的《【算法优选】前缀和专题——壹》进行查看学习

左上⻆坐标： x1 = i - k，y1 = j - k ，但是由于会「超过矩阵」的范围，因此需要对 0 取⼀个 max 。因此修正后的坐标为： x1 = max(0, i - k), y1 = max(0, j - k) ;
右下⻆坐标： x1 = i + k，y1 = j + k ，但是由于会「超过矩阵」的范围，因此需要对 m- 1 ，以及 n - 1 取⼀个 min 。因此修正后的坐标为： x2 = min(m - 1, i + k),
y2 = min(n - 1, j + k)

然后将求出来的坐标代⼊到「⼆维前缀和矩阵」的计算公式上即可~（但是要注意下标的映射关系）

🚩代码实现

class Solution {
    public int[][] matrixBlockSum(int[][] mat, int k) {
        int m = mat.length, n = mat[0].length;
        // 1. 预处理前缀和矩阵
        int[][] dp = new int[m + 1][n + 1];
        for(int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        // 2. 使⽤
        int[][] ret = new int[m][n];
        for(int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int x1 = Math.max(0, i - k) + 1;
                int y1 = Math.max(0, j - k) + 1;
                int x2 = Math.min(m - 1, i + k) + 1;
                int y2 = Math.min(n - 1, j + k) + 1;
                ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
            }
        }
        return ret;
    }
}