拓扑排序
如果说最短路径是有环图的应用,那么拓扑排序就是无环图的应用。
拓扑排序介绍
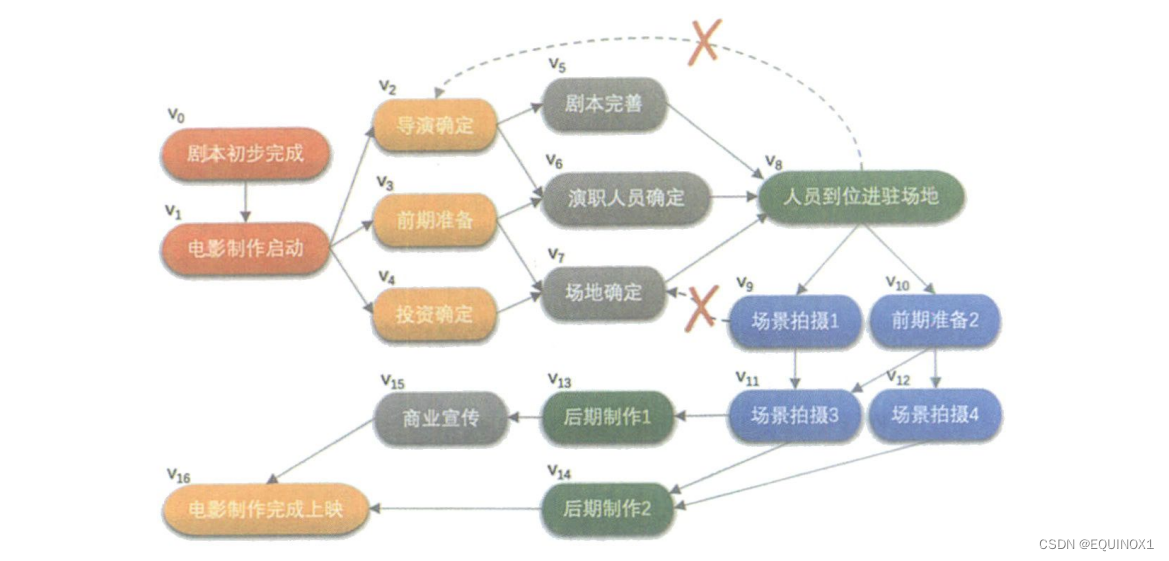
我们会把施工过程、生产流程、软件开发、教学安排等都当成- -个项目工程来对待,所有的工程都可分为若干个“活动”的子工程。例如下图是我这非专业人士绘制的一张 电影制作流程图,现实中可能并不完全相同,但基本表达了一个工程和若干个活动的概念。在这些活动之间,通常会受到一定的条件约束,如其中某些活动必须在另一些活动完成之后才能开始。就像电影制作不可能在人员到位进驻场地时,导演还没有找到,也不可能在拍摄过程中,场地都没有。这都会导致荒谬的结果。因此这样的工程图,一定是无环的有向图。
在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称为AOV网( Activity On Vertex Network)。
AOV网中的弧表示活动之间存在的某种制约关系。比如演职人员确定了,场地也联系好了,才可以开始进场拍摄。另外就是AOV网中不能存在回路。刚才已经举了例子,让某个活动的开始要以自己完成作为先决条件,显然是不可以的。
拓扑序列
设G=(V,E)是一一个具有n个顶点的有向图,V中的顶点序列v1v2…vn,满足若从顶点vi到vj有一条路径, 则在顶点序列中顶点vi必在顶点vj之前。则我们称这样的顶点序列为一个拓扑序列。
拓扑排序算法
所谓拓扑排序,就是对一个有向无环图构造拓扑序列的过程
对AOV网进行拓扑排序的基本思路是:从AOV网中选择一个入度为0的顶点输出,然后删去此顶点,并删除此顶点发出的弧,继续重复此步骤,直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。
显然,对于这种删除一个顶点发出的边的算法,用我们的邻接表会更方便,不过我们要用一个额外的一维数组来存储入度
在算法中,还需要辅助的数据结构----栈, 用来存储处理过程中入度为0的顶点,目的是为了避免每次查找时都要去遍历顶点表找有没有入度为0的顶点。(其实借助队列也可以)
代码实现
vector<V> Topologicalsort()
{
int n = _vertexes.size();
vector<int> degrees(n, 0);
vector<V> ans;
for (int i = 0; i < n; i++)
{
EdgeNode* cur = _LinkTable[i];
while (cur)
{
degrees[cur->_dstIndex]++;
cur = cur->_next;
}
}
stack<int> s;
for (int i = 0; i < n; i++)
if (!degrees[i])
s.push(i);
while (!s.empty())
{
int top = s.top();
s.pop();
ans.push_back(_vertexes[top]);
EdgeNode* cur = _LinkTable[top];
while (cur)
{
if (!(--degrees[cur->_dstIndex]))
s.push(cur->_dstIndex);
cur = cur->_next;
}
}
return ans;
}