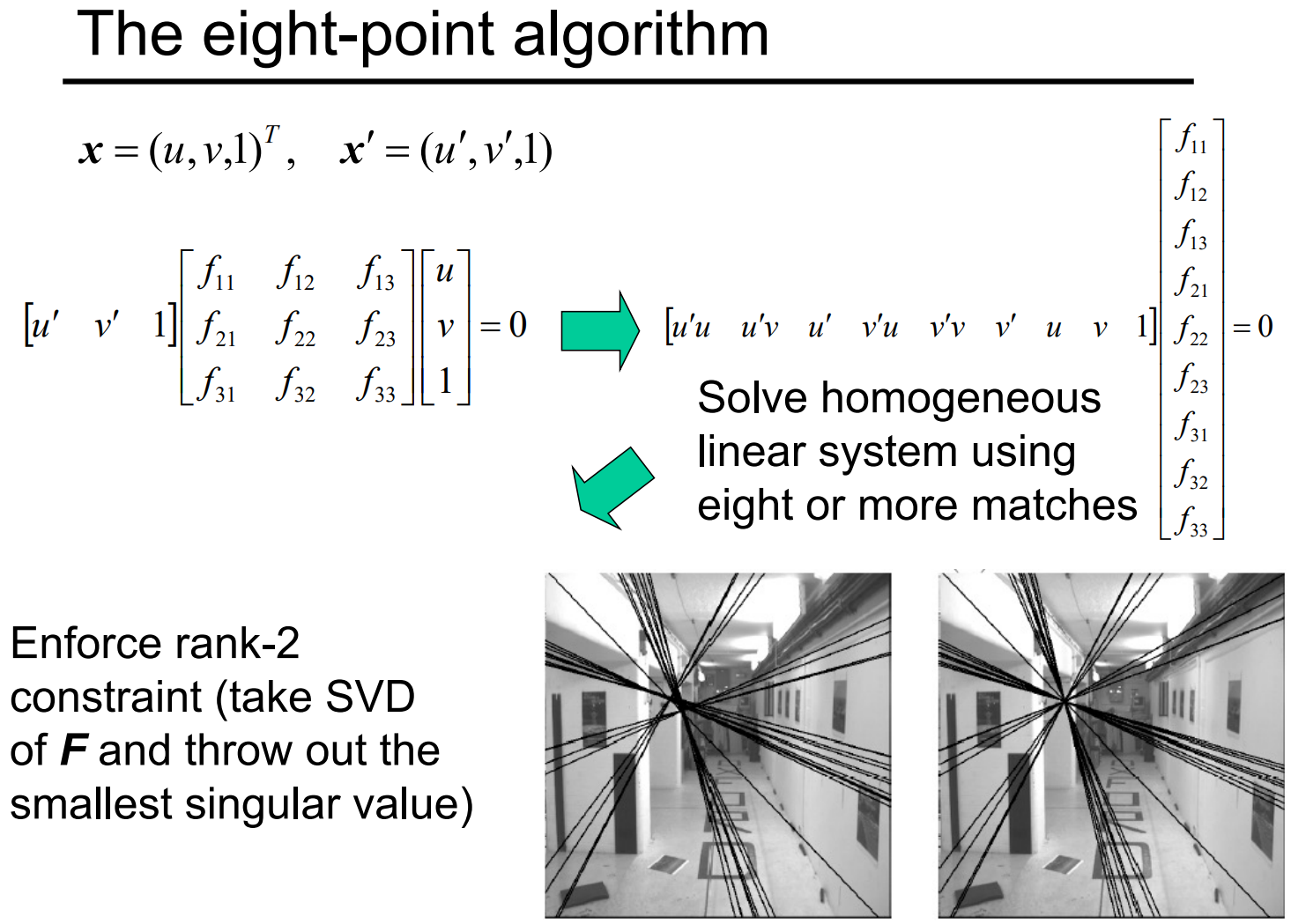
根据前(后)序、中序,确定二叉树,高妙的方法!!!
- 二叉树的前中后序遍历
- ⏩巧妙的方法!
- 根据前序遍历和中序遍历,确定二叉树
- 例题1
- 例题2
- 根据后序遍历和中序遍历,确定二叉树
- 例题1❗
- 例题2
- 例题3
只需动动笔画个图,秒画二叉树~~
声明:本篇文章的技巧适合做选择填空题,编程还得是老路子
–例题全部选自牛客–
二叉树的前中后序遍历
若二叉树为空,则空操作 ->
前序遍历( preorder Travelsal ) :
1️⃣先访问根节点; 2️⃣前序遍历左子树; 3️⃣前序遍历右子树。
中序遍历( inorder Travelsal ) :
1️⃣中序遍历根节点的左子树; 2️⃣访问根节点然后访问根节点; 3️⃣中序遍历右子树。
后序遍历( postorder Travelsal ) :
1️⃣后序遍历左子树; 2️⃣后序遍历右子树; 3️⃣访问根结点。
⏩巧妙的方法!
已知二叉树中的结点有n个
画一组坐标轴(类似小学一年级学的x、y轴),或者想象网格,道理是一样的
step1:
🍎如果是已知前序遍历和中序遍历:
咱们把前序遍历的结果倒序,然后从y轴的1开始,自下而上填在坐标轴上
把中序遍历的结果直接写在x轴的1到n
🍎如果是已知后序遍历和中序遍历:
把后序遍历的结果直接写在y轴的1到n
把中序遍历的结果直接写在x轴的1到n
step2:
将x轴和y轴填入的结点对应,填在第一象限
step3:
按照“自上而下,从左到右”的原则,连接各个结点,二叉树就完美被还原啦!!!
‼️注意 连接各个结点的时候,下层的结点不能 “跨过” 上层的结点,因为这样会改变二叉树中序遍历的次序
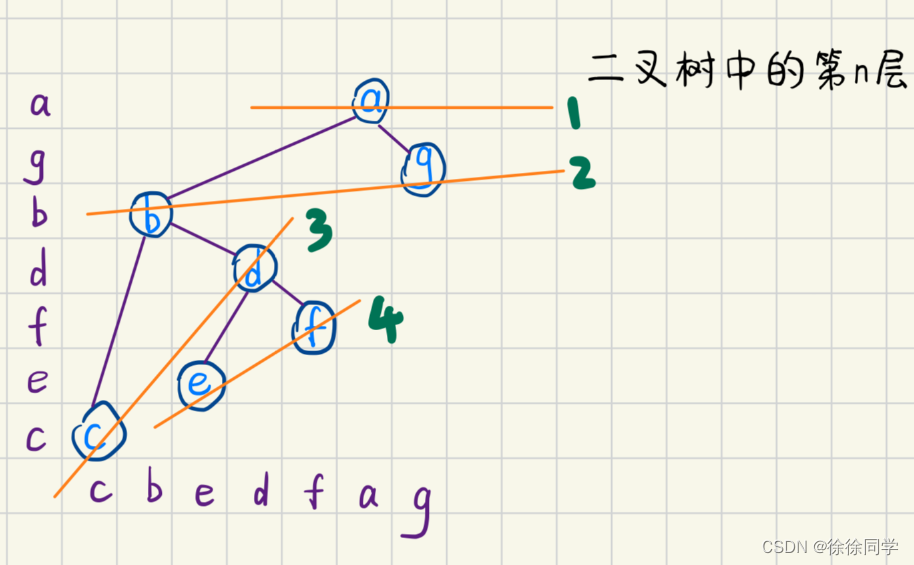
(这里的层指的是坐标系中从上到下的层次,跟树的第n层不是一个概念,我们画的结点所在的层不是真的在二叉树中的层)‼️
比如:
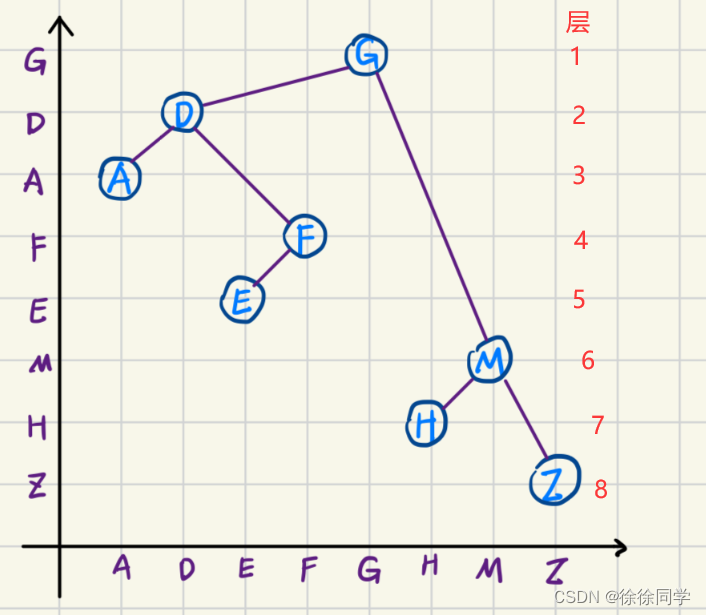
D和M在我们画的图中处于不同的层次,但是他们在二叉树中都处于第二层
根据前序遍历和中序遍历,确定二叉树
上面描述的可能有些抽象,
我们直接上例题,相信大家一眼就能看懂
例题1
 第一步,画图!
第一步,画图!
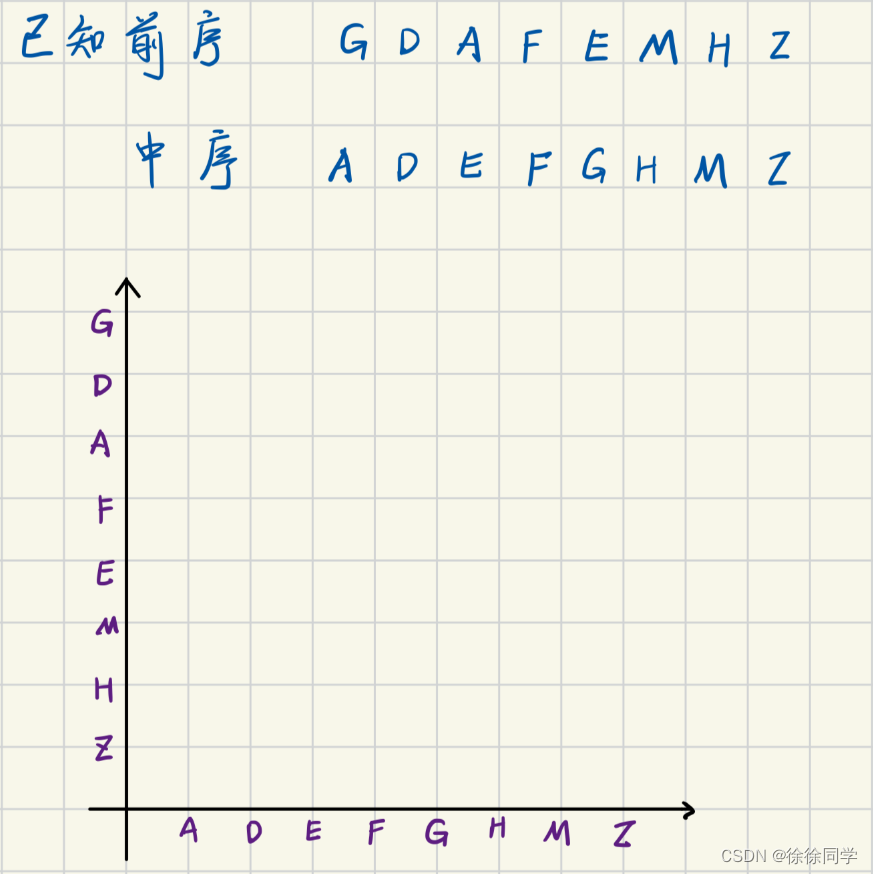
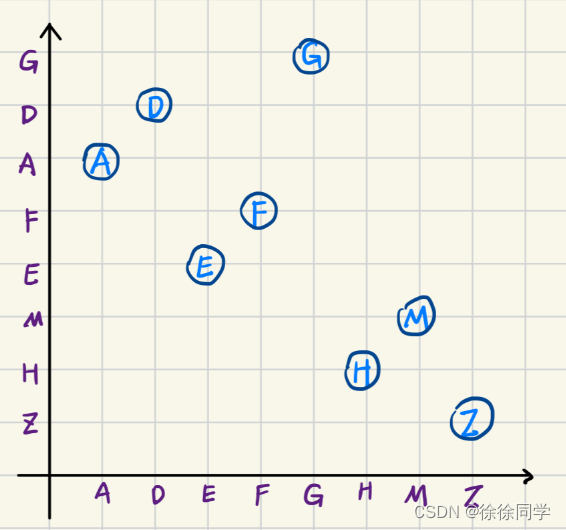
第二步,填上结点!
第三步,按照“自上而下,从左到右”,画出二叉树

有同学问我,为什么不能这样连接,不是从左到右吗?
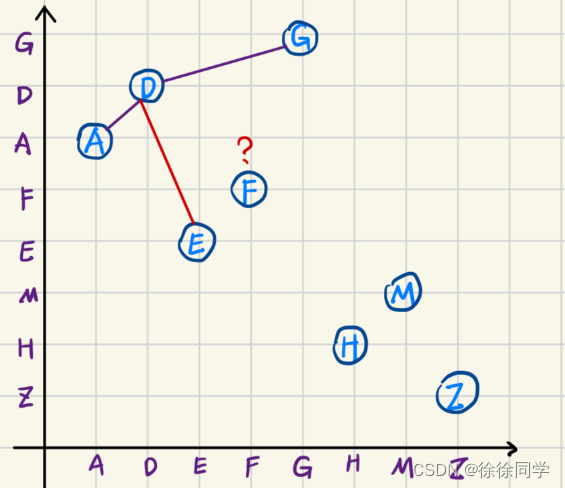
记住第三步的原则:“自上而下,从左到右”‼️要先搞定上下的顺序,再搞定左右顺序
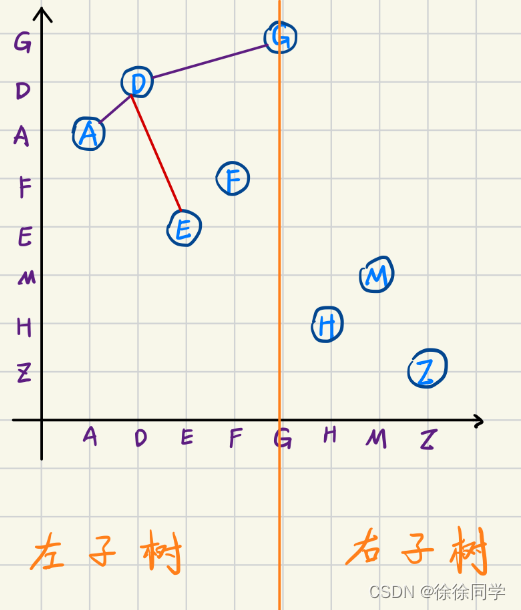
(下图原理就是根据前序遍历中的第一个结点就是根结点,再在中序里确定根结点左边的结点是左子树的结点,右边是右子树的结点)
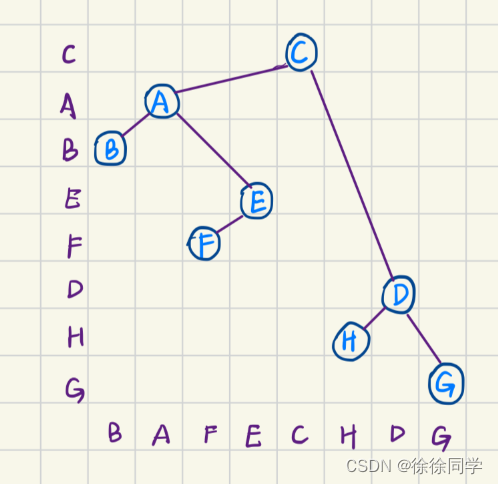
例题2
 好像跟上面的一样,嘿嘿
好像跟上面的一样,嘿嘿
根据后序遍历和中序遍历,确定二叉树
例题1❗
 照葫芦画瓢~~
照葫芦画瓢~~
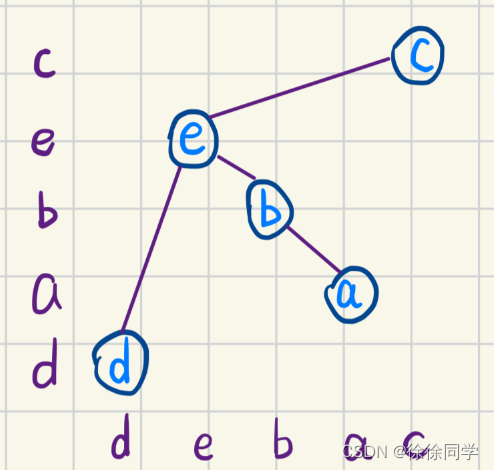
但是这里有个问题,有同学可能要问了,“你不是说自上而下从左到右”吗,我也没违反这个原则,这里为什么不能这样画呢?
👇
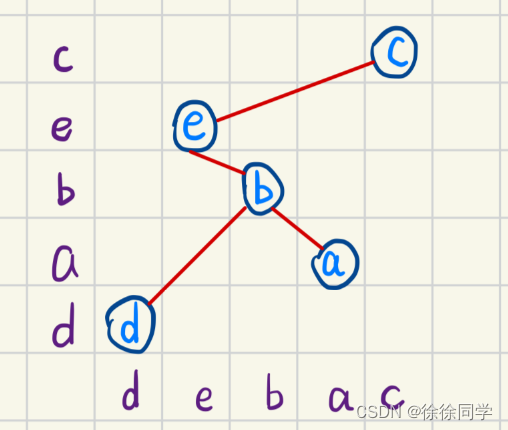
为什么呢?因为这样画中序遍历就麻烦了,跟题目的不一样了,题目给的中序遍历结果是debac,要是像这样画中序遍历就变成edbac了,当然不能这样画
–⏩巧妙的方法!最后的注意,讲的就是这种情况
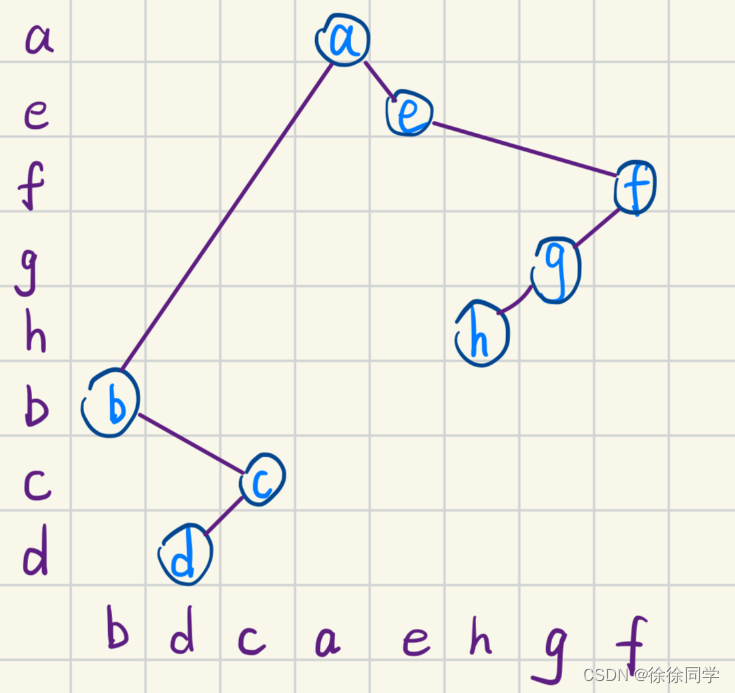
例题2

例题3
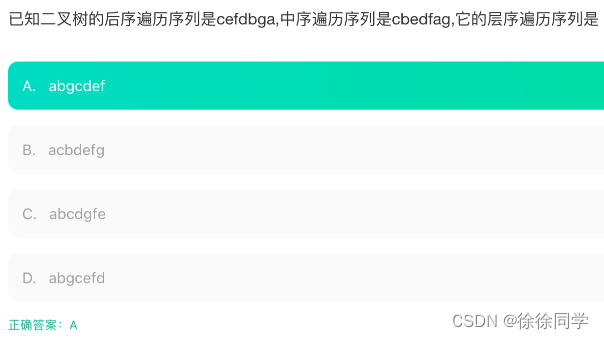 注意这道题求的是层序遍历,不是后序
注意这道题求的是层序遍历,不是后序





![[Linux]线程池](https://img-blog.csdnimg.cn/img_convert/796966d796bdf42634d4542336a0a776.png)