文章目录
- 一、极线约束(Epipolar Constraint)
- 二、相机标定过的情况
- 三、相机没有标定过的情况
- 四、八点算法(eight-point algorithm)
我的《计算机视觉》系列参考UC Berkeley的CS180课程,PPT可以在课程主页看到。
在上一篇文章3D视觉中我们介绍了在两个照相机像平面共面的情况下如何计算深度:深度与景物在图片中的位移成反比。这篇文章我们讨论更一般的情形,像平面不必共面,甚至不必平行。假设两个相机的内参(intrinsics)都是标定(calibrate)过的。
一、极线约束(Epipolar Constraint)
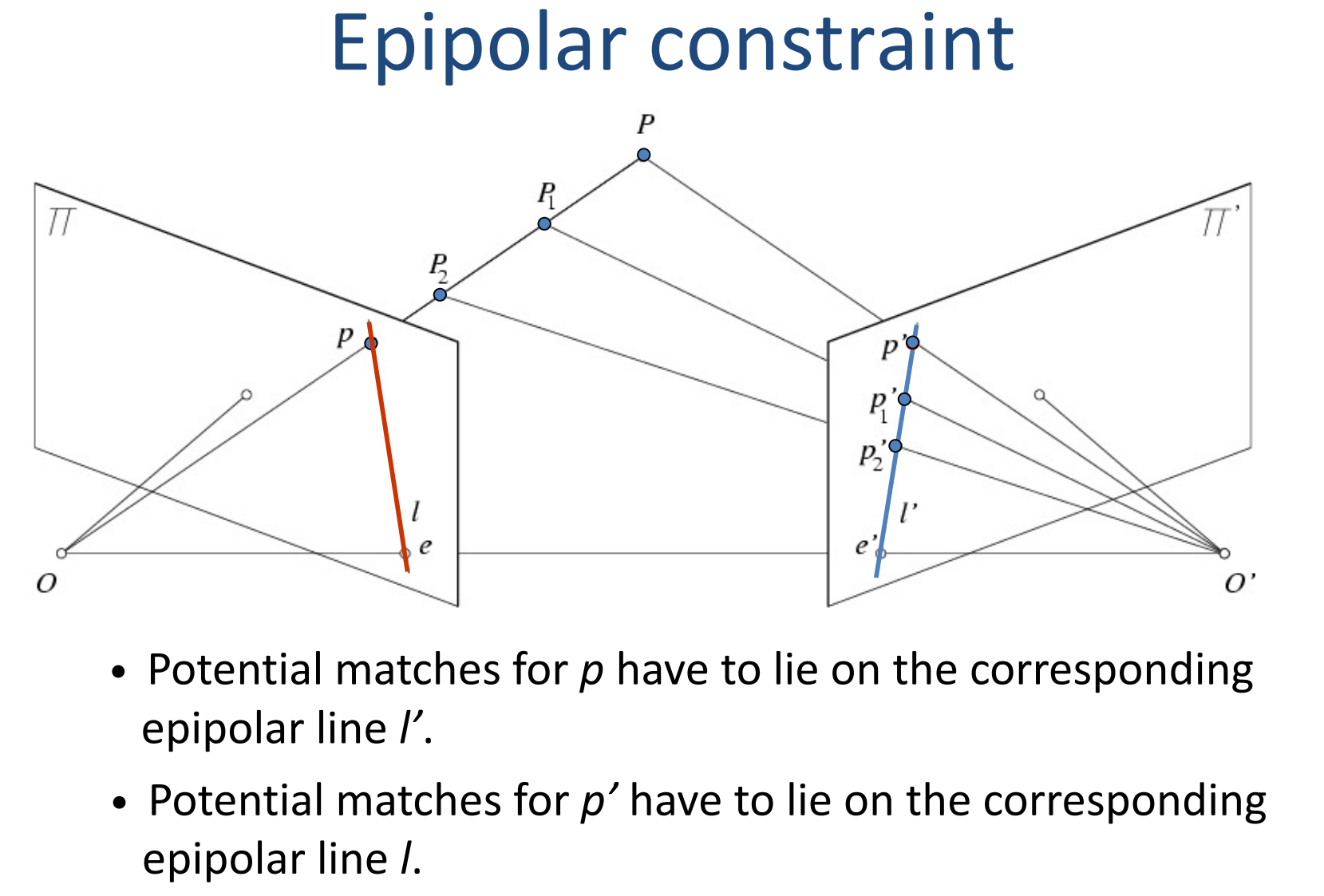
设两个相机的投影中心分别为 O O O和 O ′ O' O′(回想一下投影中心其实可以理解为所有光线都汇聚到的点),两个像平面分别为 Π \Pi Π和 Π ′ \Pi' Π′。设景物在 P P P点, O P OP OP与 Π \Pi Π交于点 p p p,这个 p p p就是景物在像平面 Π \Pi Π上的对应点。知道了 p p p在第一张照片上的坐标,就知道了景物所在的直线——图中的 O P OP OP。现在我们需要在第二张照片上找到景物对应的点。在哪儿找呢?上一篇文章我们讨论的情况中景物一定会出现在一条水平线上。在我们现在讨论的一般情况下,它还是出现在一条直线上吗?答案是肯定的。因为,任取 O P OP OP上的点 P 1 , P 2 , ⋯ P_1,P_2,\cdots P1,P2,⋯,令 O ′ P i O'P_i O′Pi与 Π ′ \Pi' Π′交于 p i ′ p_i' pi′, p i ′ p_i' pi′就是假设景物在 P i P_i Pi点时 其对应于第二张照片上的点。还是那个套路,我们知道 O P i OP_i OPi一定在 由 O P OP OP和 O O ′ OO' OO′确定的平面 O O ′ P OO'P OO′P上,那么 P i P_i Pi在第二张图片上的对应点 p i ′ p_i' pi′也一定在 平面 O O ′ P OO'P OO′P上;而 p ′ p' p′又在平面 Π ′ \Pi' Π′上,所以 p ′ p' p′一定在平面 Π ′ \Pi' Π′和平面 O O P ′ OOP' OOP′的交线上(图中的 l ′ l' l′)。所以,我们寻找 P P P在第二张图片上的对应点时只需要在直线 l ′ l' l′上寻找即可。直线 l l l和 l ′ l' l′称为极线(epipolar lines)。
但我们怎么知道极线 l ′ l' l′在哪里呢?两点确定一条直线,找到 l ′ l' l′上的两个点目前还有些困难,不过找到一个点是可以的。注意到, O O O点也在极线 O P OP OP上,而相机的内参是知道的,也就是说我们知道 O O O点的坐标(相对于 O ′ O' O′而言), O O ′ OO' OO′与 Π ′ \Pi' Π′的交点 e ′ e' e′一定在极线 l ′ l' l′上。 e ′ e' e′连同 O O ′ OO' OO′与 Π \Pi Π的交点 e e e被称为对极点(epipoles);其实就是一个相机看到另一个相机在图片中的位置,它不一定在图片上。当两个相机的像平面共面时,对极点 e e e和 e ′ e' e′就在无穷远处。 O O ′ OO' OO′称为摄影基线(baseline)。包含 O O ′ OO' OO′的所有平面称为极平面(epipolar plane),它绕着 O O ′ OO' OO′旋转;极平面和像平面的交点就是极线,它也绕着 O O ′ OO' OO′旋转。
二、相机标定过的情况
想要找到 l ′ l' l′上的另一个点其实是不可能的——没有另一个点可以找。但是,注意我们的相机是标定过的,我们知道两个相机之间的坐标变换。令点 p p p在第一个相机坐标系下的坐标为 x \boldsymbol{x} x,即 O P → = x \overrightarrow{OP}=\boldsymbol{x} OP=x,再令点 p ′ p' p′在第二个相机坐标系下的坐标为 x ′ \boldsymbol{x}' x′。现在我们在第二个相机坐标系(即 O ′ O' O′坐标系)下讨论问题。向量 x \boldsymbol{x} x就不能直接使用了,需要转换到 O ′ O' O′坐标系: x O = R x + t \boldsymbol{x}_O=R\boldsymbol{x}+\boldsymbol{t} xO=Rx+t,其中 R R R是旋转矩阵, t = O O ′ → \boldsymbol{t}=\overrightarrow{OO'} t=OO′是平移向量。我们还知道, x , x ′ , t \boldsymbol{x},\boldsymbol{x}',\boldsymbol{t} x,x′,t是共面的,即 x ′ ⋅ ( t × x O ) = 0 \boldsymbol{x}'\cdot(\boldsymbol{t}\times\boldsymbol{x}_O)=0 x′⋅(t×xO)=0其中 t × x \boldsymbol{t}\times\boldsymbol{x} t×x是极平面的法向量, x ′ \boldsymbol{x}' x′与其点积为 0 0 0说明与其垂直,进而说明 x ′ \boldsymbol{x}' x′在极平面上。化简: t × x O = t × ( R x + t ) = t × R x + x × t = t × R x + 0 = t × R x \boldsymbol{t}\times\boldsymbol{x}_O=\boldsymbol{t}\times (R\boldsymbol{x}+\boldsymbol{t})=\boldsymbol{t}\times R\boldsymbol{x}+\boldsymbol{x}\times \boldsymbol{t}=\boldsymbol{t}\times R\boldsymbol{x}+\boldsymbol{0}=\boldsymbol{t}\times R\boldsymbol{x} t×xO=t×(Rx+t)=t×Rx+x×t=t×Rx+0=t×Rx因此有 x ′ ⋅ ( t × R x ) = 0 \boldsymbol{x}'\cdot(\boldsymbol{t}\times R\boldsymbol{x})=0 x′⋅(t×Rx)=0叉乘可以转化成与一个反对称矩阵 [ t × ] [\boldsymbol{t}_\times] [t×]的乘法:
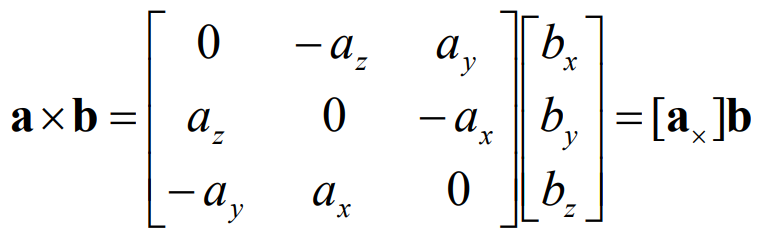
故等式化为 x ′ T [ t × ] R x = 0 \boldsymbol{x}'^T[\boldsymbol{t}_\times]R\boldsymbol{x}=0 x′T[t×]Rx=0。令 E = [ t × ] R E=[\boldsymbol{t}_\times]R E=[t×]R,则有 x ′ T E x = 0 \boldsymbol{x}'^TE\boldsymbol{x}=0 x′TEx=0这就是Longuet-Higgins方程。 E E E被称为本质矩阵(Essential Matrix)。
其实, E x E\boldsymbol{x} Ex就表示极线 l ′ l' l′。设 l ′ l' l′在像平面上的方程为 a x ′ + b y ′ + c = 0 ax'+by'+c=0 ax′+by′+c=0,即 [ a , b , c ] [ x ′ , y ′ , 1 ] T = 0 [a,b,c][x',y',1]^T=0 [a,b,c][x′,y′,1]T=0。注意像平面 Π ′ \Pi' Π′的法向量和 O ′ O' O′坐标系下的 z z z轴平行(即 Π ′ \Pi' Π′与 x ′ O y ′ x'Oy' x′Oy′面平行),所以 x ′ , y ′ x',y' x′,y′既是 O ′ O' O′坐标系下的横纵坐标,也是像平面坐标系下的横纵坐标。那么 a , b , c a,b,c a,b,c就可以用 E x E\boldsymbol{x} Ex来确定了。
最后, E E E是奇异矩阵,秩为 2 2 2,有五个自由度:3个平移,2个旋转(平面绕法线旋转等于没旋转,所以少一个旋转自由度)。
三、相机没有标定过的情况
设图像上的坐标为 ( u , v ) (u,v) (u,v),令 x ^ = [ u , v , 1 ] T \hat{\boldsymbol{x}}=[u,v,1]^T x^=[u,v,1]T。令 K K K和 K ′ K' K′分别是连哥哥相机的 3 × 3 3\times 3 3×3版本的内参矩阵(intrinsic matrix),则 x = K − 1 x ^ \boldsymbol{x}=K^{-1}\hat{\boldsymbol{x}} x=K−1x^, x ′ = K ′ − 1 x ^ ′ \boldsymbol{x}'=K'^{-1}\hat{\boldsymbol{x}}' x′=K′−1x^′,代入 x ′ T E x = 0 \boldsymbol{x}'^TE\boldsymbol{x}=0 x′TEx=0得 x ^ ′ T ( K ′ − 1 ) T E K − 1 ⏟ F x ^ = 0 \hat{\boldsymbol{x}}'^T\underset{F}{\underbrace{{(K'^{-1})}^TEK^{-1}}}\hat{\boldsymbol{x}}=0 x^′TF (K′−1)TEK−1x^=0其中 F = ( K ′ − 1 ) T E K − 1 F={(K'^{-1})}^TEK^{-1} F=(K′−1)TEK−1称为基础矩阵(Fundamental Matrix)。它也是秩为2的矩阵,有7个自由度:秩为2相当于多一个方程,损失一个自由度;把 F F F放大若干倍等式不变,再损失一个自由度。
四、八点算法(eight-point algorithm)
如何求得基础矩阵 F F F呢?还是老套路,线性回归。给定两张图片上的8个点对,代入方程 x ^ ′ T F x ^ = 0 \hat{\boldsymbol{x}}'^T F\hat{\boldsymbol{x}}=0 x^′TFx^=0用最小二乘法求得最优的 F F F即可。
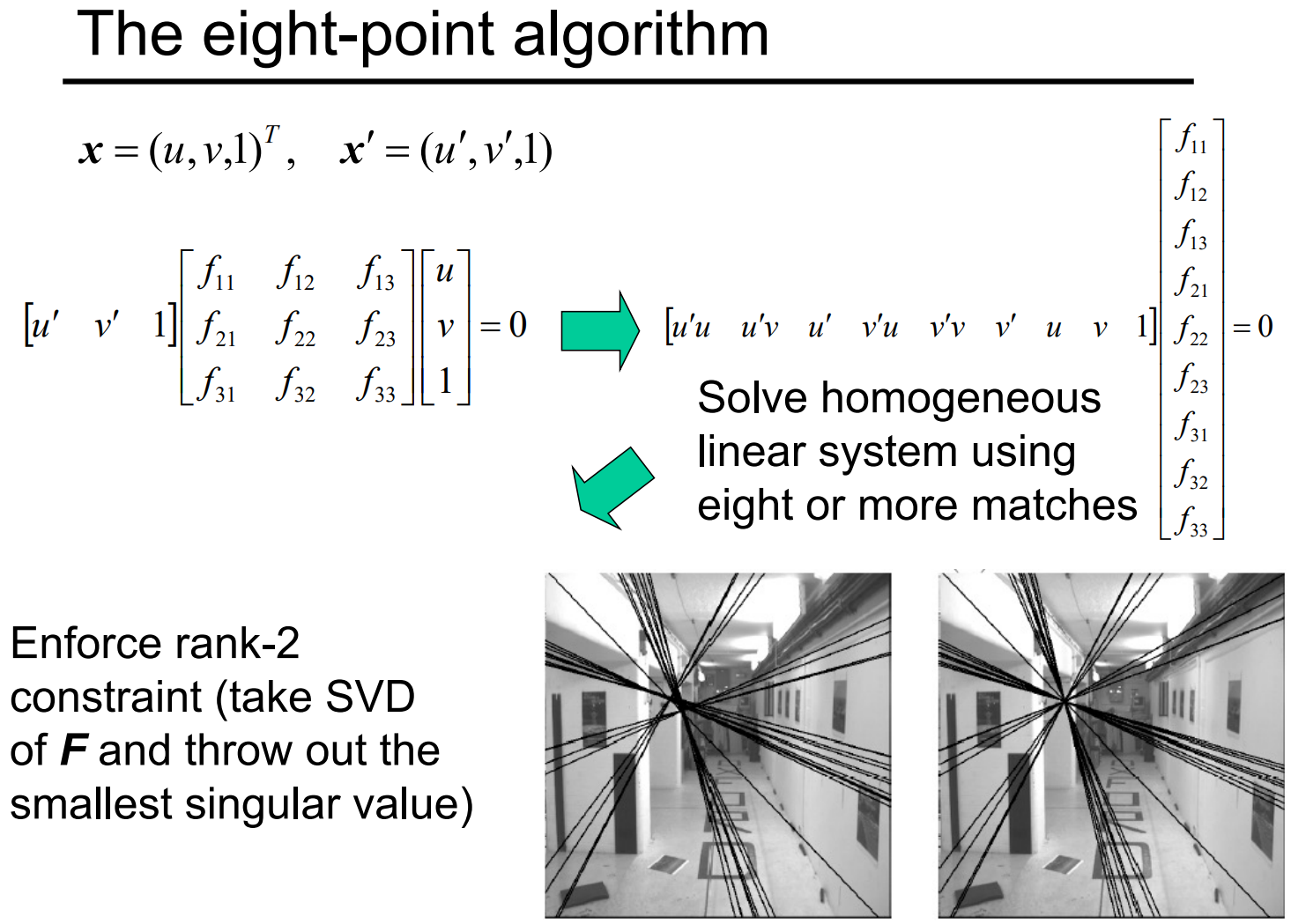
用 8 8 8个点是利用到了秩为 2 2 2的约束,少了一个自由度;另外一个缺失的自由度没必要利用,因为没必要手动确定 F F F的缩放大小。实践中应该用多于 8 8 8个点。
最后,如果我们标定了相机,那么就可以从 F F F求得 E E E;而 E E E又可以进行奇异值分解最终还原 R R R和 t \boldsymbol{t} t。过程比较复杂,可以参考https://inst.eecs.berkeley.edu/~ee290t/fa19/lectures/lecture10-3-decomposing-F-matrix-into-Rotation-and-Translation.pdf。