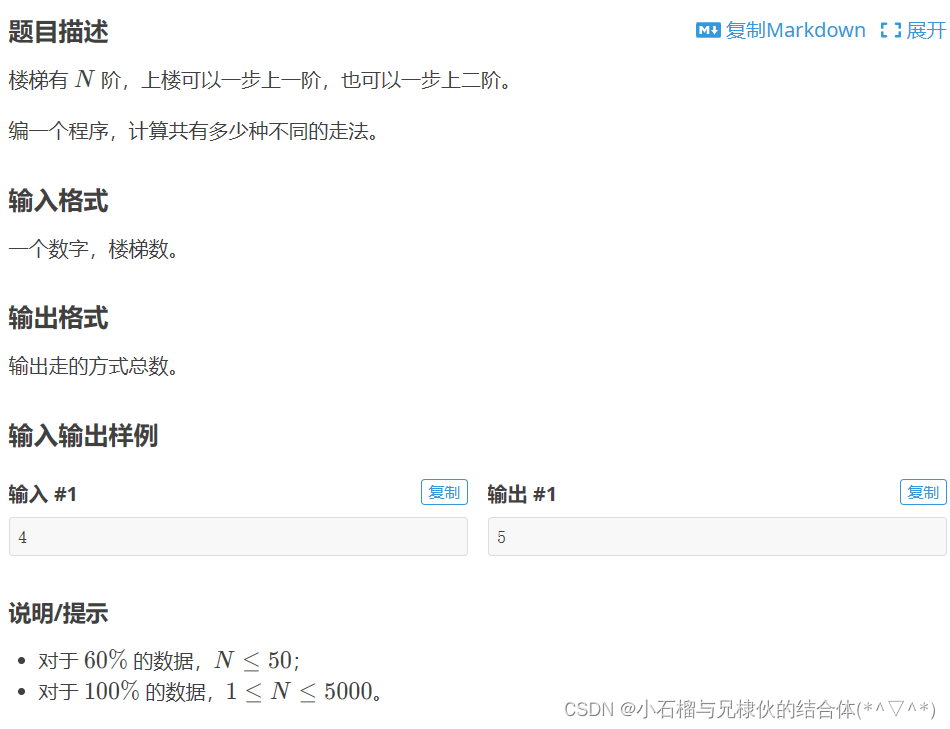
C++ 动态规划 DP教程 (一)思考过程(*/ω\*)
news2026/2/11 16:23:51
思路:
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1146824.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【0基础学Java第三课】-- 运算符
3. 运算符 3.1 什么是运算符3.2 算术运算符3.2.1 **基本四则运算符:加减乘除模( - * / %)**3.2.2 增量运算符 - * %3.2.3 自增/自减运算符 -- 3.3 关系运算符3.4逻辑运算符(重点)3.4.1 逻辑与 &&3.4.2 逻辑 ||3.4.3逻辑非 !3.4.4 短路求值 3.5 …
Lauterbach使用指南之RunTime功能
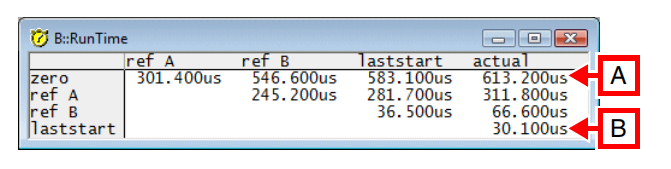
Lauterbach使用指南之RunTime功能 前言
首先,请问大家几个小小问题,你清楚:
Lauterbach这个工具是干什么用的吗?在软件运行过程中如何测量两个运行point之间的runtime时间呢?Lauterbach的RunTime功能具体应当如何来操…
Linux中shell脚本的基础知识
目录
一、shell脚本的意义
二、如何创建shell脚本
三、如何执行shell脚本
四、如何对脚本进行调试
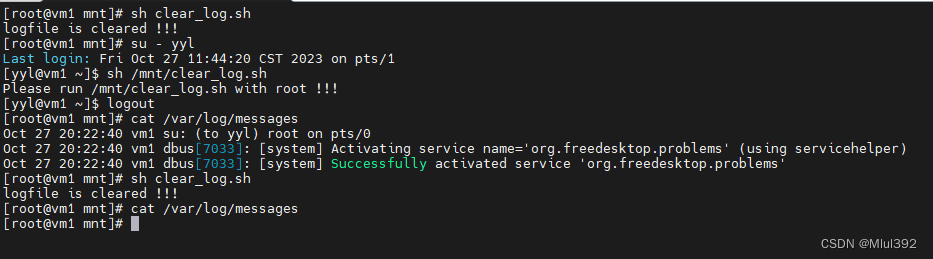
五、练习 一、shell脚本的意义
1、shell:脚本中命令的解释器 2、脚本的意义:
记录命令执行的过程和执行逻辑,以便以后重复执行脚本可以…
matlabR2021a正版免费使用
目录 matlab介绍:
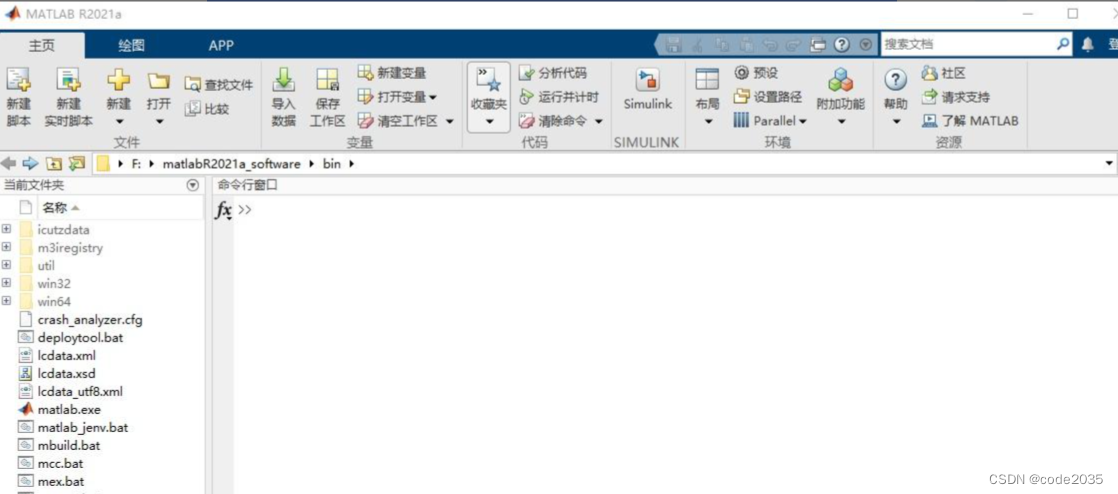
安装: matlab介绍:
MATLAB(Matrix Laboratory的缩写)是一种高级技术计算和编程环境,由MathWorks公司开发。它在科学、工程、数据分析和数学建模领域中广泛应用,为用户提供了…
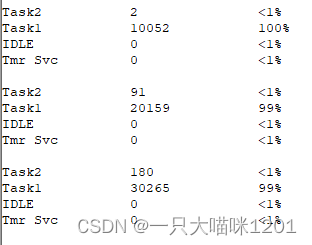
【RTOS学习】互斥管理 | 调试 | 信息统计
🐱作者:一只大喵咪1201 🐱专栏:《RTOS学习》 🔥格言:你只管努力,剩下的交给时间! 互斥管理 | 调试 | 信息统计 🍉互斥管理🌰屏蔽中断🌰暂停调度器…
VMware Horizon 8 2309 Enterprise虚拟桌面
VMware Horizon 8 2309 Enterprise虚拟桌面 一、虚拟桌面二、产品发布三、VMware Horizon 8 2309 Enterprise1.VMware Horizon 8 2309 Enterprise产品清单2.安装部署3. 优化工具总结 一、虚拟桌面
利用虚拟桌面和应用随时随地进行访问。
从云端进行管理 使用云端控制台和 Saa…
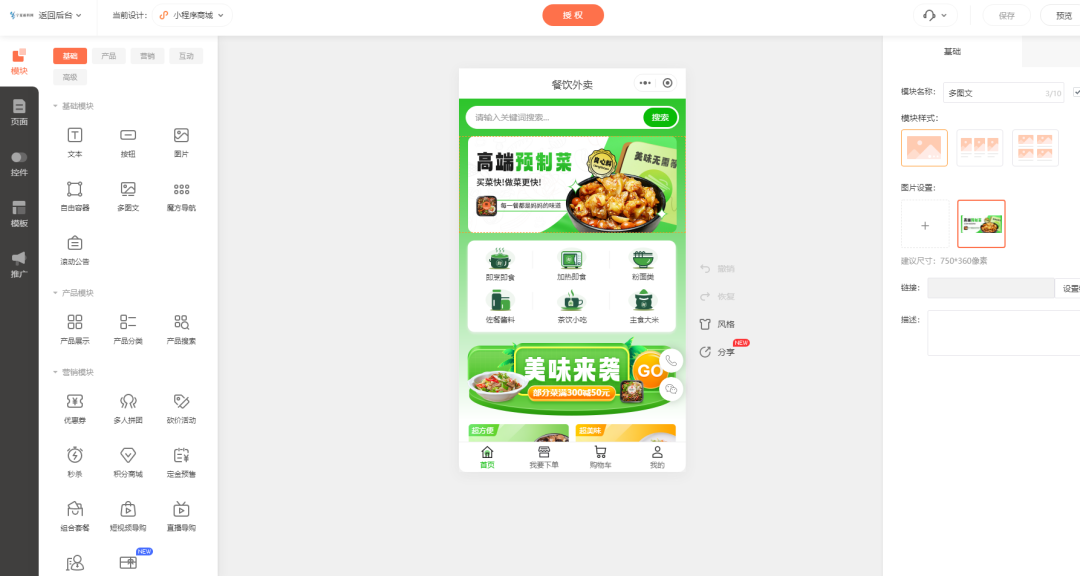
预制菜配送小程序商城的效果如何
预制菜是近些年热度较高的新赛道,很多商家品牌入局,而投入到市场中也受到不少商家的喜欢,各种品牌和经销商层出不穷,目前各品牌主要以拓展市场和研究菜品为主,而线上无疑是很好的宣传销售渠道。
接下来让我们看看通过…
Docker Consul概述及构建
Docker Consul概述及构建 一、Consul概述1.1、什么是Consul1.2、consul 容器服务更新与发现1.3、服务注册与发现的含义1.4、consul-template概述1.5、registrator的作用 二、consul部署2.1、环境配置2.2、在主节点上部署consul2.3 、配置容器服务自动加入nginx集群2.3.1、安装G…
【Linux】:进程程序替换
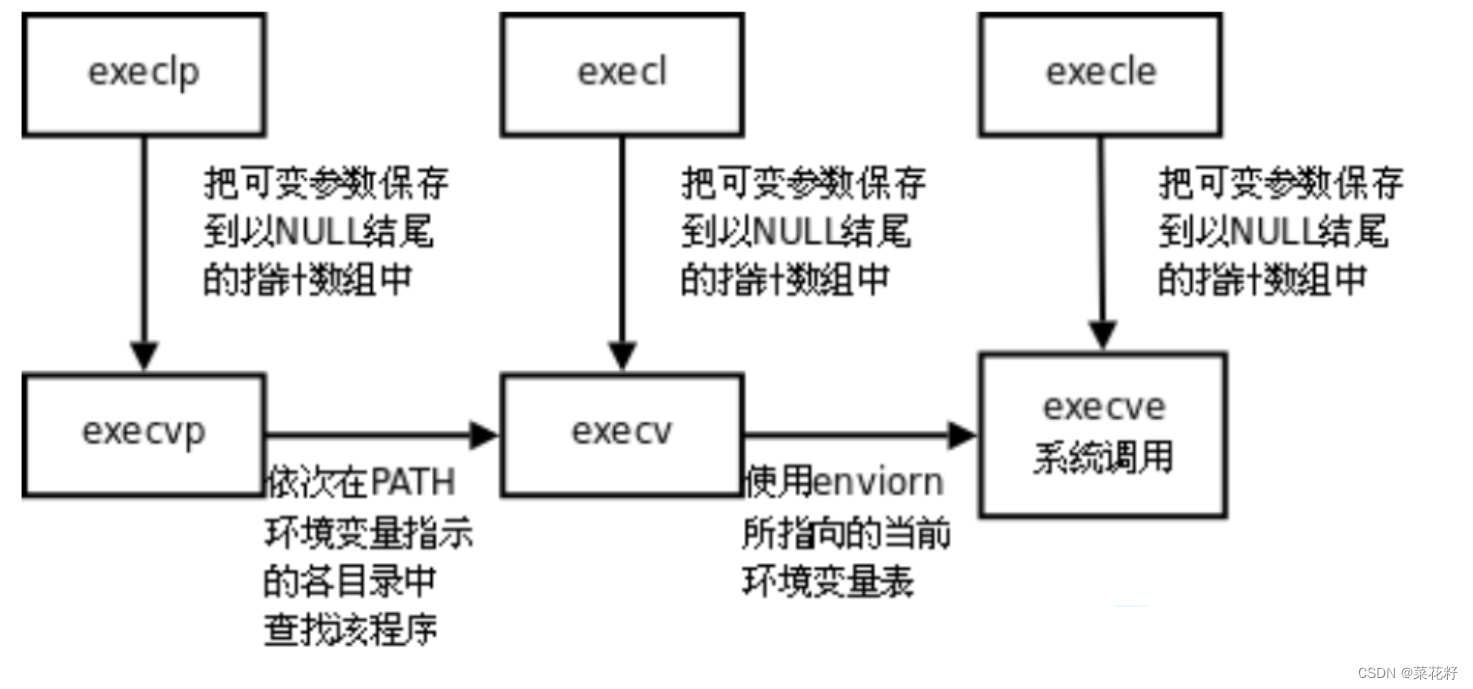
进程程序替换 一.替换原理二.替换函数三.exec类函数 一.替换原理 用fork创建子进程后执行的是和父进程相同的程序(但有可能执行不同的代码分支),子进程往往要调用一种exec函数以执行另一个程序。当进程调用一种exec函数时,该进程的用户空间代码和数据完全…
CleanMyMac X2024永久免费版mac电脑管家
日常使用中,很多用户忽略了Mac清除数据的重要性。当Mac运行速度越来越慢,发热严重,储存空间总是不足的时候,才意识到保持日常清理才是解决这些问题的根本。经常清理Mac,还有你意想不到的好处。
提高系统性能ÿ…
React-快速搭建开发环境
1.安装
说明:react-excise-01是创建的文件名 npx create-react-app react-excise-01 2. 打开文件
说明:we suggest that you begin by typing:下面即是步骤。 cd react-excise-01 npm start 3.显示
HIT_OS_LAB1 调试分析 Linux 0.00 引导程序
操作系统实验一
姓名:董帅学号:2021111547班级:21R0312
1.1 实验目的
熟悉实验环境掌握如何手写Bochs虚拟机的配置文件掌握Bochs虚拟机的调试技巧掌握操作系统启动的步骤
1.2 实验内容
1.2.1 掌握如何手写Bochs虚拟机的配置文件 boot: f…
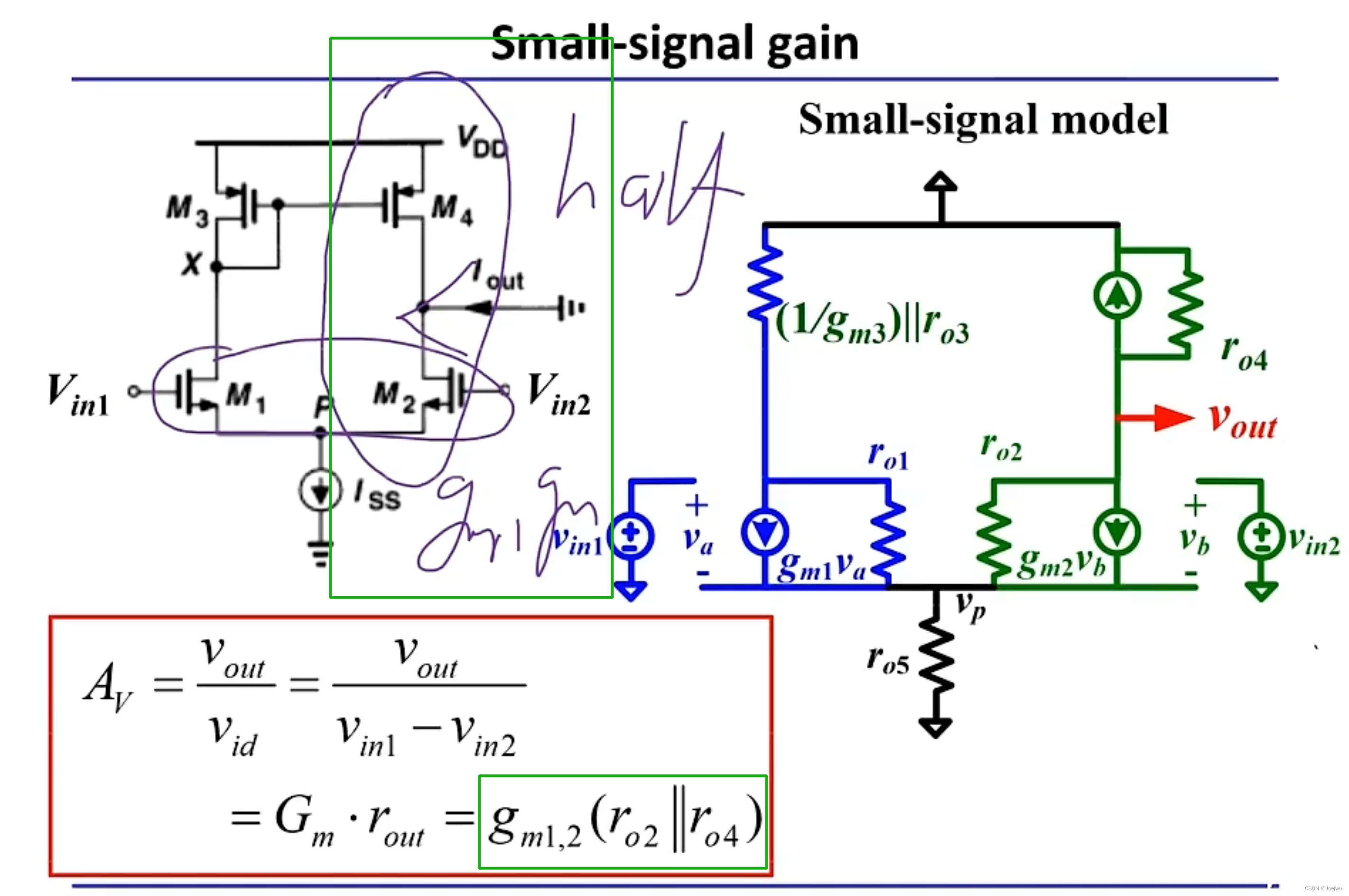
拉扎维模拟CMOS集成电路设计西交张鸿老师课程P10~13视频学习记录
---------------------------------------------------------------------------------------------------------------------------------
p10
短沟道,除了沟长调,还可能出现速度饱和问题;
但是在拉扎维这本书里面没有考虑这个问题&#…
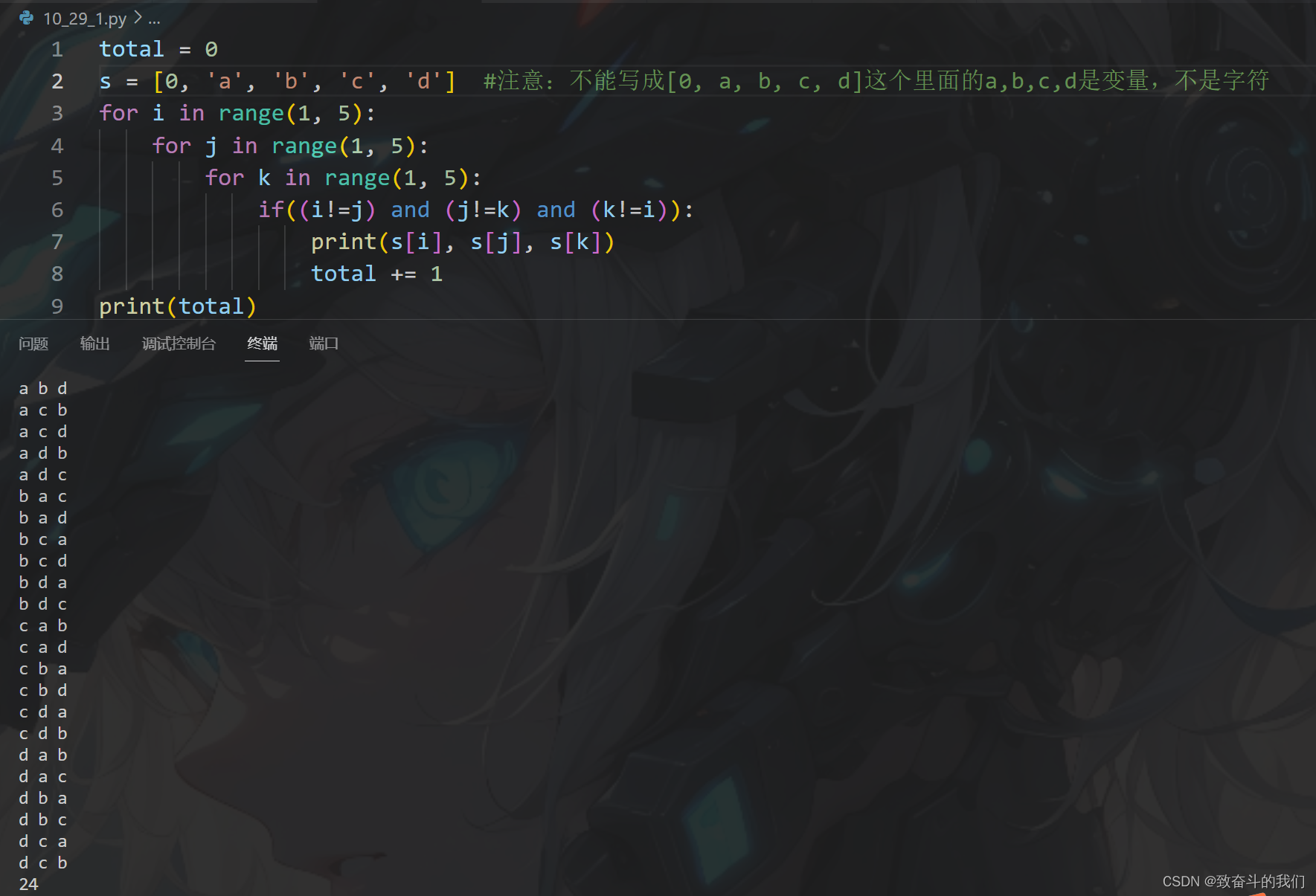
python随手小练12(南农作业题)
题目: 设有四个字母:a bcd,能组成多少个互不相同且无重复数字的三个字母的单词?各是什么? 解题思路:遍历全部可能的组合,把有重复的删除 具体操作:
total 0
s [0, a, b, c, d] #注意:不能写成[0, a, b, c, d]
for i in range(1, 5): …
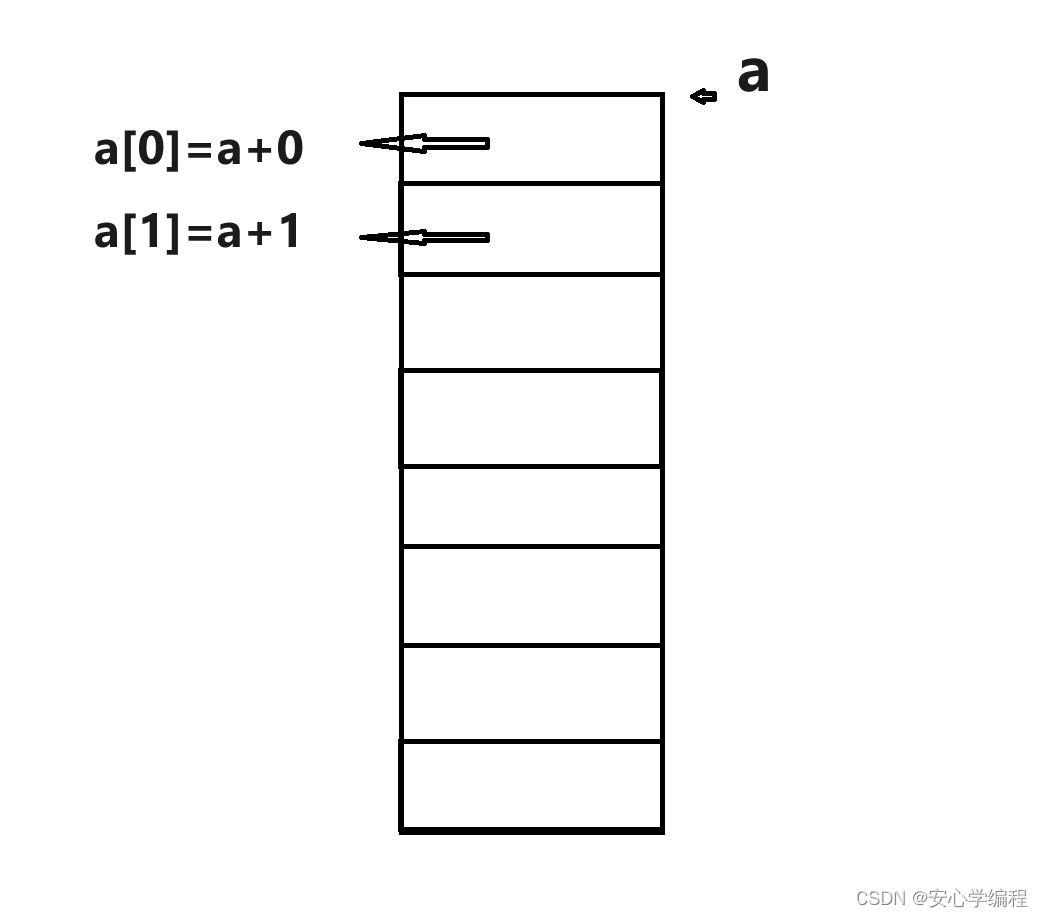
为什么数组的下标是从0开始呢?
我们在许多的编程语言中,大部分的数组下标都是从零开始的,那为什么不是从一开始的呢?
首先我们,先要了解数组相关的定义。
数组(Array)是一种线性表数据结构。它用一组连续的内存空间,来存储一…
关于FTP的一些往事
公司每天都要从美国的服务器下载大量的语音文件。然后根据语音的内容完成相关的医疗报告。不同语音的实时性要求是不一样的,有些要求6小时内完成(TAT6) ,有些则是12小时。中美之间的网速又特别慢,所以,如何…
在vscode中运行c++代码,windows 11系统
缘起
工作中用mac电脑,装了vscode和c,在家里的windows电脑上,也想运行vscode,这时候就遇到问题了。现在将问题解决方案记录下来,以供参考。
解决方案
开始比较懒,直接百度一下,找了几篇文章&…