队列(Queue)概念+通过单、双链表来模拟队列+环形队列+OJ面试题(用队列实现栈、用栈实现队列、设计环形队列)

文章目录

队列(Queue)
- 一、概念
- - 1.尾进头出
- 二、模拟队列
- - 1.单链表实现队列
  - - 1.1 设置结点
    - 1.2 入队offer
    - 1.3出队 poll
    - 1.4 empty方法，peek方法，getUsedSize方法
  - 2.双链表实现队列
  - - 2.1 创建结点
    - 2.2 入队列
    - 2.3 出队列
    - 2.4 peek、size、isEmpty方法
- 三、环形队列
- - 1. 环形队列一般用数组实现
  - 2.判断数组是否满了的方法：
  - 3.下标循环
  - 4、双端队列(Deque)
- 四、队列的使用
- 五、OJ题
- - 1.设计循环队列
  - - 1.1 思路
    - 1.2 代码
  - 2.用队列实现栈
  - - 2.1 思路
    - 2.2 图解
    - 2.1 代码
  - 3.用栈实现队列
  - - 3.1 思路
    - 3.2 图解
    - 3.3 代码

队列(Queue)

一、概念

与栈相反，队列就像食堂排队买饭一样，排好队后，第一个来的人，先买饭，后来的人后买，依次从队尾排到队头，离开的时候，买好饭的人从队头离开
或者可以这么理解：队列就是挤牙膏，出去的都是前面的，后面的挤向前面
队列和栈一样，可以使用数组实现也可以使用链表实现

1.尾进头出

队列只能在一段进行插入数据，在另一端进行删除的特殊线性表。
尾进头出：先进先出，后进后出。
插入的一端叫队尾，删除的一端叫队头。

二、模拟队列

1.单链表实现队列

普通单链表：
加last结点

入队列: 头插法 o（1）
出队列：删除链表中的最后一个结点 o(n)

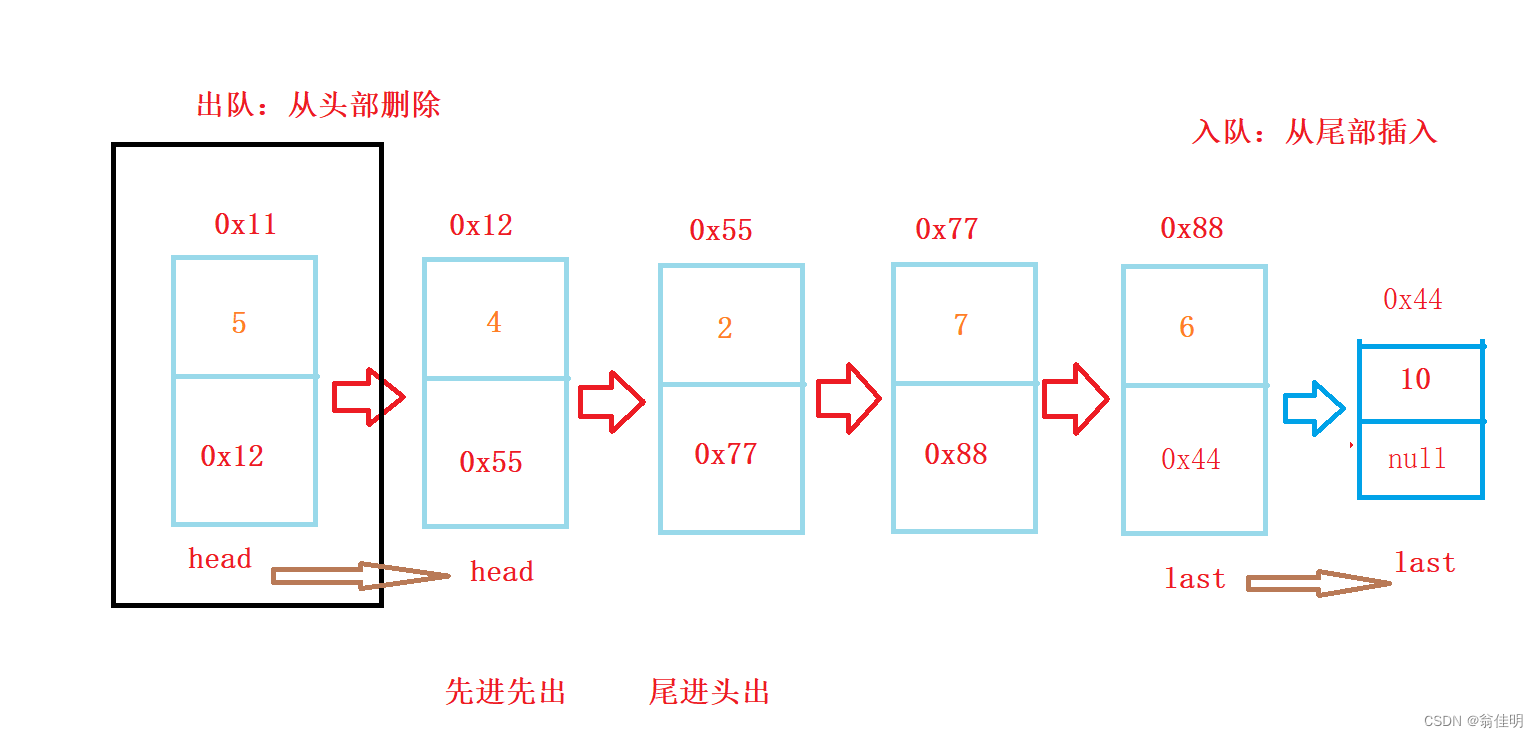
用last记录尾结点来改进：

入队：从尾结点插入 o(1)
出队：从头结点删除 o(1)

局限：只能从尾部插入，头部删除，但是双链表没有限制

1.1 设置结点

public class MyQueue {//单链表实现队列
    static class Node {
        public int val;
        public Node next;
        public Node(int val) {
            this.val = val;
        }
    }
    public int usedSize;
    public Node Last;
    public Node Head;

设置头尾结点，使用大小

1.2 入队offer

public void offer(int val) {//入队
        Node node = new Node(val);
        if (Head == null) {//当头结点为空时
            Head = node;
            Last = node;
        } else {
            Last.next = node;//尾插
            Last = node;//Last后移
        }
        usedSize++;
    }

当头结点为空时，头尾结点都是node
否则进行尾插法，List结点后移

1.3出队 poll

public int poll() {//出队
        if (empty()) {
            return -1;
        }
        int val = Head.val;
        Head = Head.next;
        if (Head==null){
            Last = null;//只剩一个结点
        }
        usedSize--;
        return val;
    }

1.判断是否为空
2.记录头结点的值
3.头结点后移一位，如果移位后的头结点为空，则Last也要置为空
4.返回记录的val

1.4 empty方法，peek方法，getUsedSize方法

  public boolean empty() {
        return usedSize == 0;
    }
    public int peek(){
        if (empty()){
            return -1;
        }
        return Head.val;
    }
   public int getUsedSize(){
        return usedSize;
    }

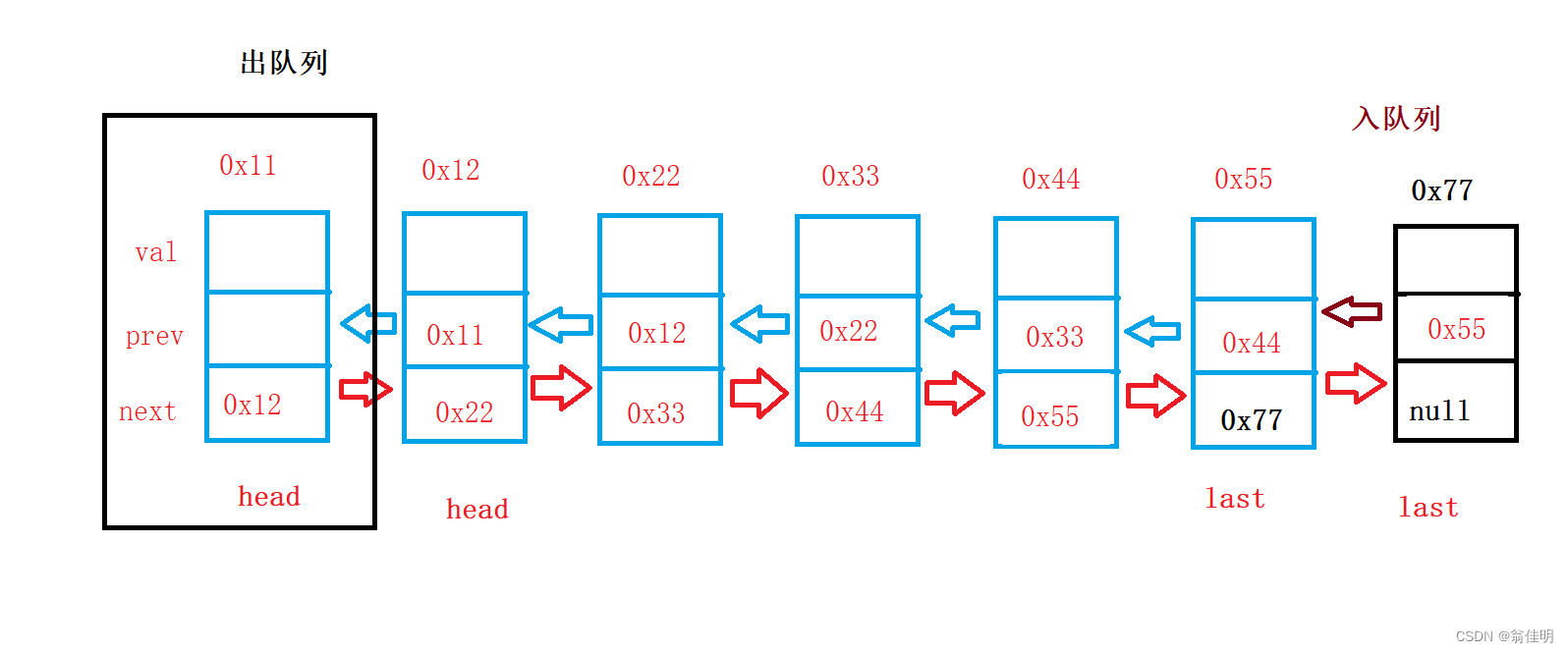
2.双链表实现队列

两端都可以出入，并且时间复杂度都是o(1)
-

2.1 创建结点

public class MyQueue1 {
    public static class ListNode {
        ListNode next;
        ListNode prev;
        int val;

        public ListNode(int val) {
            this.val = val;
        }
    }

    ListNode head;
    ListNode last;
    int size = 0;

创建头尾结点，构造方法，长度大小

2.2 入队列

   public void offer(int data) {
        ListNode node = new ListNode(data);
        if (head == null) {
            head = node;
        } else {
            last.next = node;
            node.prev = last;
        }
        last = node;
        size++;
    }

当头结点为空的时候，头尾结点都是node
不为空，在尾部插入，尾结点后移，长度加一

2.3 出队列

 public int poll() {
        int val = 0;
        if (head == null) {
            return -1;
        } else if (head == last) {
            val = head.val;
            head = null;
            last = null;
        } else {
            val = head.val;
            head = head.next;
            head.prev.next = null;
            head.prev = null;
        }
        size--;
        return val;
    }

val记录要返回的值
如果头结点为空，不能删除，返回-1
只有一个结点，取出val，头尾结点置空
否则，删除头结点，返回头结点的值，长度减一；
当然，也可以头结点入队，尾结点出队

2.4 peek、size、isEmpty方法

 public int peek() {
        if (head == null) {
            return -1;
        }
        return head.val;
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return head == null;
    }

同上

三、环形队列

1. 环形队列一般用数组实现

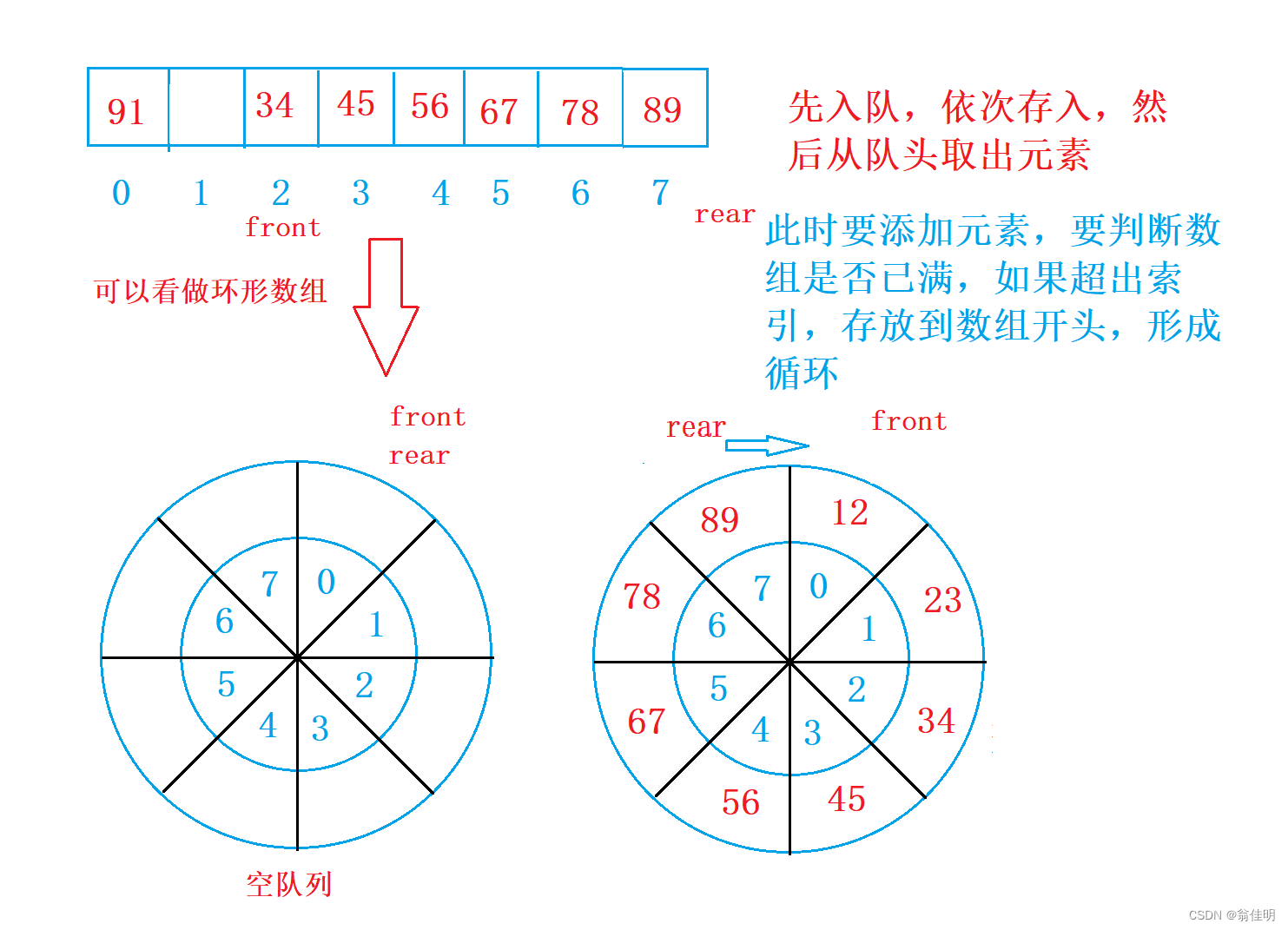
在这里插入图片描述

1.因为要循环的进入队列，我们把数组看成一个环形的结构
2.我们在进队时要考虑数组是否满了

2.判断数组是否满了的方法：

1.使用usedsize,每次进队出队改变usedsize的大小，当usedsize等于数组的长度时说明已经存满
2.使用标记，空的为false,判断要添加的位置是否为空，如果进队，标记为true，出队标记为false
3.牺牲一个空间，来表示已经存满，判断rear的下一个是不是front，是front证明满了

在这里插入图片描述

3.下标循环

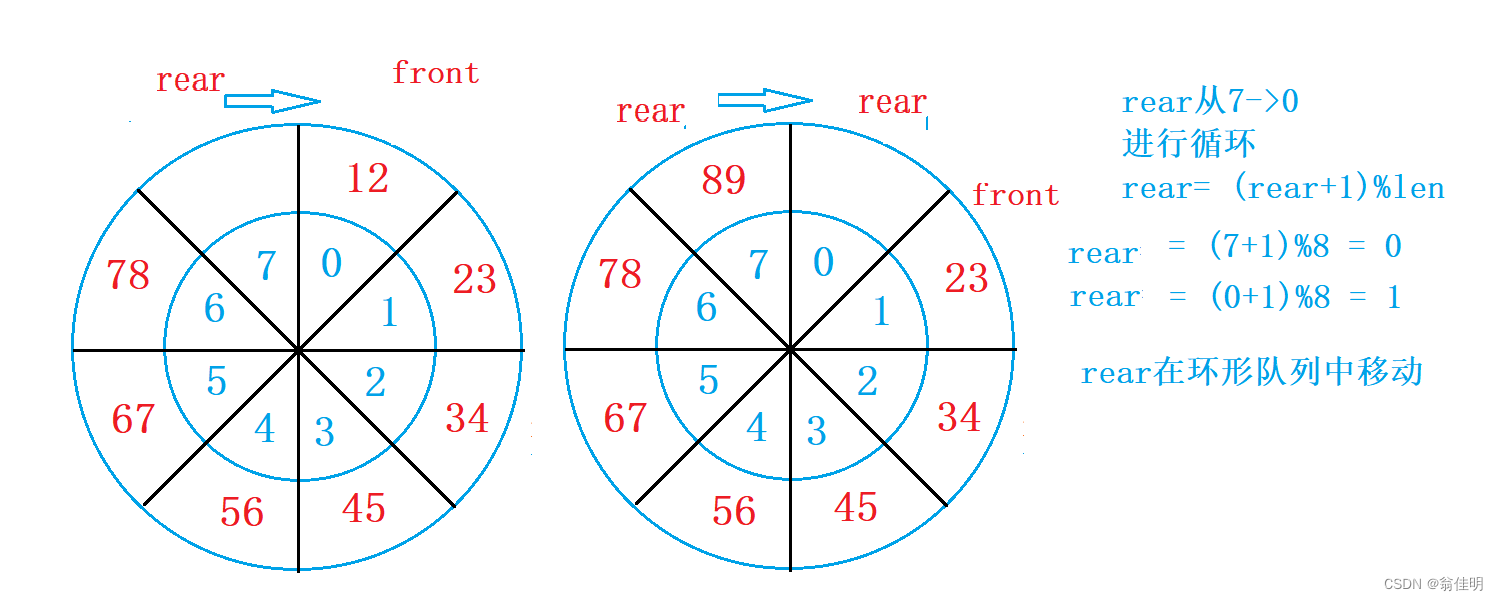
牺牲一个空间，当rear的下一个是front时，来判断数组是否满了
如果此时头结点是元素出队，将89入队，此时rear应该移动到0下标，
rear = （rear+1）%len :通过加一取余数组长度，完成数组索引的循环
当出队时，front从7下标移动到0小标：front = (front +1)%len

数组下标循环技巧
1.向后：下标 = （当前下标+要移动的距离）%数组长度
2.向前：小标 = （当前小标+数组长度-要移动的距离）%数组长度

4、双端队列(Deque)

双端队列：两端都能进出队列
deque 是 “double ended queue” 的简称

Deque是一个接口，使用时必须创建LinkedList对象
add和offer的区别：add在没有可用空间,无法插入元素时，会抛出一个异常

四、队列的使用

Queue是一个接口,它的底层是通过链表实现的
方法：offer入队、poll出队、peek获取队头、size个数、isEmpty判断队列是否为空

    public static void main(String[] args) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(1);//相当于尾插法
        queue.offer(2);
        queue.offer(3);
        queue.offer(4);
        System.out.println(queue.isEmpty());
        System.out.println(queue.size());
        queue.poll();
        System.out.println(queue.size());
        System.out.println(queue);
    }
    public static void main(String[] args) {
        Deque<Integer> deque = new LinkedList<>();双链表实现双端队列
        Queue<Integer> queue = new LinkedList<>();双链表实现普通队列
        LinkedList<Integer> stack = new LinkedList<>();  链式栈
        LinkedList<Integer> list = new LinkedList<>();当链表使用
        
        都是通过创建LinkedList对象实现，只不过实现了不同的接口
        Deque<Integer> deque1 = new ArrayDeque<>();底层由数组实现的双端队列
		 Deque<Integer> deque = new LinkedList<>();双链表实现双端队列
        
    	 Deque<Integer> stack1 = new ArrayDeque<>(); 双端队列实现顺序栈
		LinkedList<Integer> stack = new LinkedList<>();  双链表实现链式栈
    }

Queue是个接口，在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。
都是通过创建LinkedList对象实现，只不过实现了不同的接口
ArrayDeque,数组实现的双端队列

五、OJ题

1.设计循环队列

在这里插入图片描述

1.1 思路

1.环形队列底层通过数组实现，设置队头和队尾
2.因为要牺牲一个数组的空间，来判断是否队列满了，所以在生成数组时+1
3.判断数组是否为满：看rear的下一个是不是front
4.入队：如果队列满了，返回false,否则存进当前队尾下标，队尾通过公式以循环的方式移动一位
5.出队：队尾=队头，说明队列为空，不能出队，否则让队头通过公式以循环的方式移动一位

1.2 代码

class MyCircularQueue {

    private int[] elem;
    private int front;//队头
    private int rear;//队尾

    public MyCircularQueue(int k) {
        this.elem = new int[k+1];
    }

    //入队
    public boolean enQueue(int value) {
        //1.检查队列是否已满
        if (isFull()) {
            return false;
        } else {
            elem[rear] = value;
            rear = (1 + rear) % elem.length;
        }
        return true;
    }

    /**
     * 出队
     * @return
     */
    public boolean deQueue() {
        if (isEmpty()) {
            return false;
        } else {
            front = (front + 1) % elem.length;
        }
        return true;
    }

    public int Front() {
        if (isEmpty()){
            return -1;
        }
        return elem[front];

    }

    public int Rear() {//获取队尾元素，rear前一个下标
        if (isEmpty()){
            return -1;
        }
        int index =(rear == 0)?elem.length-1:rear-1;//判断0->7的情况
        return elem[index];
    }

    /**
     * 判断是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return rear == front;
    }

    /**
     * 判断队列是否为满
     *
     * @return
     */
    public boolean isFull() {
        //判断队尾的下一个是不是队头
        return (rear + 1) % elem.length == front;
    }
}

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue obj = new MyCircularQueue(k);
 * boolean param_1 = obj.enQueue(value);
 * boolean param_2 = obj.deQueue();
 * int param_3 = obj.Front();
 * int param_4 = obj.Rear();
 * boolean param_5 = obj.isEmpty();
 * boolean param_6 = obj.isFull();
 */

2.用队列实现栈

在这里插入图片描述

2.1 思路

栈是先进后出，队列是先进先出，一个队列无法实现，用两个队列实现
一个队列用来存储，一个队列为空
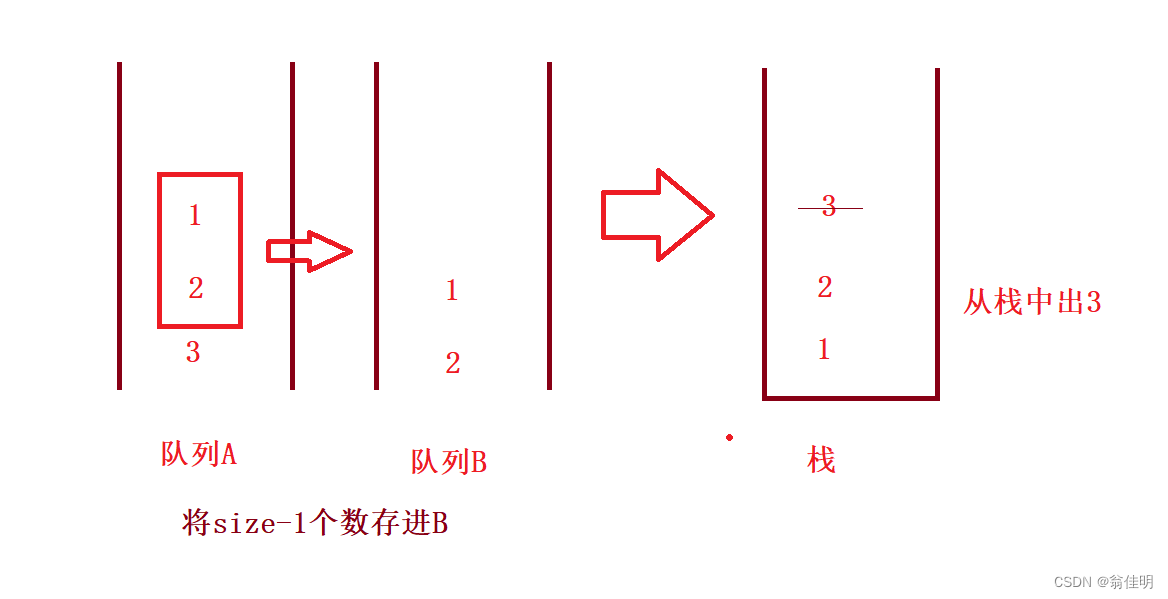
将size-1个数从不为空的队列取出，存到空队列中
原来队列中剩余的就相当于从栈中取出的，清空队列
存入的新队列的队尾，就相当于栈顶
如果继续从栈中出栈，再次size-1个数存进空队列
入栈：放进不为空的队列的队尾

2.2 图解

在这里插入图片描述

2.1 代码

class MyStack {
    private Queue<Integer> qu1;
    private Queue<Integer> qu2;

    public MyStack() {
        qu1 = new LinkedList<>();//初始化
        qu2 = new LinkedList<>();

    }

    public void push(int x) {
        if (!qu1.isEmpty()) {
            qu1.offer(x);

        } else if (!qu2.isEmpty()) {
            qu2.offer(x);
        } else {
            qu1.offer(x);
        }

    }

    public int pop() {
        int data = 0;
        if (empty()) {//两个队列都为空，当前栈为空，不能删元素
            return -1;
        }
        if (!qu1.isEmpty()) {
            int size = qu1.size();//size是不停变化的
            for (int i = 0; i < size - 1; i++) {
                int val = qu1.poll();
                qu2.offer(val);
            }
            return qu1.poll();//返回剩余的值
        } else {
            int size = qu2.size();
            for (int i = 0; i < size - 1; i++) {
                int val = qu2.poll();
                qu1.offer(val);
            }
            return qu2.poll();
        }
    }

    public int top() {
        if (empty()) {
            return -1;
        }
        if (!qu1.isEmpty()) {
            int val = -1;
            int size = qu1.size();
            for (int i = 0; i < size; i++) {
                val = qu1.poll();
                qu2.offer(val);
            }
            return val;
        } else {
            int val = -1;
            int size = qu2.size();
            for (int i = 0; i < size; i++) {
                val = qu2.poll();
                qu1.offer(val);
            }
            return val;
        }
    }

    public boolean empty() {
        return qu1.isEmpty() && qu2.isEmpty();
    }
}

3.用栈实现队列

在这里插入图片描述

3.1 思路

一个栈实现不了，需要用两个栈实现队列
入队：存进第一个栈中
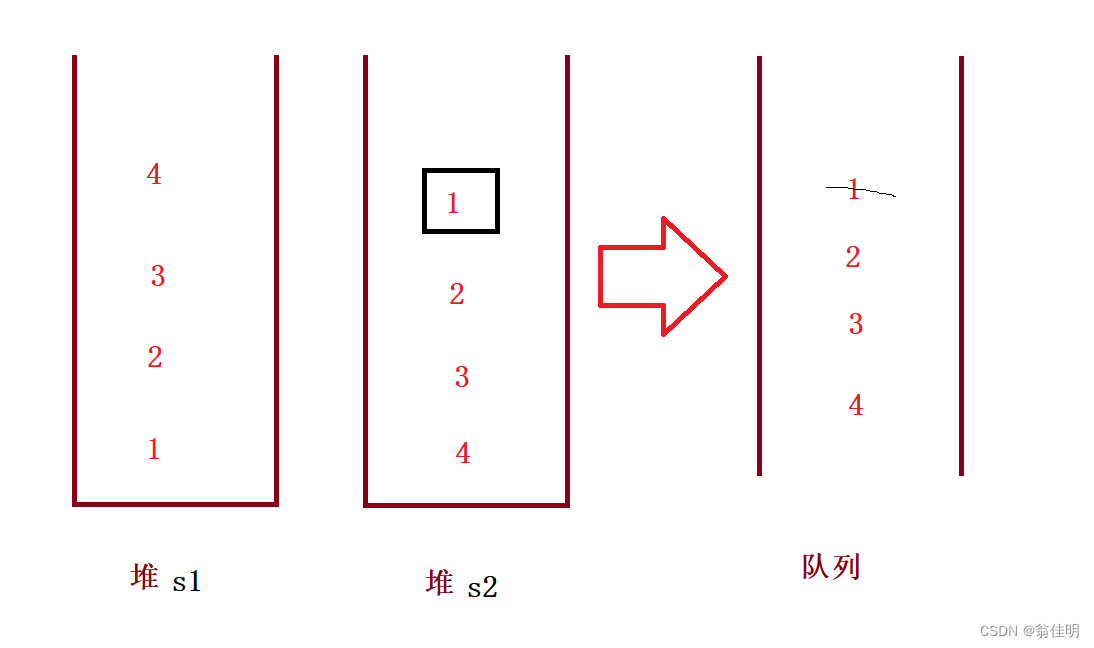
出队：如果第二个栈为空，将第一个栈的元素依次取出放进第二个栈，取出第二个栈的栈顶
如果第二个栈不为空，取出第二个栈的栈顶元素

3.2 图解

在这里插入图片描述

3.3 代码

class MyQueue2 {
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;

    public MyQueue2() {//初始化
        stack1 =new Stack<>();
        stack2 =new Stack<>();
    }

    public void push(int x) {
        stack1.push(x);//直接压入第一个栈
    }

    public int pop() {
        if (empty()){//判断两个栈是否都为空
            return -1;
        }
        int val = -1;
        if (stack2.isEmpty()){//第二个栈为空时，将第一个栈依次取出存进第二个栈
            int size = stack1.size();
            for (int i = 0; i < size; i++) {
               val = stack1.pop();
               stack2.push(val);
            }
        }
        val = stack2.pop();//取出第二个栈的栈顶
        return val;
    }

    public int peek() {//方法与pop一样，为简化写法、只是返回值不停
        if (empty()){
            return -1;
        }
        if (stack2.empty()){
            while (!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.peek();
    }

    public boolean empty() {//返回两个栈都为空的情况
        return stack2.isEmpty()&&stack1.isEmpty();
    }
}