37回溯算法-理论基础

news2025/11/1 7:57:42

什么是回溯算法

基本思想

问题场景

回溯算法的理解

回溯算法模板

LeetCode之路——257. 二叉树的所有路径

分析

什么是回溯算法

回溯算法是一种解决组合优化问题、搜索问题以及决策问题的算法。它通常用于尝试在一组可能的解决方案中搜索并找到满足特定条件的解。回溯算法通过逐步构建解决方案，如果在某一步无法继续前进，就会回溯到上一步，尝试其他选择，直到找到满足条件的解或搜索空间被完全探索。

基本思想

从初始状态开始，尝试选择一个可能的决策。
检查选择的决策是否符合问题的约束和条件。
如果符合，继续下一步；如果不符合，取消选择（回溯）。
重复步骤1和步骤2，直到找到解决方案或搜索空间被完全探索。

问题场景

组合问题：从一组元素中选择一个子集，使其满足特定条件。
排列问题：对一组元素进行排列，使其满足特定条件。
子集问题：找出一组元素的所有子集。
棋盘问题：在棋盘上寻找可行的路径或解决方案。
图论问题：在图中寻找路径或解决方案。

回溯算法通常是一种递归算法，其中递归函数用于处理每一步的决策和回溯。算法的关键部分是正确地实现选择和取消选择的逻辑，以确保在搜索空间中正确地前进和回退。

回溯算法的理解

理解回溯算法的关键是正确地实现选择和取消选择的逻辑，并理解问题的约束条件。

在解决复杂问题时，通常需要考虑优化策略，如剪枝、启发式搜索等，以提高算法的效率。回溯算法在解决许多实际问题中非常有用，因此它是一种重要的算法技巧。

回溯法解决的问题都可以抽象为树形结构，直白的说一棵高度有限的树（N叉树）。

回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯算法模板

建议诸君根据基本思想理解，这里简单举个例子：

// 1. 从初始状态开始，尝试选择一个可能的决策。
// 2. 检查选择的决策是否符合问题的约束和条件。
// 3. 如果符合，继续下一步；如果不符合，取消选择（回溯）。
// 4. 重复步骤1和步骤2，直到找到解决方案或搜索空间被完全探索。
void backtrack(参数) {
    // 找到解决方案或搜索空间被完全探索 = 终止条件
    if (终止条件) {
        存放结果;
        return;
    }
    
    // 从初始状态开始，尝试选择一个可能的决策。（回溯算法是一颗N叉树）
    for (决策 : 本次集合中元素) { // 节点的孩子数量就是集合的大小
        处理节点;
        backtrack(路径, 选择列表); //  符合，继续下一步
        回溯，撤销处理结果; // 不符合，取消选择（回溯）
    }
}

LeetCode之路——257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

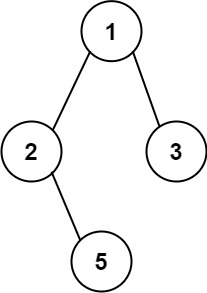
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

分析

1.终止条件：当前节点是叶子节点。

2.递归的条件：有子节点

非叶子节点：继续递归
叶子节点：追加路径

/**
 * 树节点定义
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> list = new ArrayList<String>();
        getPath(root, "", list);
        return list;
    }

    public void getPath(TreeNode node, String path, List<String> list) {
        if (node != null) {
            path += node.val;
            // 叶子节点，追加路径
            if (node.left == null && node.right == null) {
                list.add(path);
            } else {
                path += "->";
                getPath(node.left, path, list);
                getPath(node.right, path, list);
            }
        }
    }
}