TLSF——一种高效的内存池实现

news2024/11/28 9:31:39

起源于计算内核关于堆内存使用的相关优化。
系统调用分配和回收内存的开销较大，一个优化是预先通过系统调用分配一大块内存，然后每次内存使用从大块内存中切出一小份内存使用。
Arena用于维护大块内存切分出来的大量小块内存，达到高效分配和释放内存的效果。

C++的malloc API封装了Arena逻辑和内存分配系统调用。
Arena的本来含义是“竞技场”，在有的地方直接翻译为“内存池”。

Velox使用了TLSF Arena。
在这里插入图片描述
所以Arena算法都需要回答两个问题：

Sequential Fit：将FreeBlock根据大小从小到大排列。分配内存时，从小到大遍历，直到找到满足要求的最小FreeBlock。
Segragated Free Lists：分成多个FreeBlock链。每一条链维护特定大小（或者特定大小范围）的FreeBlock。分配内存时，先找到对应的链条，然后再从链条中找到合适的Block。
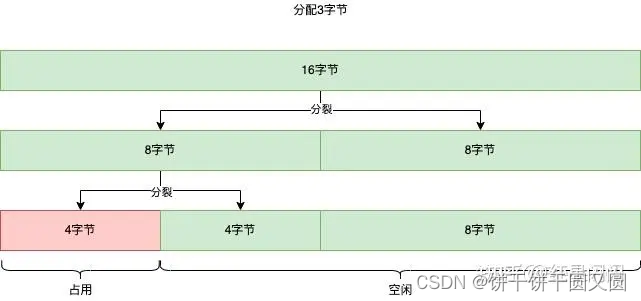
Buddy Systems。
Indexed Fist：FreeBlock的size为Key，FreeBlock的地址为Value，使用index（比如平衡树）维护Key。

时间复杂度对比

Sequential Fit：O(N)顺序遍历，N是FreeBlock的个数。
Segregated Free Lists：将其视为Sequential Fit的改进，每一个槽位不是一个Block，而是大小相同（或在一定范围内）的Block链条。当BlockSize类别较少，线性分割内存大小区间，直接根据BlockSize定位到对应的槽位：O(1)。当BlockSize类别较多，指数分割内存大小区间：O(1)时间定为槽位，顺序遍历槽位内的内存块大小O(M)。M为每个Block链的平均长度。
Buddy Systems：O(log N)
IndexedFit：O(log N)和索引相关，以平衡二叉树为例。

要解决的问题
TLSF（Two-Level Sergregated Fit）Arena的内存碎片较小，且分配释放时间复杂度都是O(1)。复杂度都是O(1)意味着TLSF可以运用于实时系统，因为其内存分配和释放耗时是有边界的。

数据结构
所有的内存块都被同时维护在两个链表中：

Segregated list：主要用于分配指定大小的BlockSize，仅维护FreeBlock。
Physical list：主要用于内存块的合并，维护所有Block，包括FreeBlock和分配出去的Block，所有的Block根据内存的物理地址顺次连接。

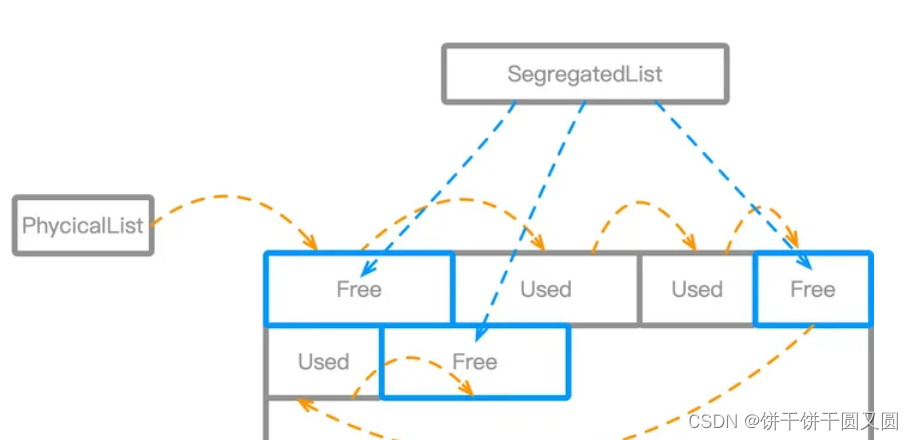
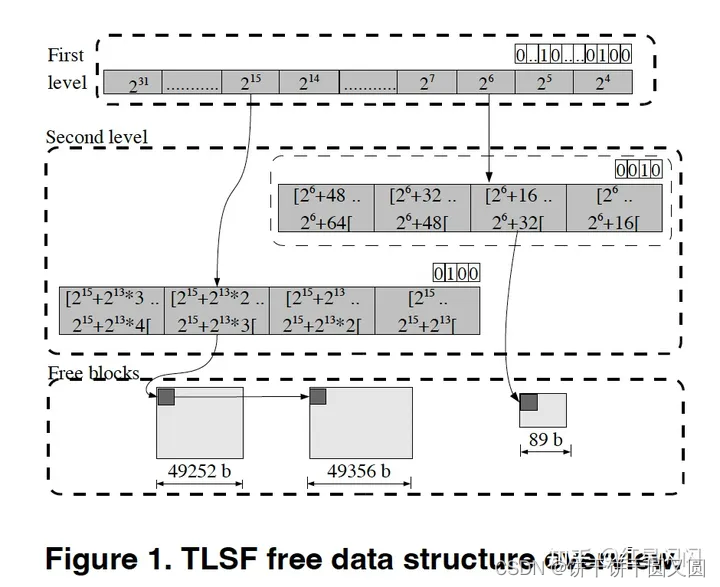
在这里插入图片描述

Segegated list分成两个level：

First Level：是一个数组，存储指向SecondLevel的指针，数组槽位表示BlockSize的量级，从右往左分别是2⁴、2⁵、…。
Second Level：是一个数组，数组槽位表示FirstLevel指定的内存大小的线性分割。槽位个数为divison，由Config配置的SLI（Second Level Index）决定。SLI为2，则Division为2²=4，表示将内存现象分割为4份。槽位中存储指向对应大小的FreeBlock链表地址。
FirstLevel和SecondLevel右上角表示对应的BitMap，表示对应槽位是否有FreeBlock

举例

需要分配一块85B的内存块，首先判断其内存大小属于哪一个量级，⌊log(85)⌋ = 6。
然后查询FirstLevel，找到2⁶的槽位，2⁶槽位表示[2⁶~2⁷)的内存块都在这个槽位里找。
通过2⁶槽位进而找到对应的SecondLevel，SecondLevel将大小区间划分为4份，分为为[2^6 + 0, 2^6 + 16), [2^6 + 16, 2^6 + 32), [2^6 + 32, 2^6 + 48), [2^6 + 48, 2^6 + 64)。
85=2⁶+21落在第二个区间，于是从SecondLevel第二个槽位进入，找到对应的FreeBlock。
FreeBlock对应的大小为89Byte，多出4Byte，由于FreeBlock大小至少为2⁴，所以直接分配89Byte的内存块，4Byte为内部碎片。

BlockHeader主要字段

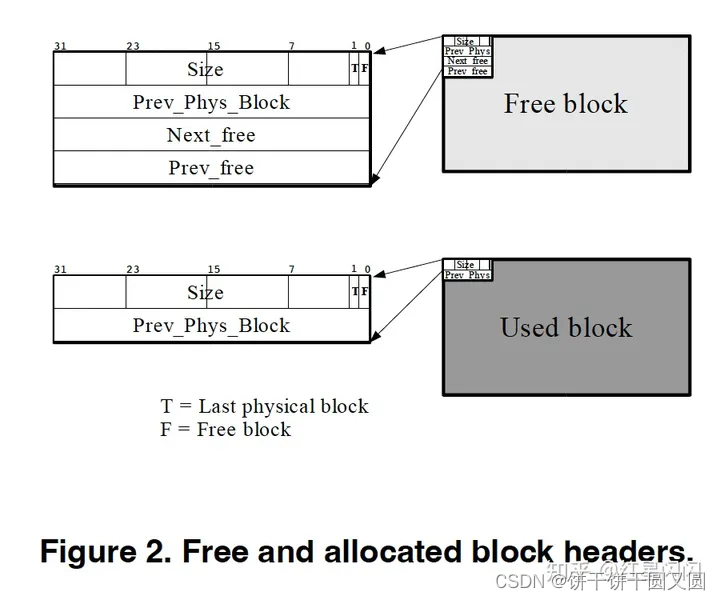
在这里插入图片描述

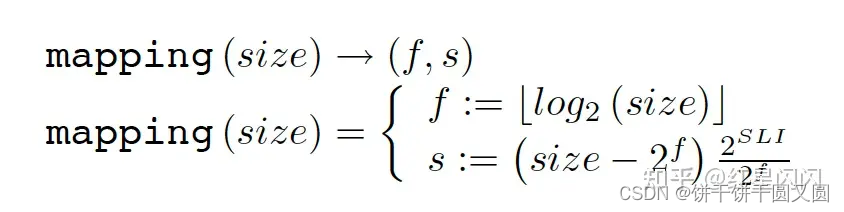
在这里插入图片描述
如函数mapping，给点一个内存块大小，可以快速定位对应的FreeBlock所在的FirstLevel偏移f，和Second Level偏移S。

f：如前文所述，f决定的是内存大小的量级，可以直接通过log计算得到。
s：s决定的是内存大小量级内线性分割的偏移，（size-2^f）是超出对应两级最小值的大小。SecondLevel将[2^f,2^f+1)的内存区间等分成2^SLI份，所以该公式是对应大小所在的槽位。

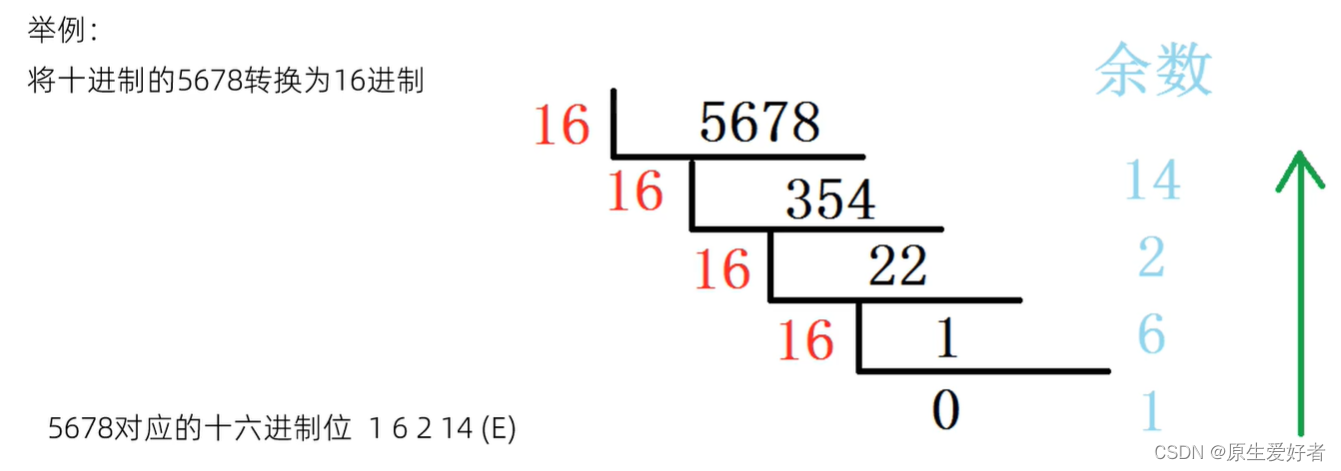
具体到代码实现，log计算就是对应值的二进制表示的最左边1所在位数，比如十进制数460，最左边的1在第8位，其大小量级就是2⁸，就是FirstLevel的偏移f为8。后面紧跟SLI位数字表示SeconfLevel的偏移s，下图是1100，也就是12。

通过简单计算就可以定位到对应大小的FreeBlock，时间复杂度为O（1）。

其实TLSF是对Segregated Free List的改进。Segregated Free List有两种：

如果线性分割，则O（1）的时间复杂度就可以找对应的FreeBlock，但是需要维护的槽位过多，设想线性分割的Segregated Free Lists，最大内存块为1G，碎片Fragment限定到16Byte内，则需要划分1G/16=2^26个槽位。
如果指数分割，可以大大减少槽位个数，同样是最大内存块为1G，碎片Fragment限定到16Byte内，只需要log(1G)=30个槽位，但是每一个槽位里内存大小值域变化较大，找到合适的FreeBlock需要顺序遍历，时间复杂度为O(M)，M为每一个槽位里的平均FreeBlock个数。

所有，当内存大小较小，线性分割的Segregated Free Lists的效果更好（槽位个数在可接受范围内，时间复杂度为O（1）），当内存大小区间较大，指数分割的Segregated Free Lists的效果更好（主要为了槽位数在可控范围内。）

一个自然优化思路就是将线性分割和指数分割结合起来，这样既可以减少槽位个数，又可以快速定位槽位。
TLSF就是这样做，FirstLevel用于指数分割，尽可能减少了槽位数，Second用于线性分割，可以快速定位FreeBlock。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1145993.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！