在当今数据驱动的世界中,计算平面点集的最小外接轮廓面积被广泛应用于各种实际场景中。它是一项重要而魅力十足的任务,旨在找到一个最小的矩形或多边形区域,能够完全包围给定的离散点集。这个看似简单的问题背后隐藏着许多挑战,需要结合数学、计算几何和优化方法来解决。
计算平面点集的最小外接轮廓面积对很多领域具有重大意义。首先,在计算机视觉中,它是目标检测和图像分割等任务的关键步骤。通过确定目标物体的最小外接轮廓面积,我们可以更好地理解和描述物体的形状,从而实现更准确的目标识别和跟踪。在自动驾驶系统中,该技术可用于检测道路边缘或障碍物边界,从而帮助车辆规划路径并做出决策。此外,在工业制造、地理信息系统和城市规划等领域,计算点集的最小外接轮廓面积可以提供宝贵的空间分析和形状建模工具。
在过去的几十年里,研究者们积极探索计算平面点集最小外接轮廓面积的求解方法,并取得了重要的进展。早期的方法主要基于几何学原理,如旋转卡壳、凸包和分治策略等。这些传统的方法虽然在某些场景下表现良好,但对于复杂点集和大规模数据的处理存在一定限制。近年来,随着计算机性能的提升和数值优化算法的发展,一些新颖且高效的方法应运而生。
最近的研究工作集中在提高算法的效率和鲁棒性。基于机器学习的方法,如支持向量机(SVM)和人工神经网络,被引入以改善凸包计算的精度和速度。此外,通过多核处理、并行计算和GPU加速等技术,研究人员努力提高算法的运行效率,使其能够处理更大规模的点云数据。同时,深度学习技术的发展也为计算平面点集最小外接轮廓面积带来了新的可能性,例如使用卷积神经网络进行分割和轮廓估计。
值得一提的是,随着三维扫描技术的广泛应用,研究者们开始将计算平面点集最小外接轮廓面积推广到三维点云数据,并发展了一系列新的算法。这些算法旨在从复杂的三维场景中提取最小外接体积或曲面,具有很高的实用价值。
总结而言,计算平面点集最小外接轮廓面积是计算机视觉、图像处理和模式识别等领域中一个关键且挑战性的任务。通过求解这个问题,我们可以从离散的点集中提取出有价值的形状信息,为目标检测、自动驾驶和空间建模等应用提供强大的支持。随着技术的不断进步与创新,我们可以期待在这个领域看到更多令人激动的发展和突破。
下面介绍两个案例:
1、先计算凸包,再计算面积
凸包法是一种常用的方法来计算平面点集的最小外接轮廓面积。它基于数学几何原理,通过找到形成凸包的点集来估计最小外接轮廓面积。以下是凸包法的优点和缺点:
优点:
简单直观:凸包法的基本原理易于理解。它可以通过简洁的步骤将点集收束为一个多边形或凸多边形,容易在可视化和概念上表示。
准确性:当点集满足凸性时,凸包法能够提供精确的最小外接轮廓面积。这使得凸包法在许多实际情况下产生可靠的结果。
快速计算:相比其他复杂的算法,凸包法具有很高的计算效率。在点集规模较小时,凸包法通常能够在很短的时间内计算出最小外接轮廓面积。
适用广泛:凸包法适用于各种不同类型的点集,不论其分布是否均匀、是否存在噪声点等。因此,凸包法具有广泛的适用性,并且可以用于多个领域中的问题求解。
缺点:
复杂形状限制:凸包法在处理具有复杂形状的点集时可能存在局限性。由于凸包要求生成一个完全包围点集的凸多边形,因此对于非凸点集或存在内部空洞的点集,凸包法无法提供准确和合理的结果。
对噪声点敏感:凸包法对噪声点较为敏感。当点集中存在离群点或噪声点时,这些点可能会影响最终的凸包结果,导致外接轮廓面积计算不准确。
计算效率随规模增加:虽然凸包法在小规模点集上运行速度较快,但随着点集规模的增加,其计算效率可能迅速下降。对于大规模点集,凸包法的计算时间可能变得相当昂贵。
实现复杂性:尽管凸包法的基本原理简单易懂,但实现优化的凸包算法可能需要复杂的编程技巧和数据结构支持。这使得实施和调试凸包算法可能具有一定的挑战性。
综上所述,凸包法作为计算平面点集最小外接轮廓面积的一种常见方法,具有诸多优点。它简单直观、计算快速,并适用于各种情况。然而,它在处理复杂形状和存在噪声点的点集时可能存在一些局限性。因此,在实际应用中,我们需要根据问题的特点选择合适的方法或结合其他技术来解决具体的求解任务。
import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
# 指定字体文件路径
import matplotlib.font_manager as fm
font_path = 'C:/Windows/Fonts/simhei.ttf'
prop = fm.FontProperties(fname=font_path)
# 定义椭圆上的点作为示例点集
points = np.array([[1, 0], [0.866, 0.5], [0.5, 0.866], [0, 1], [-0.5, 0.866], [-0.866, 0.5],
[-1, 0], [-0.866, -0.5], [-0.5, -0.866], [0, -1], [0.5, -0.866], [0.866, -0.5]])
# 计算点集的凸包
hull = ConvexHull(points)
# 获取凸包的顶点坐标
vertices = hull.points[hull.vertices]
# 绘制凸包边界和点集
plt.plot(points[:,0], points[:,1], 'o', label='点集')
plt.plot(vertices[:,0], vertices[:,1], 'r--', lw=2, label='凸包边界')
plt.xlabel('x', fontproperties=prop)
plt.ylabel('y', fontproperties=prop)
plt.title('凸包与点集', fontproperties=prop)
plt.legend(prop=prop)
plt.grid(True)
plt.axis('equal')
plt.show()
# 计算凸包顶点形成的多边形的面积
area = hull.area
print("凸包顶点坐标:\n", vertices)
print("凸包面积大小:", area)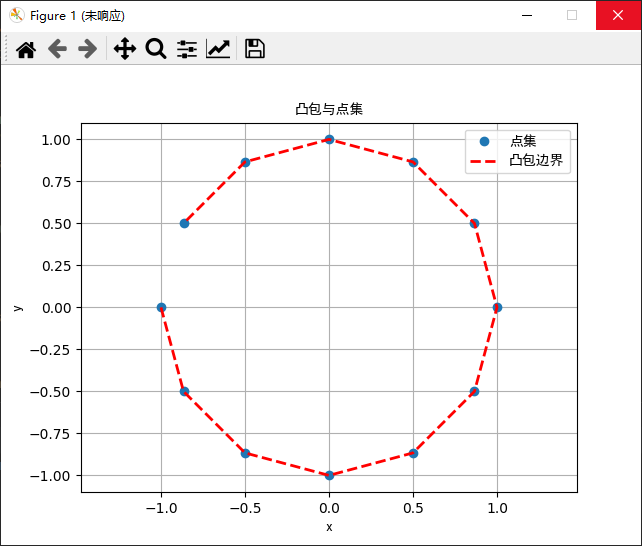
凸包顶点坐标:
[[-1. 0. ]
[-0.866 -0.5 ]
[-0.5 -0.866]
[ 0. -1. ]
[ 0.5 -0.866]
[ 0.866 -0.5 ]
[ 1. 0. ]
[ 0.866 0.5 ]
[ 0.5 0.866]
[ 0. 1. ]
[-0.5 0.866]
[-0.866 0.5 ]]
凸包面积大小:6.211565981473167(理论面积为np.pi)
注意:面积还有一定差距,可以取多一些点数,减小误差
2、把平面点集轮廓映射到图像中,通过opencv函数cv2.contourArea计算面积
这种方法也适用于内凹的点集,解决凸包法不能完成的任务。
import matplotlib.pyplot as plt
import cv2
import numpy as np
# 圆弧参数
radius = 1.0
start_angle = 0 # 起始角度,单位:度
end_angle = 270 # 终止角度,单位:度
num_points_arc = 1000 # 圆弧上的数据点个数
# 起始角度和终止角度转换为弧度
start_angle_rad = np.deg2rad(start_angle)
end_angle_rad = np.deg2rad(end_angle)
# 计算圆弧上点的极坐标
theta_arc = np.linspace(start_angle_rad, end_angle_rad, num=num_points_arc)
x_arc = 0+radius * np.cos(theta_arc)
y_arc = 0+radius * np.sin(theta_arc)
# 直线参数
line1_start_point = (0, 0)
line1_angle = start_angle_rad
line2_start_point = (0,0)
line2_angle = end_angle_rad
# 计算直线上的数据点
num_points_line = 1000 # 每条直线上的数据点个数
l=np.linspace(0, radius, num=num_points_line)
x_line1 = line1_start_point[0]+l*np.cos(line1_angle)
y_line1 = line1_start_point[1]+l*np.sin(line1_angle)
x_line2 = line2_start_point[0]+l*np.cos(line2_angle)
y_line2 = line2_start_point[1]+l*np.sin(line2_angle)
# 将数据点合并
X = [x_line1,x_arc,x_line2[::-1]]
Y = [y_line1,y_arc,y_line2[::-1]]
fig = plt.figure(figsize=(5, 5))
plt.rcParams['xtick.direction'] = 'in' # 将x周的刻度线方向设置向内
plt.rcParams['ytick.direction'] = 'in' # 将y轴的刻度方向设置向内
clist = ['blue', 'red', 'green', 'black', 'darkgreen', 'lime', 'gold', 'purple', 'green', 'cyan', 'salmon', 'grey',
'mediumvioletred', 'darkkhaki', 'gray', 'darkcyan', 'violet', 'powderblue']
# for i in range(len(X)):
# plt.plot(X[i],Y[i], c=clist[i%17])
# plt.tight_layout()
# plt.show()
# 创建空白图像
blank_image = np.zeros((1400, 1400), dtype=np.uint8)
#坐标变换
X_new=np.array(X).flatten()+radius
Y_new=-1*np.array(Y).flatten()+radius
# 转换为整型数组
X_shifted = np.array(X_new*700, dtype=np.int32)
Y_shifted = np.array(Y_new*700, dtype=np.int32)
# 绘制轮廓
points = np.column_stack((X_shifted, Y_shifted))
cv2.drawContours(blank_image, [points], contourIdx=0, color=255, thickness=3)
# 计算轮廓围成的面积
area = cv2.contourArea(points)/700/700
# 理论面积计算
theta_span = end_angle_rad - start_angle_rad
theoretical_area = 0.5 * radius * radius * theta_span
# 输出面积结果并与理论面积对比
print("轮廓围成的面积:", area)
print("理论面积:", theoretical_area)
print("面积差值:", area - theoretical_area)
# 显示图像
cv2.namedWindow('Contour Image',0)
cv2.imshow("Contour Image", blank_image)
cv2.waitKey(0)
cv2.destroyAllWindows()轮廓围成的面积:2.3565163265306124
理论面积:2.356194490192345
面积差值:0.0003218363382675449



![[动态规划] (二) LeetCode 面试题 08.01.三步问题](https://img-blog.csdnimg.cn/img_convert/25bf52d2f096a8590b1038e9f88d7439.png)

![NSS [鹤城杯 2021]EasyP](https://img-blog.csdnimg.cn/img_convert/9b91a65ed72d5c1f215c694ab99b27c1.png)