下面结合代码和原理进行深入分析Transformer原理。

2 Transformer深入分析

对于CV初学者来说，其实只需要理解Q K V 的含义和注意力机制的三个计算步骤：

1. Q 和所有 K 计算相似性；
2. 对相似性采用 Softmax 转化为概率分布；
3. 将概率分布和 V 进行一 一对应相乘，最后相加得到新的和 Q 一样长的向量输出即可。

重点是下面要讲的Transformer结构

下面按照 编码器输入数据处理 -> 编码器运行 -> 解码器输入数据处理 -> 解码器运行 -> 分类head 的实际运行流程进行讲解。

2.1 编码器输入数据处理

2.1.1 源单词嵌入

以翻译任务为例，原始待翻译输入是三个单词：

输入是三个单词，为了能够将文本内容输入到网络中，肯定需要进行向量化（不然单词如何计算？），
具体是采用NLP领域的Embedding算法进行词嵌入，也就是常说的Word2Vec。
对于CV来说知道是干嘛的就行，不必了解细节。
假设每个单词都可以嵌入成512个长度的向量，故此时输入即为3x512，注意Word2Vec操作只会输入到第一个编码器中，后面的编码器接收的输入是前一个编码器输出。

为了便于组成batch(不同训练句子单词个数肯定不一样)进行训练，可以简单统计所有训练句子的单词个数，取最大即可，假设统计后发现待翻译句子最长是10个单词，那么编码器输入是10x512，额外填充的512维向量可以采用固定的标志编码得到，例如$$。

2.1.2 位置编码 Positional Encoding

采用经过单词嵌入后的向量输入到编码器中还不够，因为Transformer内部没有类似RNN的循环结构，没有捕捉顺序序列的能力，
或者说无论句子结构怎么打乱，Transformer都会得到类似的结果。
为了解决这个问题，在编码词向量时会额外引入了位置编码Position Encoding向量表示两个单词 i 和 j 之间的距离，简单来说就是在词向量中加入了单词的位置信息。

加入位置信息的方式非常多，最简单的可以是直接将绝对坐标0,1,2编码成512个长度向量即可。
作者实际上提出了两种方式：

• 网络自动学习
• 自己定义规则

提前假设单词嵌入并且组成batch后，shape为(b,N,512)，N是序列最大长度，512是每个单词的嵌入向量长度，b是batch

（1） 网络自动学习

self.pos_embedding = nn.Parameter(torch.randn(1, N, 512))

torch.nn.Parameter是继承自torch.Tensor的子类，其主要作用是作为nn.Module中的可训练参数使用。
torch.randn函数用于生成正态分布随机数的张量。

比较简单，因为位置编码向量需要和输入嵌入(b,N,512)相加，所以其shape为(1,N,512)表示N个位置，每个位置采用512长度向量进行编码

（2） 自己定义规则

自定义规则做法非常多，论文中采用的是sin-cos规则，具体做法是：

1. 将向量(N,512)采用如下函数进行处理

$$P{E}_{(pos,2i)}=\text{sin}(\frac{pos}{10000^{2i/d_{model}}})$$

$$P{E}_{(pos,2i+1)}=\text{cos}(\frac{pos}{10000^{2i/d_{model}}})$$
pos即0~N，i是0-511

2. 将向量的512维度切分为奇数行和偶数行
3. 偶数行采用sin函数编码，奇数行采用cos函数编码
4. 最后按照原始行号拼接

实现代码如下：

def get_position_angle_vec(position):
    # d_hid是0-511,position表示单词位置0～N-1
    return [position / np.power(10000, 2 * (hid_j // 2) / d_hid) for hid_j in range(d_hid)]

# 每个单词位置0～N-1都可以编码得到512长度的向量
sinusoid_table = np.array([get_position_angle_vec(pos_i) for pos_i in range(n_position)])
# 偶数列进行sin
sinusoid_table[:, 0::2] = np.sin(sinusoid_table[:, 0::2])  # dim 2i
# 奇数列进行cos
sinusoid_table[:, 1::2] = np.cos(sinusoid_table[:, 1::2])  # dim 2i+1

np.power()用于数组元素求n次方。 hid_ j // 2的目标是输入是 2i 或者 2i+1

上面例子的可视化如下：

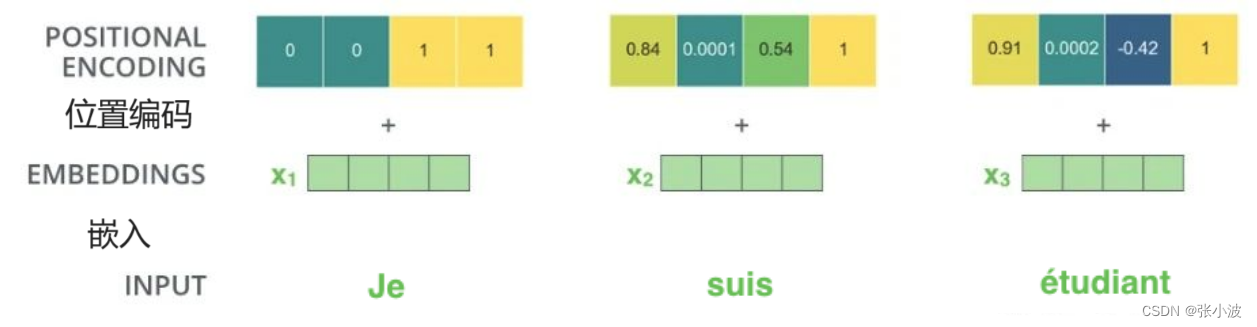
如此编码的优点是能够扩展到未知的序列长度，例如，前向时候有特别长的句子，其可视化如下：（位置 -1到1，sin和cos最小值到最大值）

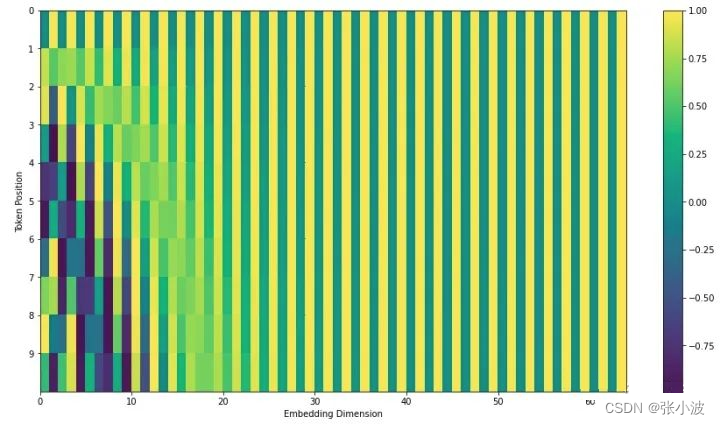
作者为啥要设计如此复杂的编码规则？
原因是sin和cos的如下特性：
$$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$

$$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$

可以将PE(pos+k)用PE(pos)进行线性表出：

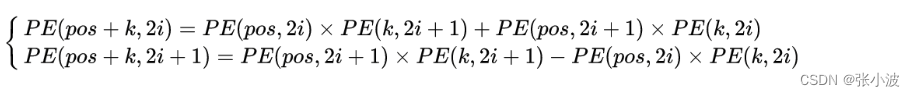
假设k=1，那么下一个位置的编码向量可以由前面的编码向量线性表示，等价于以一种非常容易学会的方式告诉了网络单词之间的绝对位置，让模型能够轻松学习到相对位置信息。
注意编码方式不是唯一的，将单词嵌入向量和位置编码向量相加就可以得到编码器的真正输入了，其输出shape是(b,N,512)。

2.2 编码器前向过程

编码器由两部分组成：自注意力层和前馈神经网络层。

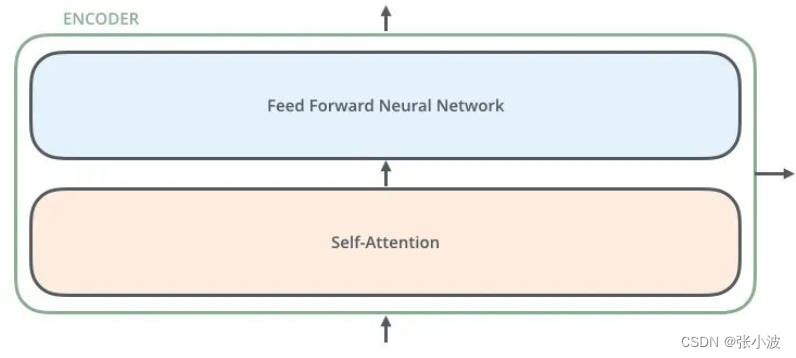
其前向可视化如下：

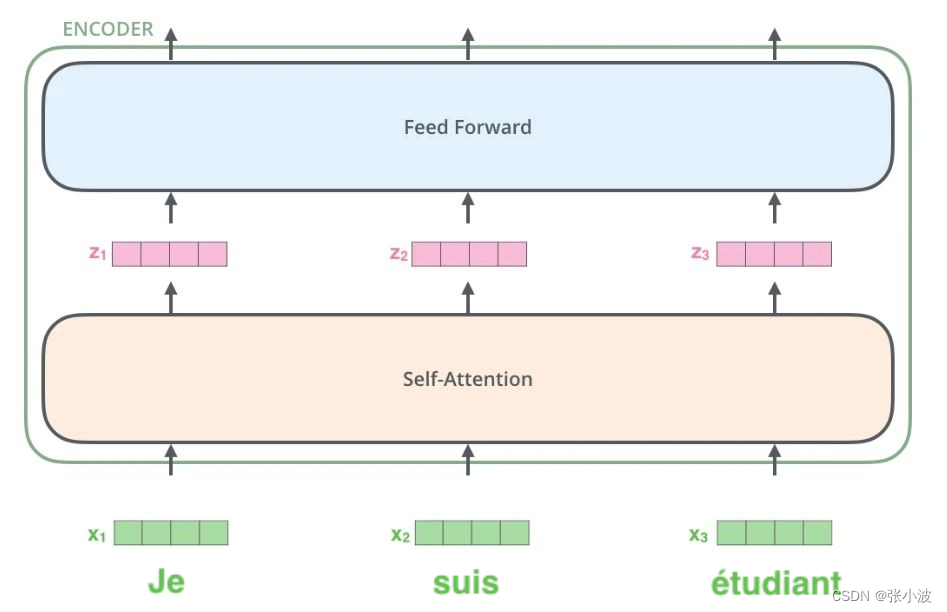
注意上图没有绘制出单词嵌入向量和位置编码向量相加过程，但是是存在的。

2.2.1 自注意力层

通过前面分析我们知道自注意力层其实就是Attention操作，并且由于其QKV来自同一个输入，故称为自注意力层。
在参考资料1博客里面举了个简单例子来说明Attention的作用：

假设我们想要翻译的输入句子为
The animal didn’t cross the street because it was too tired，
这个 “it” 在这个句子是指什么呢？它指的是street还是这个animal呢？这对于人类来说是一个简单的问题，但是对于算法则不是。
当模型处理这个单词 “it” 的时候，自注意力机制会允许 “it” 与 “animal” 建立联系，即随着模型处理输入序列的每个单词，自注意力会关注整个输入序列的所有单词，帮助模型对本单词更好地进行编码。
实际上训练完成后确实如此，Google提供了可视化工具，如下所示：

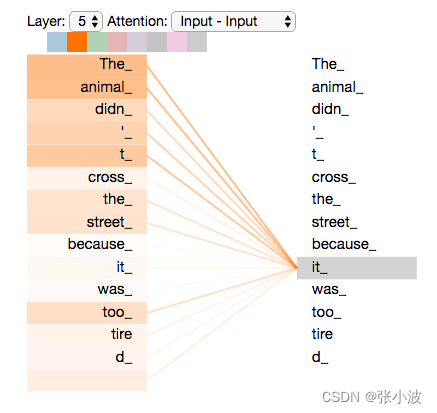
上述是从宏观角度思考，如果从输入输出流角度思考，也比较容易：

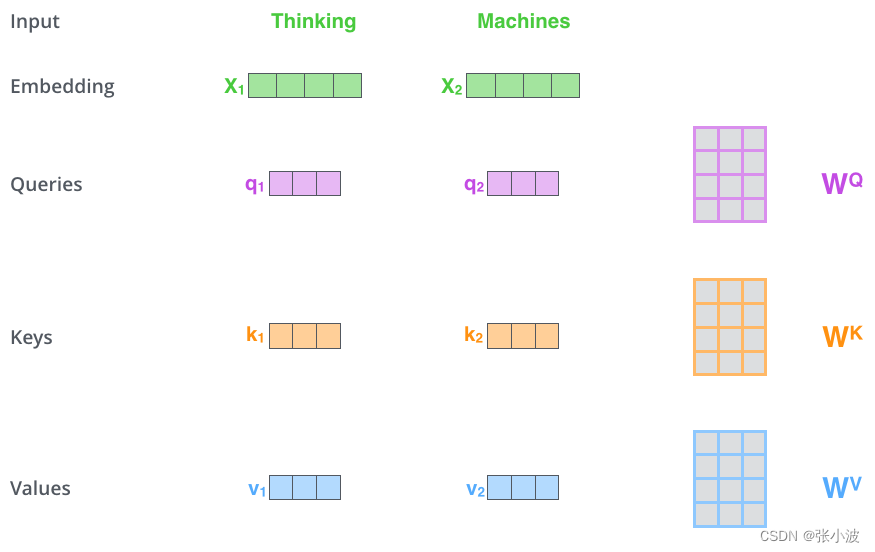
假设我们现在要翻译上述两个单词，
首先，将单词进行编码，和位置编码向量相加，得到自注意力层输入 X , 其shape为(b,N,512)；
然后，定义三个可学习矩阵 WQ、WK、WV (通过nn.Linear 全连接层实现)，其shape为(512,M)，一般M等于前面维度512，从而计算后维度不变；
接着，将X和矩阵WQ、WK、WV 相乘，得到 Q K V 输出，shape为(b,N,M)；

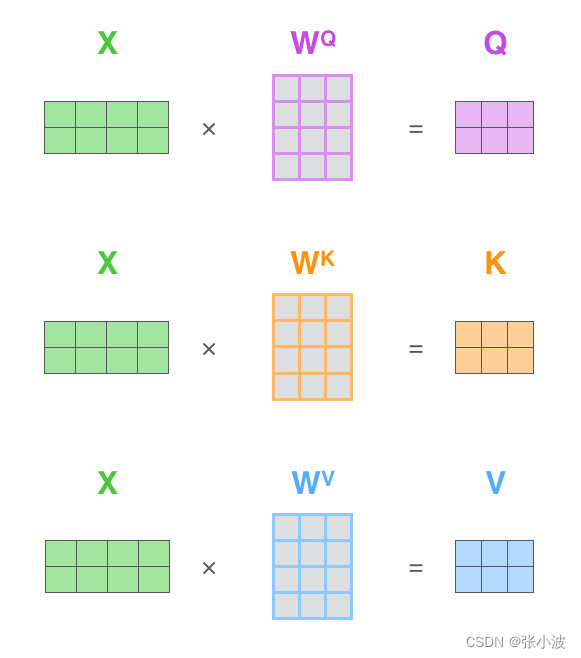
再者，将 Q 和 K 进行点乘计算向量相似性；采用 softmax 转换为概率分布；将概率分布和V进行加权求和即可。
其可视化如下：

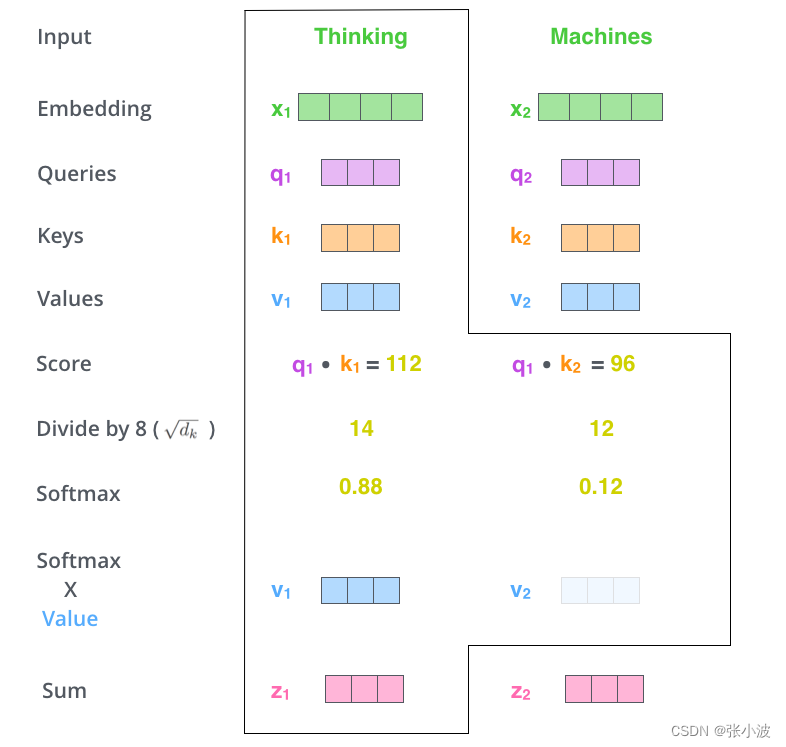
上述绘制的方框不是矩阵形式，更好理解而已。
对于第一个单词的编码过程是：
将 q1 和所有的 k 进行相似性计算，然后除以维度的平方根(论文中是 64，本文可以认为是512) 使得梯度更加稳定，然后通过Softmax传递结果，这个Softmax分数决定了每个单词对编码当下位置(“Thinking”)的贡献，最后对加权值向量求和得到z1。

这个计算很明显就是前面说的注意力机制计算过程，每个输入单词的编码输出都会通过注意力机制引入其余单词的编码信息。

上述为了方便理解才拆分这么细致，实际上代码层面采用矩阵实现非常简单：

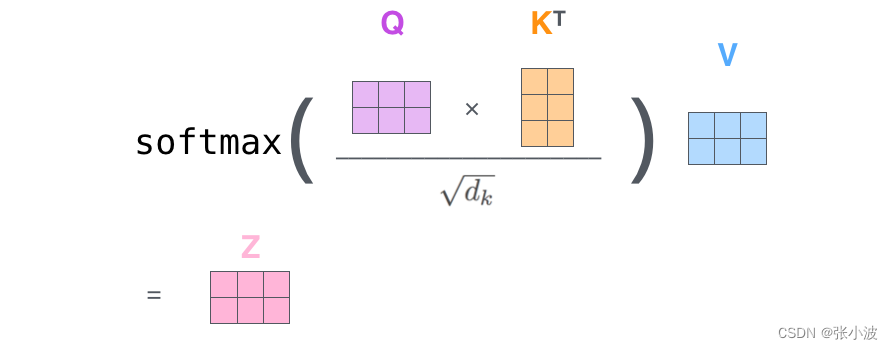
上面的操作很不错，但是还有改进空间，论文中又增加一种叫做“多头”注意力（“multi-headed” attention）的机制进一步完善了自注意力层，并在两方面提高了注意力层的性能：

• 它扩展了模型专注于不同位置的能力。在上面的例子中，虽然每个编码都在z1中有或多或少的体现，但是它可能被实际的单词本身所支配。如果我们翻译一个句子，比如 “ The animal didn’t cross the street because it was too tired”，我们会想知道“it ” 指的是哪个词，这时模型的 “多头” 注意机制会起到作用。
• 它给出了注意力层的多个 “表示子空间"，对于“多头” 注意机制，有多个Q查询/K键/V值权重矩阵集(Transformer使用8个注意力头，因此我们对于每个编码器/解码器有8个矩阵集合)。

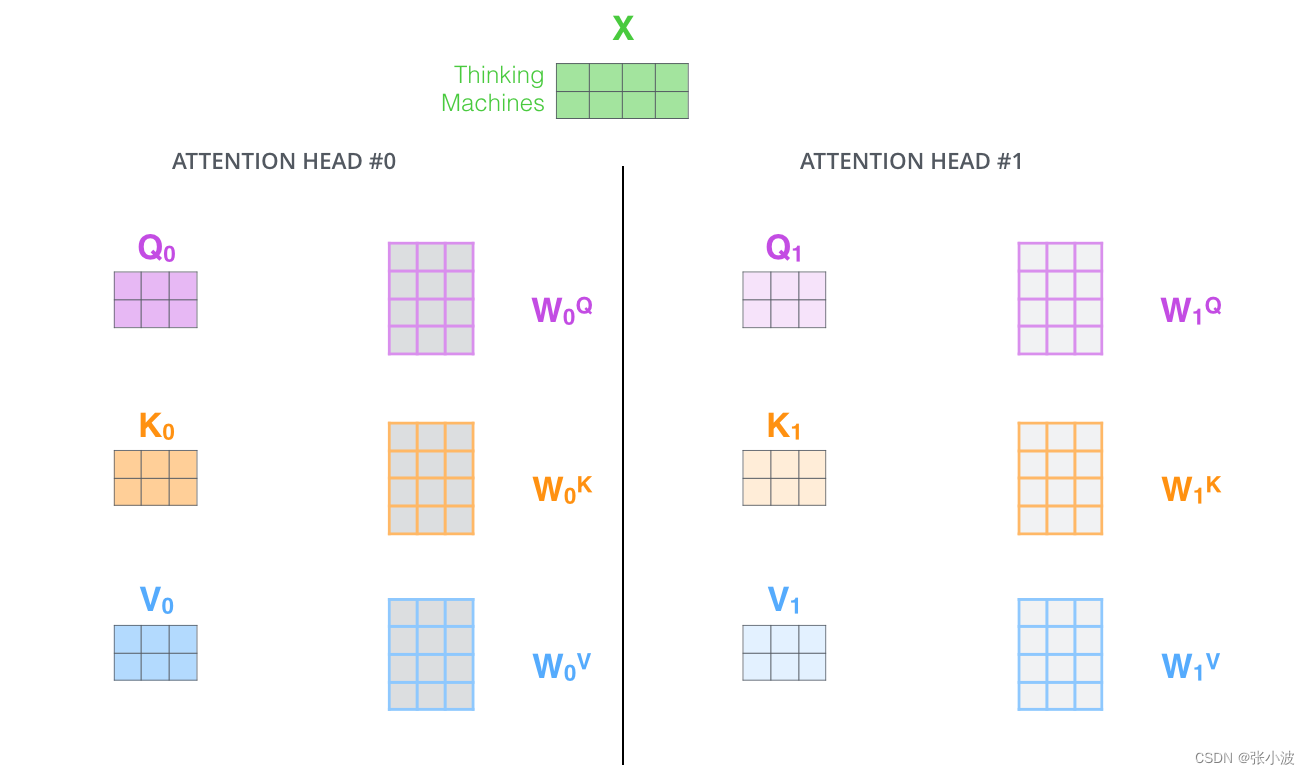
简单来说就是类似于分组操作，将输入 X 分别输入到8个attention层中，得到8个Z矩阵输出，最后对结果Concat即可。
论文图示如下：

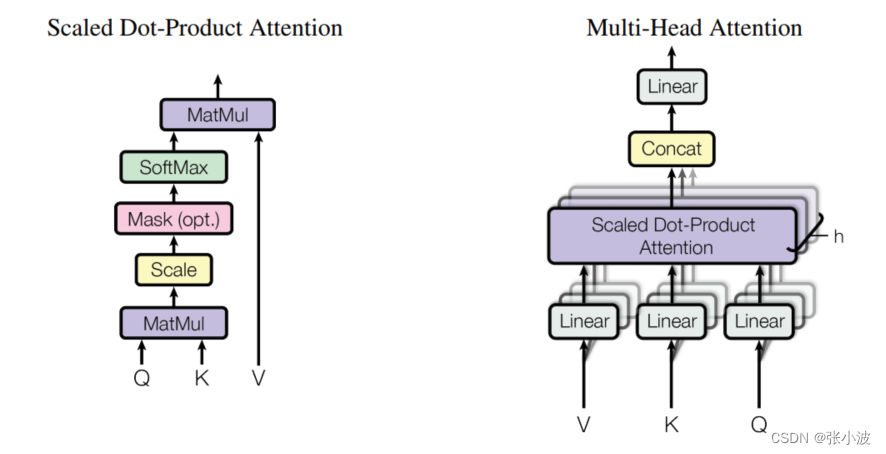
先忽略Mask的作用，左边是单头attention操作，右边是n个单头attention构成的多头自注意力层。
代码层面非常简单，单头attention操作如下：

class ScaledDotProductAttention(nn.Module):
    ''' Scaled Dot-Product Attention 缩放点积注意力'''

    def __init__(self, temperature, attn_dropout=0.1):
        super().__init__()
        self.temperature = temperature
        self.dropout = nn.Dropout(attn_dropout)

    def forward(self, q, k, v, mask=None):
        # self.temperature是论文中的d_k ** 0.5，防止梯度过大
        # QxK/sqrt(dk)
        attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
        # torch.matmul(input, other, *, out=None) → Tensor的作用是两个张量的矩阵乘积
        # .transpose按轴交换，函数中的两个参数(索引)是要互换的轴，类似于矩阵的转置，K需要转置后与Q相乘

        if mask is not None:
            # 屏蔽不想要的输出
            attn = attn.masked_fill(mask == 0, -1e9)
            # mask的shape的最大维度必须和attn一样 ，并且元素只能是 0或者1 ，
            # 是 mask中为0的元素所在的索引，在 attn 中相同的的索引处替换为 value
            # 对mask == 0,即mask == False的部分填充 − ∞ ,
            #这样过 σ(⋅)后可以保证为0. 为0, 其信息就不可能被加权到其他词中.

        # softmax+dropout
        attn = self.dropout(F.softmax(attn, dim=-1))
        # 概率分布xV
        output = torch.matmul(attn, v)

        return output, attn

再次复习下 Multi-Head Attention 层的图示，可以发现在前面讲的内容基础上还加入了残差设计和层归一化操作，目的是为了防止梯度消失，加快收敛。

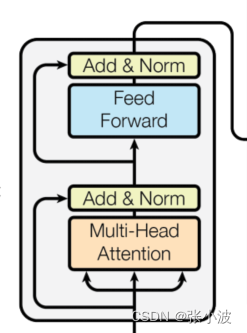
Multi-Head Attention 实现在 ScaledDotProductAttention 基础上构建：

class MultiHeadAttention(nn.Module):
    ''' Multi-Head Attention module '''

    # n_head头的个数，默认是8
    # d_model编码向量长度，例如本文说的512
    # d_k, d_v的值一般会设置为 n_head * d_k=d_model， 8*64=512
    # 此时，Concat后正好和原始输入一样，当然不相同也可以，因为后面有fc层
    # 相当于将可学习矩阵分成独立的n_head份
    def __init__(self, n_head, d_model, d_k, d_v, dropout=0.1):
        super().__init__()
        # 假设n_head=8，d_k=64
        self.n_head = n_head
        self.d_k = d_k
        self.d_v = d_v
        # d_model输入向量，n_head * d_k输出向量
        # 可学习W^Q，W^K,W^V矩阵参数初始化
        self.w_qs = nn.Linear(d_model, n_head * d_k, bias=False)
        self.w_ks = nn.Linear(d_model, n_head * d_k, bias=False)
        self.w_vs = nn.Linear(d_model, n_head * d_v, bias=False)
        # nn.Linear()用于设置网络中的全连接层，需要注意的是全连接层的输入与输出都是二维张量
        # 最后的输出维度变换操作
        self.fc = nn.Linear(n_head * d_v, d_model, bias=False)
        # 单头自注意力
        self.attention = ScaledDotProductAttention(temperature=d_k ** 0.5)
        self.dropout = nn.Dropout(dropout)
        # 层归一化
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
        # nn.LayerNorm 对所有channel的每个像素分别计算
        # 计算一个batch中所有channel中的每一个参数的均值和方差进行归一化

    def forward(self, q, k, v, mask=None):
        # 假设qkv输入是(b,100,512),100是训练每个样本最大单词个数
        # 一般qkv相等，即自注意力
        residual = q
        # 将输入x和可学习矩阵相乘，得到(b,100,512)输出
        # 其中512的含义其实是8x64，8个head，每个head的可学习矩阵为64维度
        # q的输出是(b,100,8,64),kv也是一样 
        # 8是8头注意力的意思，主要还是后面二维的矩阵运算
        q = self.w_qs(q).view(sz_b, len_q, n_head, d_k)
        k = self.w_ks(k).view(sz_b, len_k, n_head, d_k)
        v = self.w_vs(v).view(sz_b, len_v, n_head, d_v)

        # (b,100,8,64)变成(b,8,100,64)，方便后面计算，也就是8个头单独计算
        q, k, v = q.transpose(1, 2), k.transpose(1, 2), v.transpose(1, 2)

        if mask is not None:
            mask = mask.unsqueeze(1)   # For head axis broadcasting.用于头部轴广播 
            # unsqueeze（）是来增加一个维度的
        # 输出 q 是(b,8,100,64),维持不变,内部计算流程是：
        # q*k转置(b,8,64,100)，除以d_k ** 0.5，输出维度是(b,8,100,100),即单词和单词直接的相似性
        # 对最后一个维度进行softmax操作得到(b,8,100,100)
        # 最后乘上V  (b,8,100,64)，得到(b,8,100,64)输出
        q, attn = self.attention(q, k, v, mask=mask)

        # b,100,8,64-->b,100,512  
        q = q.transpose(1, 2).contiguous().view(sz_b, len_q, -1)
        # 重新将词向量维度拉回到 512   ，8头计算完再通道合并
        q = self.dropout(self.fc(q))
        # 残差计算
        q += residual
        # 层归一化，在512维度计算均值和方差，进行层归一化
        q = self.layer_norm(q)
        # LayerNorm：channel方向做归一化，算CHW的均值，主要对RNN作用明显；

        return q, attn

现在pytorch新版本已经把MultiHeadAttention当做nn中的一个类了，可以直接调用。

2.2.2 前馈神经网络层

这个层就没啥说的了，非常简单：
PositionwiseFeedForward 位置前馈

class PositionwiseFeedForward(nn.Module):
    ''' A two-feed-forward-layer module  双前馈层模块'''

    def __init__(self, d_in, d_hid, dropout=0.1):
        super().__init__()
        # 两个fc层，对最后的512维度进行变换
        self.w_1 = nn.Linear(d_in, d_hid) # position-wise
        self.w_2 = nn.Linear(d_hid, d_in) # position-wise
        self.layer_norm = nn.LayerNorm(d_in, eps=1e-6)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        residual = x

        x = self.w_2(F.relu(self.w_1(x)))
        x = self.dropout(x)
        x += residual

        x = self.layer_norm(x)

        return x

2.2.3 编码层操作整体流程

可视化如下所示：

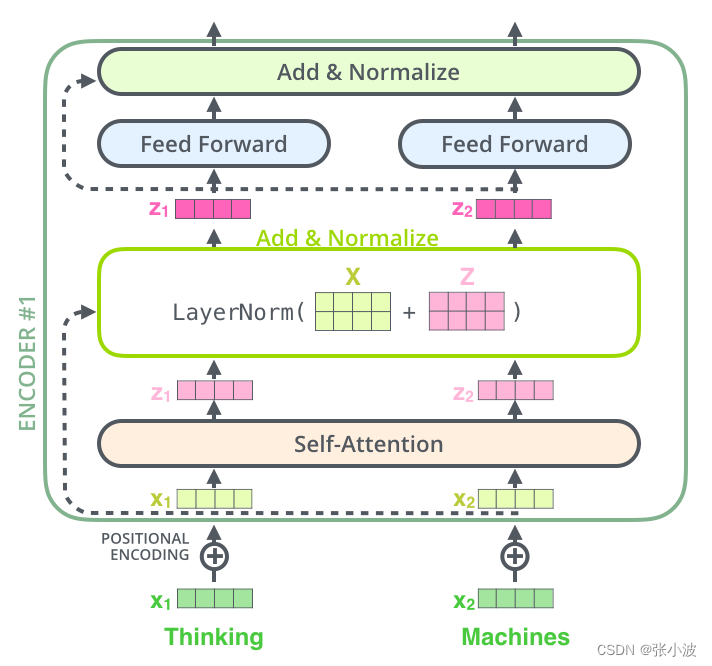
单个编码层代码如下所示：

class EncoderLayer(nn.Module):
    def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
        super(EncoderLayer, self).__init__()
        self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
        self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)

    def forward(self, enc_input, slf_attn_mask=None):
        # Q K V是同一个，自注意力
        # enc_input来自源单词嵌入向量或者前一个编码器输出
        enc_output, enc_slf_attn = self.slf_attn(
            enc_input, enc_input, enc_input, mask=slf_attn_mask)
        enc_output = self.pos_ffn(enc_output)
        return enc_output, enc_slf_attn

将上述编码过程重复n遍即可，除了第一个模块输入是单词嵌入向量与位置编码的和外，其余编码层输入是上一个编码器输出，即后面的编码器输入不需要位置编码向量。
如果考虑n个编码器的运行过程，如下所示：

class Encoder(nn.Module):
    def __init__(
            self, n_src_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
            d_model, d_inner, pad_idx, dropout=0.1, n_position=200):
        # nlp领域的词嵌入向量生成过程(单词在词表里面的索引idx-->d_word_vec长度的向量)
        self.src_word_emb = nn.Embedding(n_src_vocab, d_word_vec, padding_idx=pad_idx)
        # n.embedding就是一个字典映射表，
        # 位置编码
        self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
        self.dropout = nn.Dropout(p=dropout)
        # n个编码器层
        self.layer_stack = nn.ModuleList([
            EncoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
            for _ in range(n_layers)])
        # 层归一化
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)

    def forward(self, src_seq, src_mask, return_attns=False):
        # 对输入序列进行词嵌入，加上位置编码
        enc_output = self.dropout(self.position_enc(self.src_word_emb(src_seq)))
        enc_output = self.layer_norm(enc_output)
        # 作为编码器层输入 ,遍历每个编码器
        for enc_layer in self.layer_stack:
            enc_output, _ = enc_layer(enc_output, slf_attn_mask=src_mask)
        return enc_output

到目前为止，我们就讲完了编码部分的全部流程和代码细节。
现在再来看整个Transformer算法就会感觉亲切、熟悉了很多：

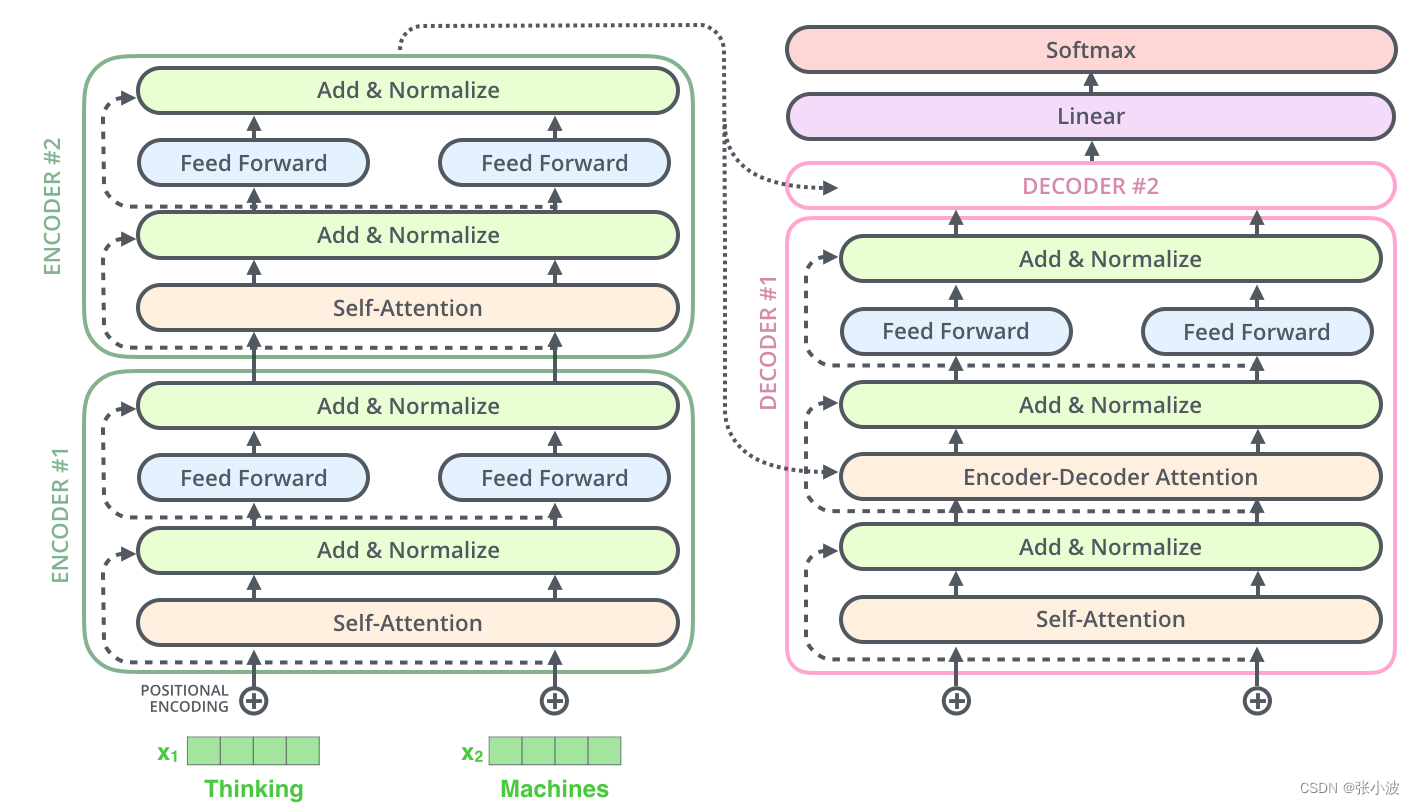
2.3 解码器输入数据处理

在分析解码器结构前先看下解码器整体结构，方便理解：

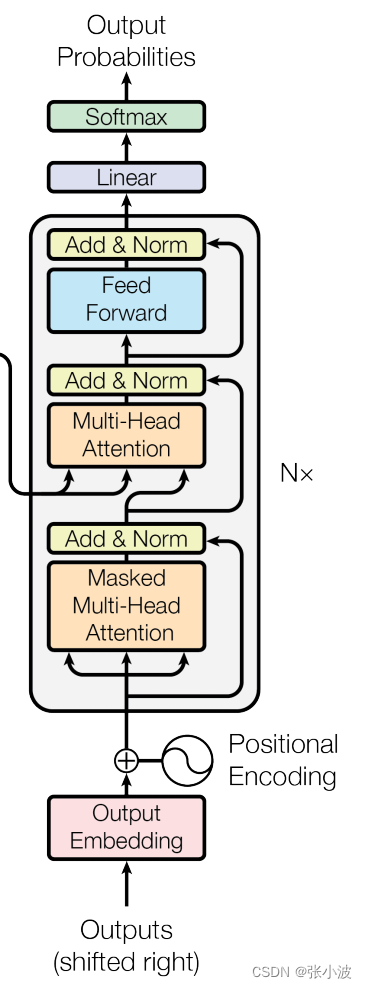
其输入数据处理也要区分第一个解码器和后续解码器，和编码器类似，第一个解码器输入不仅包括最后一个编码器输出，还需要额外的输出嵌入向量，而后续解码器输入是来自最后一个编码器输出和前面解码器输出。

在编码器中只有自注意力和前馈神经网络两个模块，但是在解码器中有三个模块，分别是自注意力层、交叉注意力层和前馈神经网络。文章开头就说过内部都是注意力，只不过qkv的来源不同就有了不同的含义，当qkv来自同一个输入，那么叫做自注意力，当kv和q来做不同模块输出，则可以称为交叉注意力。学习transformer一定要理解qkv以及qkv的来源。

2.3.1 目标单词嵌入

这个操作和源单词嵌入过程完全相同，维度也是512。
假设输出是 i am a student，那么需要对这4个单词也利用word2vec算法转化为4x512的矩阵，作为第一个解码器的单词嵌入输入。

2.3.2 位置编码

同样的也需要对解码器输入引入位置编码，做法和编码器部分完全相同，且将目标单词嵌入向量和位置编码向量相加即可作为第一个解码器输入。

和编码器单词嵌入不同的地方是在进行目标单词嵌入前，还需要将目标单词，
即是 i am a student 右移动一位，新增加的一个位置采用提前定义好的标志位BOS_WORD代替，现在就变成 [BOS_WORD, i, am, a, student ] ，为啥要右移？
因为，解码过程和seq2seq一样是顺序解码的，需要提供一个开始解码标志，不然，第一个时间步的解码单词 i 是如何输出的呢？
具体解码过程：

1. 输入BOS_WORD，解码器输出 i；
2. 输入前面已经解码的BOS_WORD 和 i，解码器输出 am；… … … …
3. 输入已经解码的BOS_WORD、i、am、a 和 student，解码器输出解码结束标志位EOS_WORD, 每次解码都会利用前面已经解码输出的所有单词嵌入信息。

下面有个非常清晰的GIF图，一目了然：

图示，解码步骤1：输入BOS_WORD，解码器输出 i :

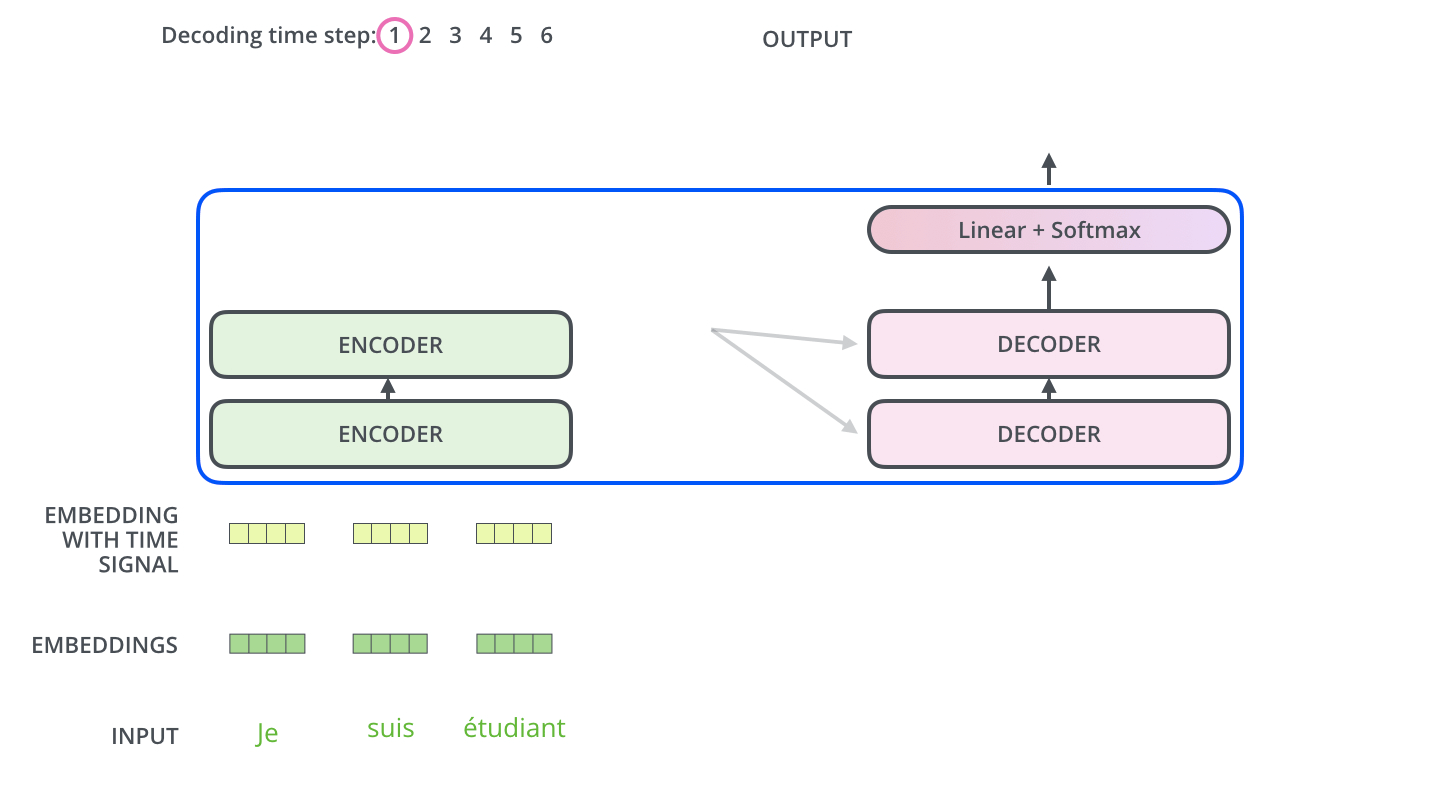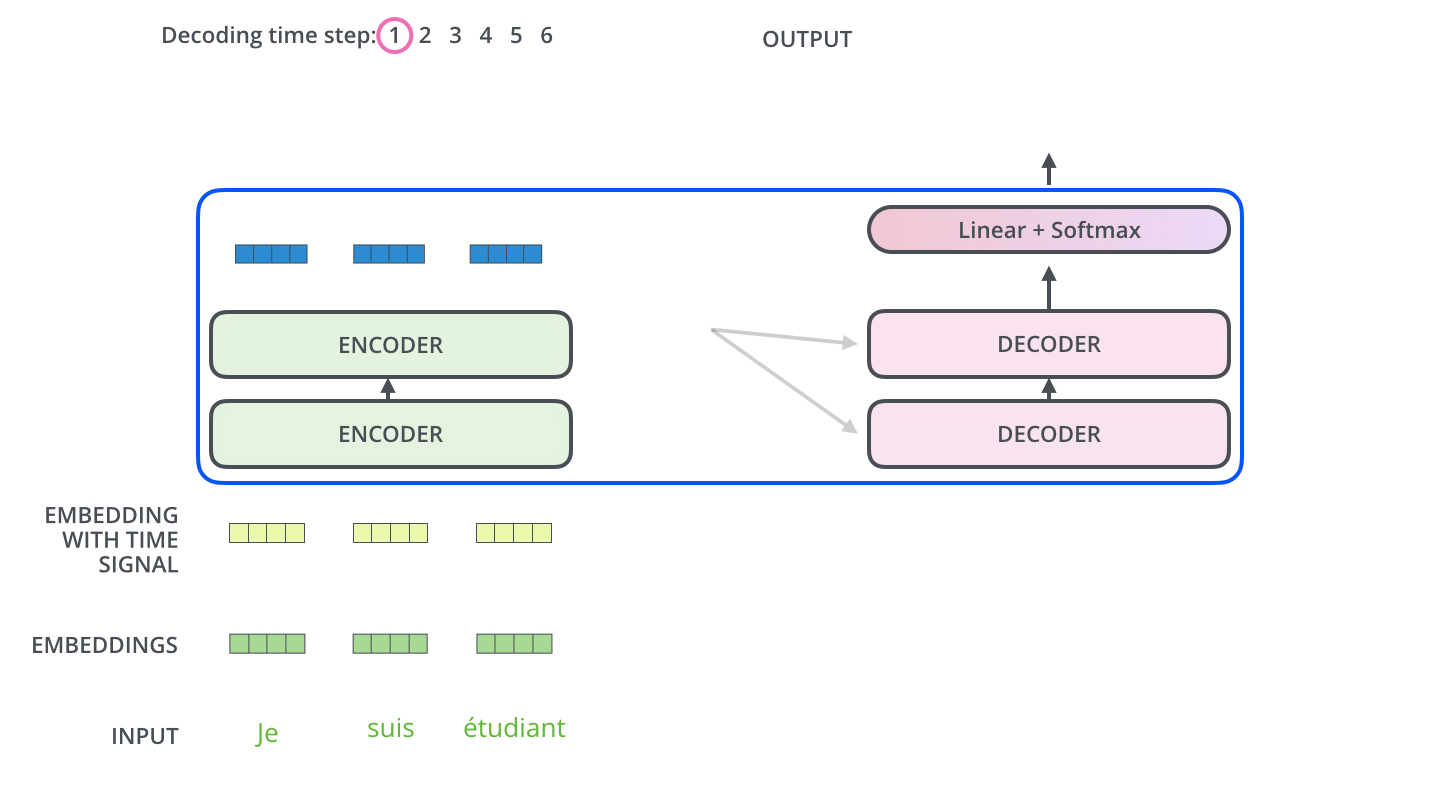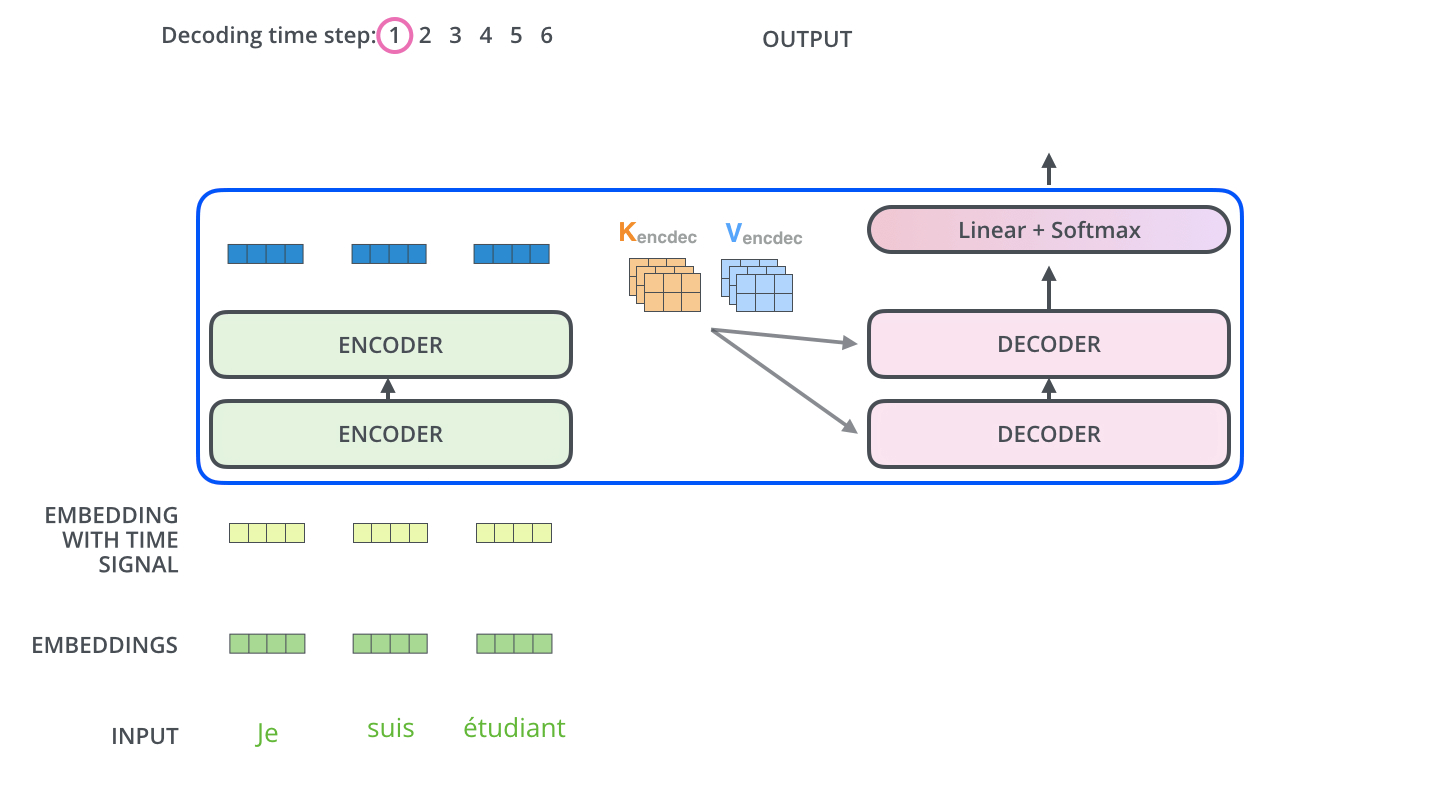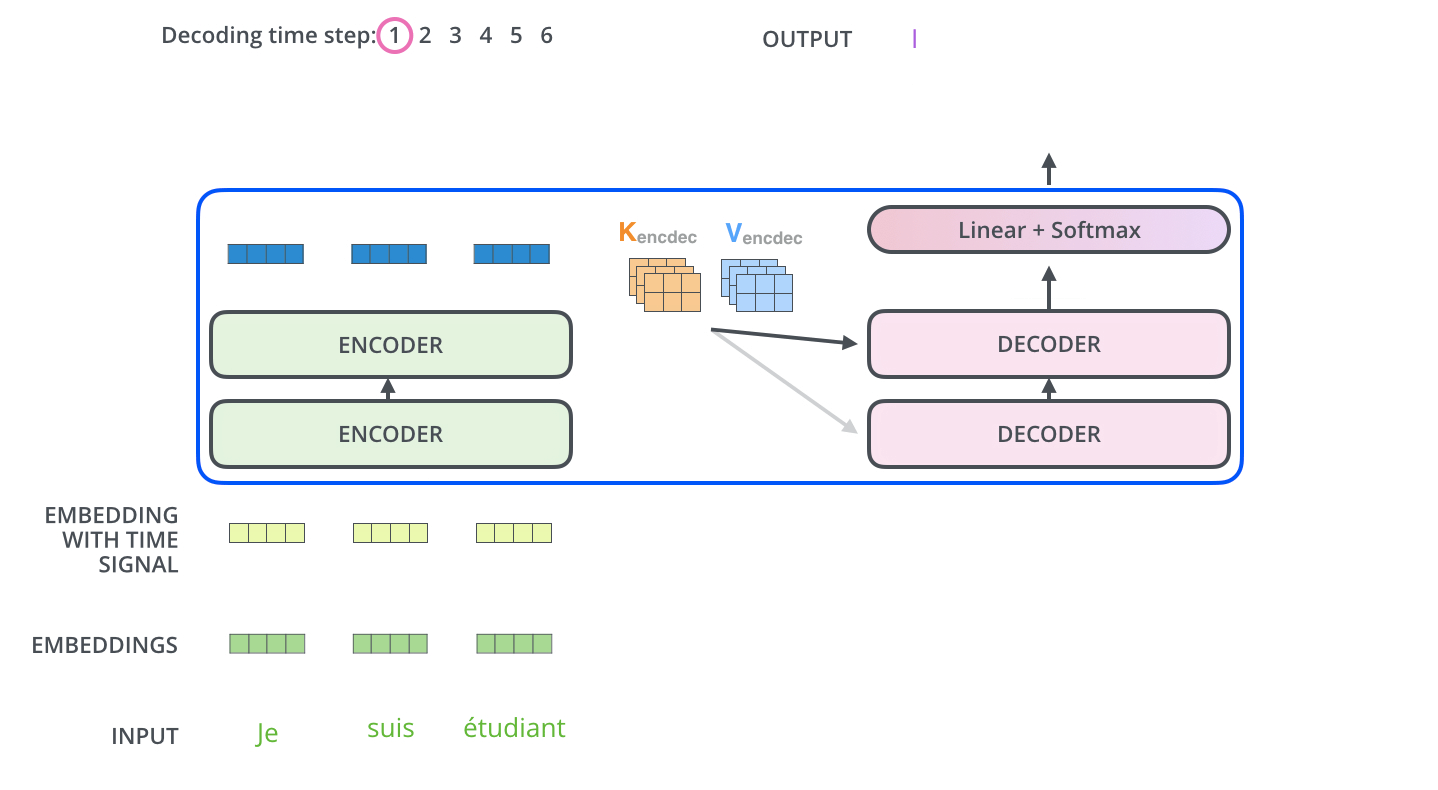
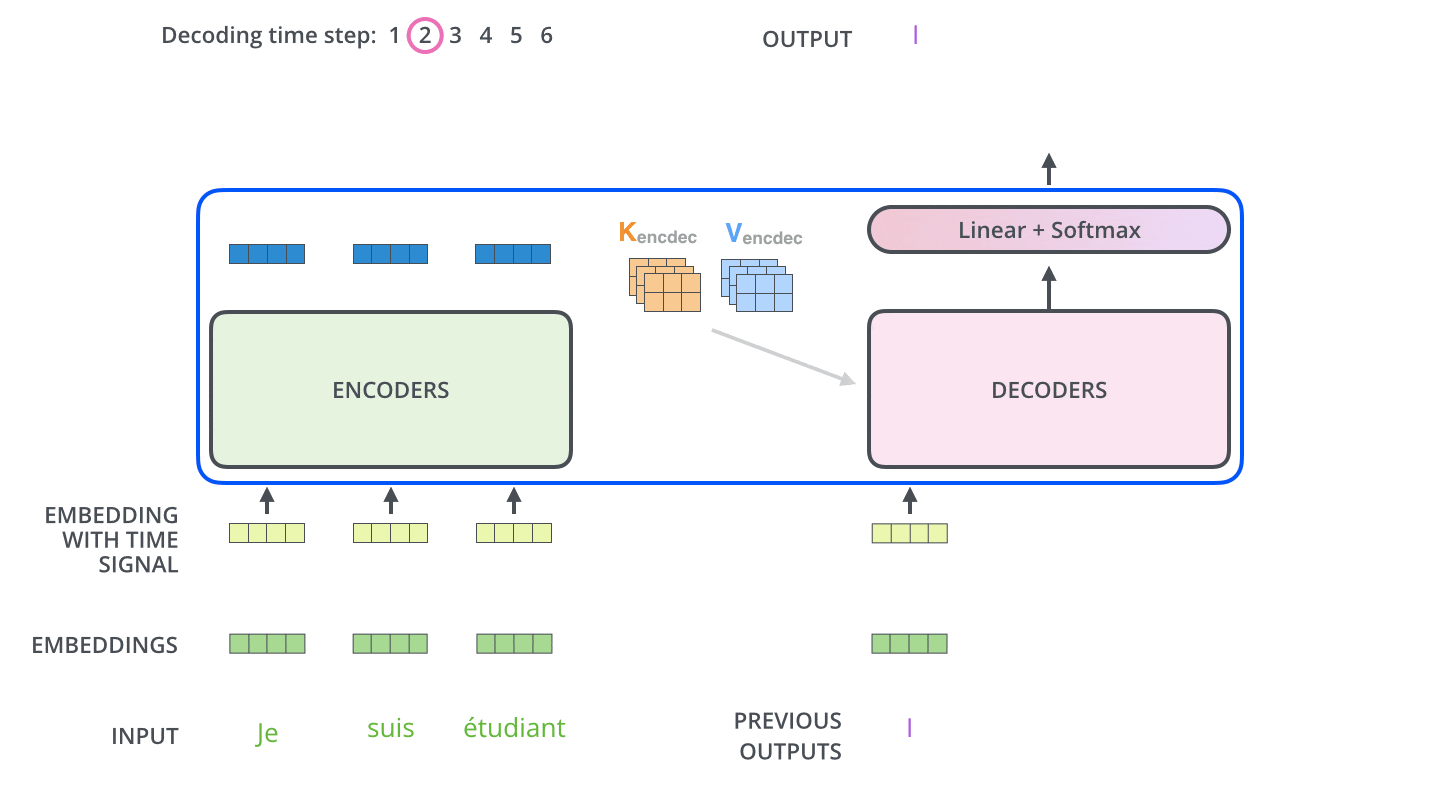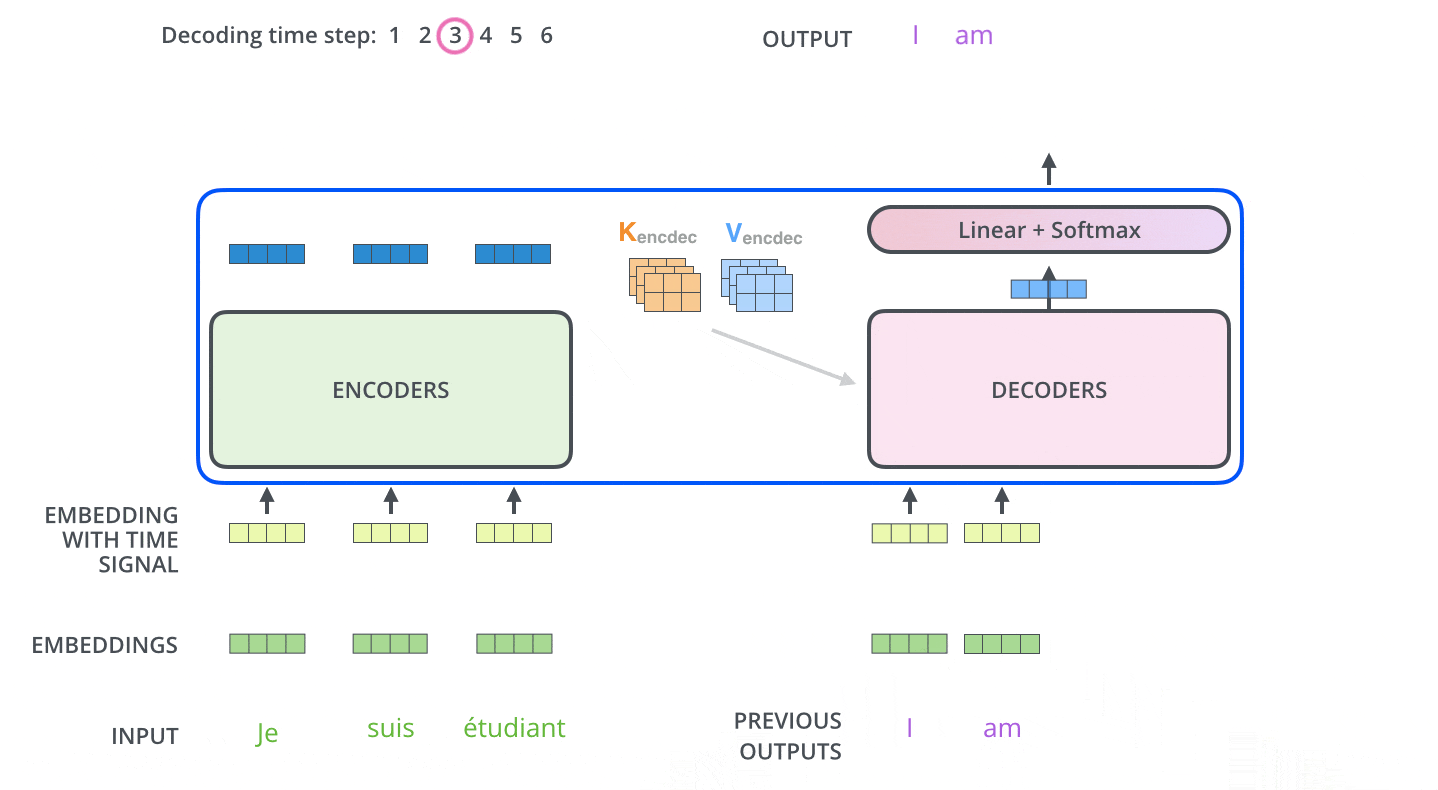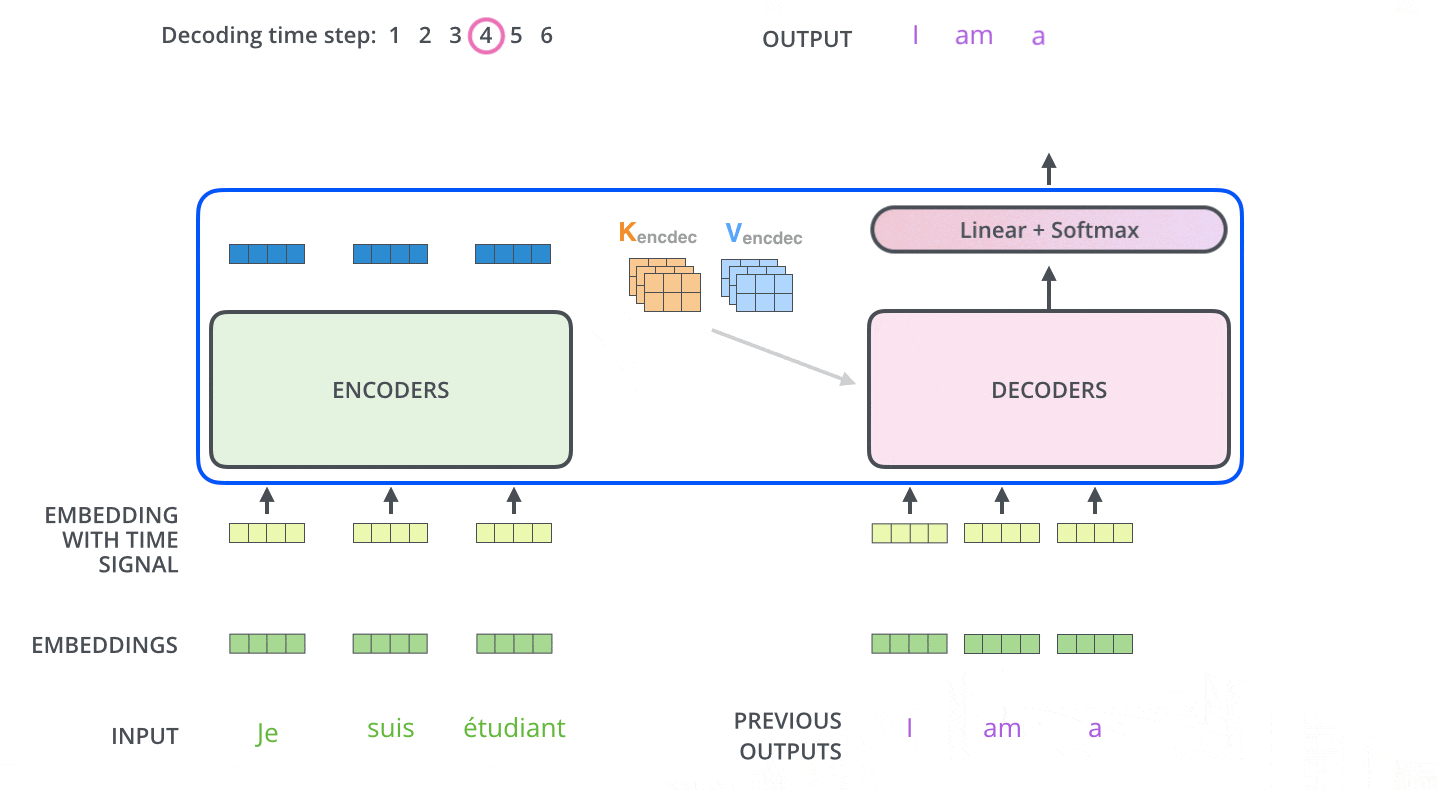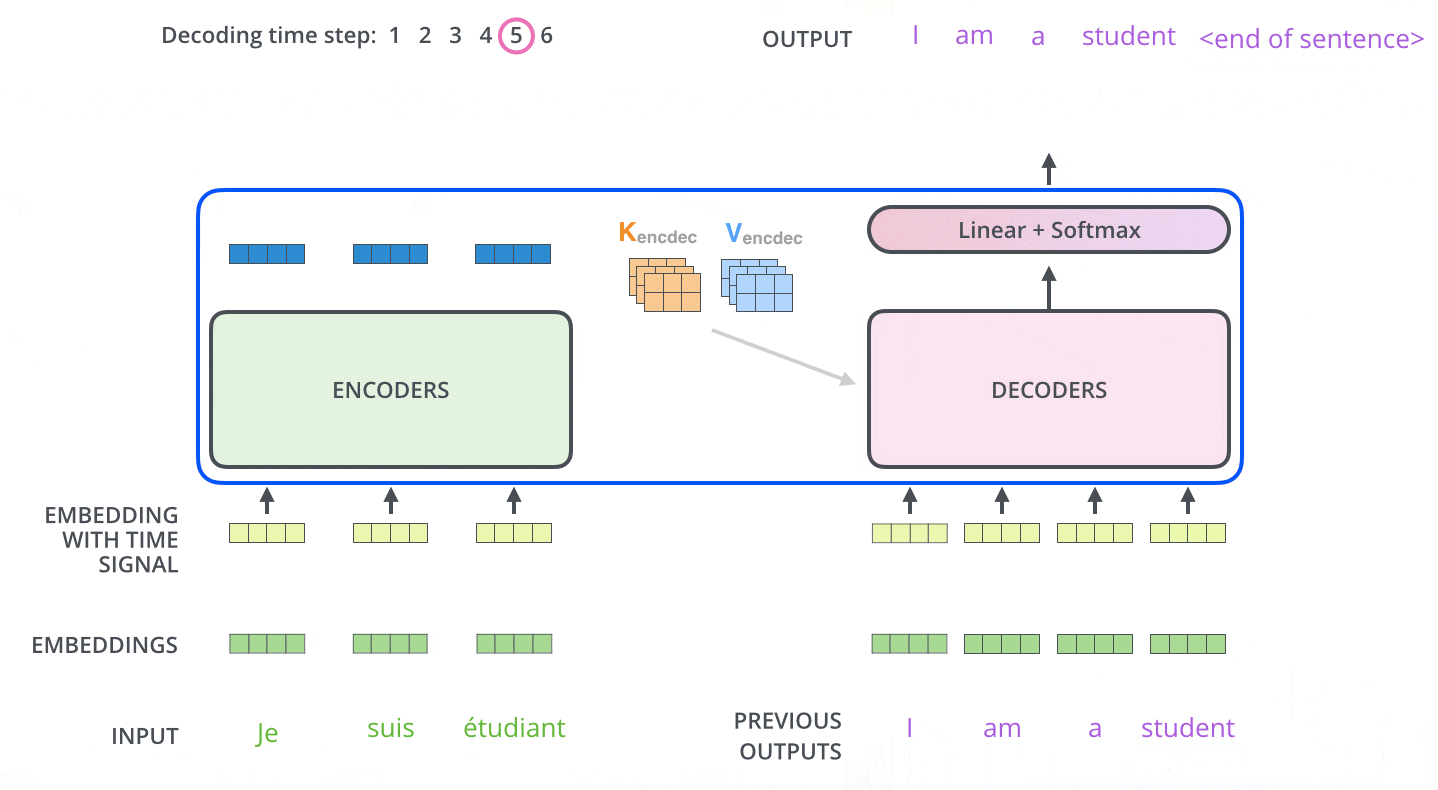
图示，解码步骤2和3：

2.4 解码器前向过程

仔细观察解码器结构，其包括：
带有mask的MultiHeadAttention、MultiHeadAttention 和 前馈神经网络层 三个组件，

带有mask的MultiHeadAttention和MultiHeadAttention结构和代码写法是完全相同，唯一区别是是否输入了mask。

为啥要mask？
原因依然是顺序解码导致的。
试想模型训练好了，开始进行翻译(测试)，其流程就是上面写的：
输入BOS_WORD，解码器输出i；
输入前面已经解码的BOS_WORD和i，解码器输出am…，
输入已经解码的BOS_WORD、i、am、a和student，解码器输出解码结束标志位EOS_WORD,
每次解码都会利用前面已经解码输出的所有单词嵌入信息，这个测试过程是没有问题，但是，训练时候我肯定不想采用上述顺序解码，类似rnn 即一个一个目标单词嵌入向量顺序输入训练，肯定想采用类似编码器中的矩阵并行算法，一步就把所有目标单词预测出来。
要实现这个功能就可以参考编码器的操作，把目标单词嵌入向量组成矩阵一次输入即可，但是在解码 am 时候，不能利用到后面单词 a 和 student 的目标单词嵌入向量信息，否则这就是作弊(测试时候不可能能未卜先知)。为此引入mask，目的是构成下三角矩阵，右上角全部设置为负无穷(相当于忽略)，从而实现当解码第一个字的时候，第一个字只能与第一个字计算相关性，当解出第二个字的时候，只能计算出第二个字与第一个字和第二个字的相关性。
具体是：
在解码器中，自注意力层只被允许处理输出序列中，更靠前的那些位置，在softmax步骤前，它会把后面的位置给隐去（把它们设为-inf）。

还有个非常重要点需要知道(看2.3第一个图的图示可以发现)：
解码器内部的带有mask的MultiHeadAttention的 q k v 向量输入来自目标单词嵌入或者前一个解码器输出， 三者是相同的，但是后面的MultiHeadAttention的 q k v向量中的 k v 来自最后一层编码器的输入，而** q 来自带有mask的MultiHeadAttention模块的输出。**

知识点：下三角矩阵

下三角为权值，上三角全相同（例如全为0或1）

例如：

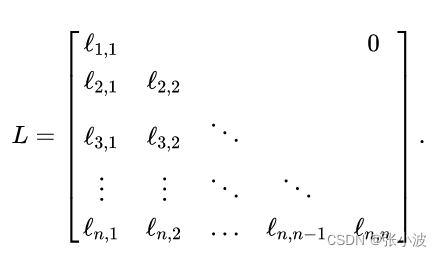
或者：

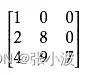
以上均为下三角矩阵。

关于带mask的注意力层写法，其实就是前面提到的代码：
（与2.2.1的第一个代码块一致）

class ScaledDotProductAttention(nn.Module):
    ''' Scaled Dot-Product Attention 缩放点积注意力'''

    def __init__(self, temperature, attn_dropout=0.1):
        super().__init__()
        self.temperature = temperature
        self.dropout = nn.Dropout(attn_dropout)

    def forward(self, q, k, v, mask=None):
        # 假设q是b,8,10,64(b是batch，8是head个数，10是样本最大单词长度，
        # 64是每个单词的编码向量)
        # q (b,8,10,64) k (b,8,10,64) k的转置(b,8,64,10)
        # attn输出维度是b,8,10,10  
        attn = torch.matmul(q / self.temperature, k.transpose(2, 3))
        # torch.matmul(input, other, *, out=None) → Tensor的作用是两个张量的矩阵乘积
        # .transpose按轴交换，函数中的两个参数(索引)是要互换的轴，类似于矩阵的转置，K需要转置后与Q相乘

        # 故mask维度也是b,8,10,10
        # 忽略b,8，只关注10x10的矩阵，其是下三角矩阵，下三角位置全1，其余位置全0
        if mask is not None:
            # 提前算出mask，将为0的地方变成极小值-1e9，把这些位置的值设置为忽略
            # 目的是避免解码过程中利用到未来信息
            attn = attn.masked_fill(mask == 0, -1e9)
            # masked_fill函数是 mask中为0的元素所在的索引，在 attn 中相同的的索引处替换为 value
            # 对mask == 0,即mask == False的部分填充 − ∞ ,
            #这样过 σ(⋅)后可以保证为0. 为0, 其信息就不可能被加权到其他词中.
        # softmax+dropout
        attn = self.dropout(F.softmax(attn, dim=-1))
        output = torch.matmul(attn, v)

        return output, attn

可视化如下：图片来源https://zhuanlan.zhihu.com/p/44731789

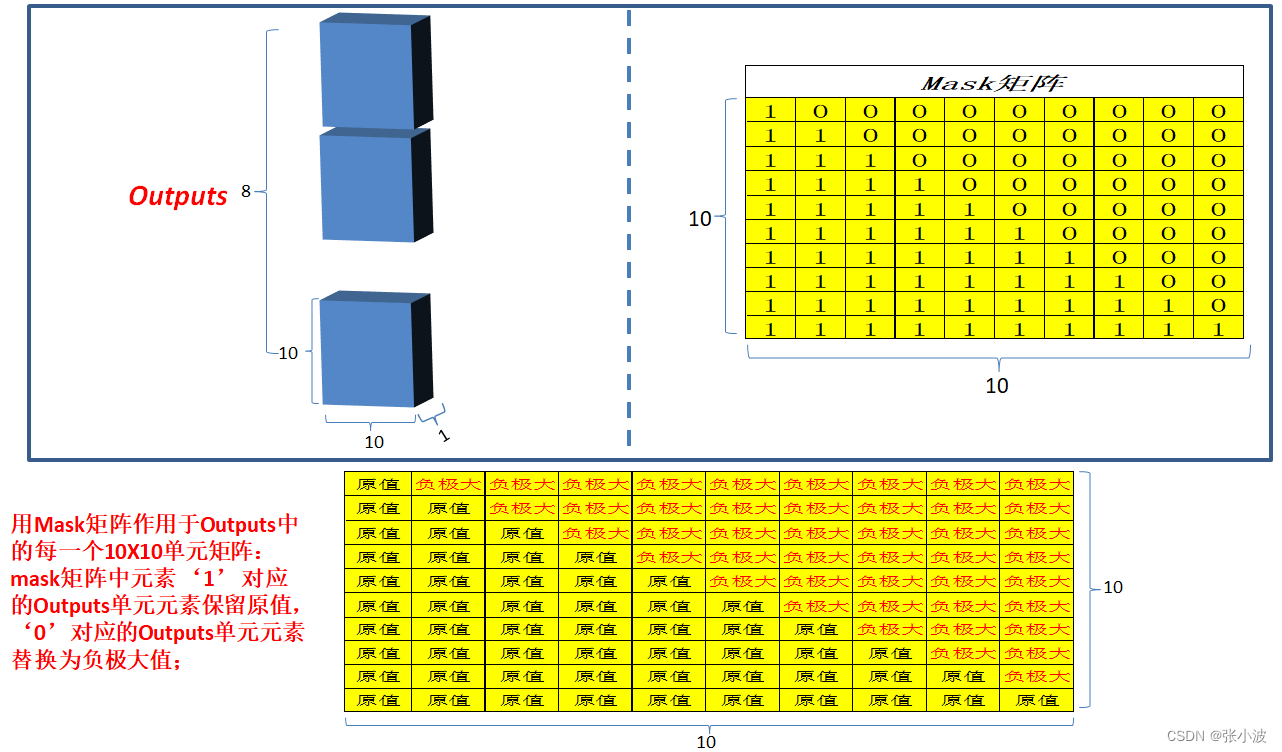
整个解码器代码和编码器非常类似：

class DecoderLayer(nn.Module):
    ''' Compose with three layers '''

    def __init__(self, d_model, d_inner, n_head, d_k, d_v, dropout=0.1):
        super(DecoderLayer, self).__init__()
        self.slf_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
        self.enc_attn = MultiHeadAttention(n_head, d_model, d_k, d_v, dropout=dropout)
        self.pos_ffn = PositionwiseFeedForward(d_model, d_inner, dropout=dropout)

    def forward(
            self, dec_input, enc_output,
            slf_attn_mask=None, dec_enc_attn_mask=None):
        # 标准的自注意力，QKV=dec_input来自目标单词嵌入或者前一个解码器输出
        dec_output, dec_slf_attn = self.slf_attn(
            dec_input, dec_input, dec_input, mask=slf_attn_mask)
        # （重点！！！）KV来自最后一个编码层输出enc_output，Q来自带有mask的self.slf_attn输出
        dec_output, dec_enc_attn = self.enc_attn(
            dec_output, enc_output, enc_output, mask=dec_enc_attn_mask)
        # slf_attn_mask 与 dec_enc_attn_mask 可能不同   
        dec_output = self.pos_ffn(dec_output)
        return dec_output, dec_slf_attn, dec_enc_attn

考虑n个解码器模块，其整体流程为：

class Decoder(nn.Module):
    def __init__(
            self, n_trg_vocab, d_word_vec, n_layers, n_head, d_k, d_v,
            d_model, d_inner, pad_idx, n_position=200, dropout=0.1):
        # 目标单词嵌入
        self.trg_word_emb = nn.Embedding(n_trg_vocab, d_word_vec, padding_idx=pad_idx)
        # 位置嵌入向量
        self.position_enc = PositionalEncoding(d_word_vec, n_position=n_position)
        self.dropout = nn.Dropout(p=dropout)
        # n个解码器
        self.layer_stack = nn.ModuleList([
            DecoderLayer(d_model, d_inner, n_head, d_k, d_v, dropout=dropout)
            for _ in range(n_layers)])
        # 层归一化
        self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)

    def forward(self, trg_seq, trg_mask, enc_output, src_mask, return_attns=False):
        # 目标单词嵌入+位置编码
        dec_output = self.dropout(self.position_enc(self.trg_word_emb(trg_seq)))
        dec_output = self.layer_norm(dec_output)
        # 遍历每个解码器
        for dec_layer in self.layer_stack:  
            # 需要输入3个信息：目标单词嵌入+位置编码、最后一个编码器输出enc_output
            # 和dec_enc_attn_mask，解码时候不能看到未来单词信息
            dec_output, dec_slf_attn, dec_enc_attn = dec_layer(
                dec_output, enc_output, slf_attn_mask=trg_mask, dec_enc_attn_mask=src_mask)
        return dec_output

2.5 分类器

在进行编码器-解码器后输出依然是向量，需要在后面接fc+softmax层进行分类训练。
假设当前训练过程是翻译任务需要输出 i am a student EOS_WORD 这5个单词。
假设我们的模型是从训练集中学习一万个不同的英语单词（我们模型的“输出词表”）。
因此，softmax后输出为一万个单元格长度的向量，每个单元格对应某一个单词的分数，这其实就是普通多分类问题，只不过维度比较大而已。

依然以前面例子为例，假设编码器输出shape是(b,100,512)，经过fc后变成(b,100,10000)，然后对最后一个维度进行softmax操作，得到 b x 100个单词的概率分布，在训练过程中 b x 100个单词是知道label的，故可以直接采用ce loss进行训练。

self.trg_word_prj = nn.Linear(d_model, n_trg_vocab, bias=False)
dec_output, *_ = self.model.decoder(trg_seq, trg_mask, enc_output, src_mask)
return F.softmax(self.model.trg_word_prj(dec_output), dim=-1)

2.6 前向流程

以翻译任务为例：

• 将源单词进行嵌入，组成矩阵(加上位置编码矩阵)输入到n个编码器中，输出编码向量KV
• 第一个解码器先输入一个BOS_WORD单词嵌入向量，后续解码器接受该解码器输出，结合KV进行第一次解码
• 将第一次解码单词进行嵌入，联合BOS_WORD单词嵌入向量，构成矩阵，再次输入到解码器中进行第二次解码，得到解码单词
• 不断循环，每次的第一个解码器输入都不同，其包含了前面时间步长解码出的所有单词
• 直到输出EOS_WORD表示解码结束或者强制设置最大时间步长即可

这个解码过程其实就是标准的seq2seq流程。到目前为止就描述完了整个标准transformer训练和测试流程。

---

上一篇：学习视觉CV Transformer （1）–Transformer介绍

下一篇：学习视觉CV Transformer （3）–ViT、DETR的原理及代码分析