数组与链表算法-矩阵算法

news2024/11/24 1:34:02

目录

 数组与链表算法-矩阵算法

矩阵相加

C++代码

矩阵相乘

C++代码

转置矩阵

C++代码

稀疏矩阵

C++代码

 数组与链表算法-矩阵算法

矩阵相加

矩阵的相加运算较为简单，前提是相加的两个矩阵对应的行数与列数必须相等，而相加后矩阵的行数与列数也是相同的。【

C++代码

#include<iostream>
using namespace std;

void MaterixAdd(int* arrA, int* arrB, int* arrC, int dimX, int dimY) {
	if (dimX <= 0 || dimY <= 0) {
		cout << "矩阵维数必须大于0" << endl;
		return;
	}
	for (int row = 0; row < dimX; row++) {
		for (int col = 0; col < dimY; col++) {
			arrC[row * dimX + col] = arrA[row * dimX + col] + arrB[row * dimX + col];
		}
	}
}

void PrintArr(int* arr, int dimX, int dimY) {
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimY; j++) {
			cout << arr[i * dimX + j] << "\t";
		}
		cout << endl;
	}
}

int main() {
	const int Row = 3;
	const int Col = 3;

	int A[Row][Col] = { {1,3,5},
						{7,9,11},
						{13,15,17} };
	int B[Row][Col] = { {9,8,7},
						{6,5,4},
						{3,2,1} };
	int C[Row][Col] = { 0 };
	cout << "矩阵A的各个元素：" << endl;
	PrintArr(&A[0][0], Row, Col);
	cout << "矩阵B的各个元素：" << endl;
	PrintArr(&B[0][0], Row, Col);
	MaterixAdd(&A[0][0], &B[0][0], &C[0][0], Row, Col);
	cout << "矩阵C的各个元素：" << endl;
	PrintArr(&C[0][0], Row, Col);
	return 0;
}

输出结果

 

 

矩阵相乘

两个矩阵A和B的相乘受到某些条件的限制。首先，必须符合A为一个m\times n的矩阵，B为一个n\times p的矩阵，A\times B之后的结果为一个m\times p的矩阵C。

C++代码

#include<iostream>
using namespace std;

void MaterixMultiply(int* arrA, int* arrB, int* arrC, int dimX, int dimY) {
	if (dimX <= 0 || dimY <= 0) {
		cout << "矩阵维数必须大于0" << endl;
		return;
	}
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimX; j++) {
			int Temp = 0;
			for(int k = 0;k< dimY;k++){
				arrC[i * dimX + j] += (arrA[i * dimY + k] * arrB[k * dimX + j]);
			}
		}
	}
}

void PrintArr(int* arr, int dimX, int dimY) {
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimY; j++) {
			cout << arr[i * dimY + j] << "\t";
		}
		cout << endl;
	}
}

int main() {
	const int Row = 2;
	const int Col = 3;

	int A[Row][Col] = { {1,2,3},
						{4,5,6} };
	int B[Col][Row] = { {3,4},
						{6,1},
						{2,7} };
	int C[Row][Row] = { 0 };
	cout << "矩阵A的各个元素：" << endl;
	PrintArr(&A[0][0], Row, Col);
	cout << "矩阵B的各个元素：" << endl;
	PrintArr(&B[0][0], Col, Row);
	MaterixMultiply(&A[0][0], &B[0][0], &C[0][0], Row, Col);
	cout << "矩阵C的各个元素：" << endl;
	PrintArr(&C[0][0], Row, Row);
	return 0;
}

输出结果

转置矩阵

转置矩阵（A^{t}）就是把原矩阵的行坐标元素与列坐标元素相互调换。假设A^{t}为A的转置矩阵，则有A^{t}[j,i] = A[i,j]。

C++代码

#include<iostream>
using namespace std;

void MaterixTranspose(int* arr, int dimX, int dimY) {
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j <= i; j++) {
			int Temp = arr[i * dimY + j];
			arr[i * dimY + j] = arr[j * dimY + i];
			arr[j * dimY + i] = Temp;
		}
	}
}

void PrintArr(int* arr, int dimX, int dimY) {
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimY; j++)
			cout << arr[i * dimY + j] << "\t";
		cout << endl;
	}
}

int main() {
	const int Row = 3;
	const int Col = 3;

	int arr[Row][Col] = { {1,2,3},
						  {4,5,6},
						  {7,8,9} };
	cout << "原始矩阵：" << endl;
	PrintArr(&arr[0][0], Row, Col);
	MaterixTranspose(&arr[0][0], Row, Col);
	cout << "转置矩阵：" << endl;
	PrintArr(&arr[0][0], Row, Col);
	return 0;
}

输出结果

稀疏矩阵

稀疏矩阵（Sparse Matrix）就是指一个矩阵中的大部分元素为0。对于稀疏矩阵而言，因为矩阵中的许多元素都是0，所以实际存储的数据项很少，如果在计算机中使用传统的二维数组方式来存储稀疏矩阵，就十分浪费计算机的内存空间。

提高内存空间利用率的方法是使用三项式（3-Tuple）的数据结构。我们把每一个非零项用（i, j, item-value）的形式来表示，假如一个稀疏矩阵有n个非零项，那么可以使用一个A(0:n, 1:3)的二维数组来存储这些非零项。

其中，A(0, 1)存储这个稀疏矩阵的行数，A(0，2)存储这个稀疏矩阵的列数，而A(0，3)则存储这个稀疏矩阵非零项的总数。另外，每一个非零项以（i, j, item-value）来表示。其中i为此矩阵非零项所在的行数，j为此矩阵非零项所在的列数，item-value则为此矩阵非零项的值。

A(0, 1)：表示此矩阵的行数。

A(0, 2)：表示此矩阵的列数。

A(0, 3)：表示此矩阵非零项的总数。

这种利用3项式数据结构来压缩稀疏矩阵的方式可以减少对内存的浪费。

C++代码

#include<iostream>
using namespace std;

void MaterixSparse(int* arrSparse, int* arrCompress, int dimX, int dimY) {
	int temp = 1;
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimY; j++) {
			if (arrSparse[i * dimY + j] != 0) {
				arrCompress[temp * 3 + 0] = i;
				arrCompress[temp * 3 + 1] = j;
				arrCompress[temp * 3 + 2] = arrSparse[i * dimY + j];
				temp++;
			}
		}
	}
}

void PrintArr(int* arr, int dimX, int dimY) {
	for (int i = 0; i < dimX; i++) {
		for (int j = 0; j < dimY; j++)
			cout << arr[i * dimY + j] << "\t";
		cout << endl;
	}
}

int main() {
	const int Row = 8;
	const int Col = 9;
	const int NotZero = 8;

	int Sparse[Row][Col] = { {0,0,0,0,0,0,0,0,0},
						     {0,0,0,0,0,0,0,0,0},
						     {0,0,0,0,7,0,0,0,0},
						     {0,0,0,0,0,0,0,0,5}, 
						     {0,0,0,0,0,0,0,0,0}, 
						     {0,0,0,0,0,0,0,0,0}, 
						     {0,0,6,1,8,0,0,0,2}, 
						     {4,0,0,0,0,0,3,0,0} };
	int Compress[NotZero + 1][3]{ 0 };
	Compress[0][0] = Row;
	Compress[0][1] = Col;
	Compress[0][2] = NotZero;
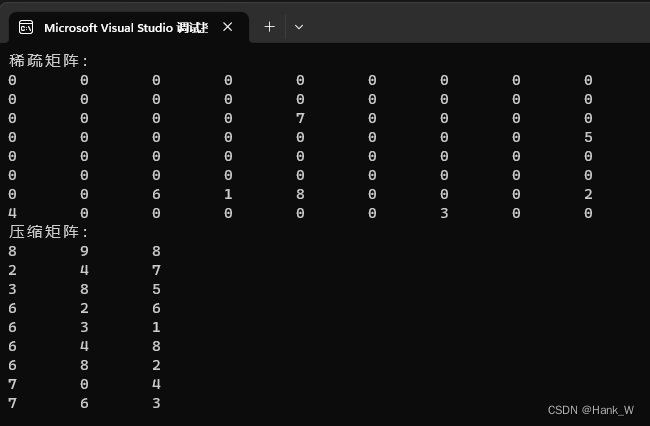
	cout << "稀疏矩阵：" << endl;
	PrintArr(&Sparse[0][0], Row, Col);
	MaterixSparse(&Sparse[0][0], &Compress[0][0], Row, Col);
	cout << "压缩矩阵：" << endl;
	PrintArr(&Compress[0][0], NotZero + 1, 3);
	return 0;
}

输出结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1144495.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Notepad-- 轻量级文本编辑器的安装及基本使用

Notepad-- 轻量级文本编辑器的安装及基本使用

Notepad-- 轻量级文本编辑器的安装及基本使用 一、notepad--介绍1.1 notepad--简介1.2 notepad--特点 二、安装Notepad--2.1 下载Notepad--软件包2.2 解压软件包2.3 运行Notepad-- 三、Notepad-- 的日常使用3.1 编写yaml文件3.2 编写shell脚本文件3.3 编写python测试文件 四、文…
阅读更多...
有关多线程环境下的Volatile、lock、Interlocked和Synchronized们

有关多线程环境下的Volatile、lock、Interlocked和Synchronized们

&#x1f4e2;欢迎点赞 &#xff1a;&#x1f44d; 收藏 ⭐留言 &#x1f4dd; 如有错误敬请指正&#xff0c;赐人玫瑰&#xff0c;手留余香&#xff01;&#x1f4e2;本文作者&#xff1a;由webmote 原创&#x1f4e2;作者格言&#xff1a;新的征程&#xff0c;我们面对的不仅…
阅读更多...
安装使用vcpkg的简易教程

安装使用vcpkg的简易教程

目录 1. 首先安装vcpkg2. 在vcpkg目录下运行bootstrap-vcpkg.bat 命令3. 接着vs进行集成4. 使用vcpkg搜索可用的包5.下载安装所需包6.下载安装完成 1. 首先安装vcpkg 使用git命令下载 git clone https://github.com/Microsoft/vcpkg.git如果下载失败可直接下载文件 (vcpkg-ma…
阅读更多...
美术如何创建 skybox 贴图资源？

美术如何创建 skybox 贴图资源？

文章目录 目的PS手绘Panorama To CubemapPS手绘Pano2VRSkybox & Cubemap Tutorial (Maya & Photoshop)Unity 中使用 ReflectionProbe 生成 Cubemap 然后再 PS 调整PS直接手绘 cubemapBlender 导入 Panorama&#xff0c;然后烘焙到 cubemap&#xff0c;再导入unity中使用…
阅读更多...
git教程(1)---本地仓库操作

git教程(1)---本地仓库操作

git教程 git安装-Centos基本操作git initgit config工作区和版本库工作区暂存区/索引版本库 添加文件---场景一git statusgit log查看.git目录结构 添加文件---场景二修改文件版本回退撤销修改场景一只有工作区有code工作区和暂存区有code所有区域都有code并且没有push到远程仓…
阅读更多...
【Java网络原理】 五

【Java网络原理】 五

本文主要介绍了TCP传输控制协议的报头字段意义以及TCP协议的十大核心特性。 一.TCP传输控制协议 1.TCP报文格式 >端口 范围是0-65535 &#xff0c;只有确定了端口号&#xff0c;才知道把数据报交给哪个应用程序。 >4位首部长度 TCP报头是变长的&#xff0c; 4bit的范…
阅读更多...
Servlet核心API

Servlet核心API

目录 HttpServlet init destory service 实例&#xff1a;处理get、post、put、delete请求 1.通过postman得到请求 2.通过ajax得到请求 HttpServletRequest 常见方法 前端给后端传参 1.GET,query string 2.POST,form 3.POST&#xff0c;json HttpSeverletRespons…
阅读更多...
数据类型与运算符-java

数据类型与运算符-java

数据类型与运算符 1、变量和类型 1.1、整形变量 基本语法格式&#xff1a; int 变量名 初始值;代码示例&#xff1a; int num 10 //定义一个整型变量 System.out.println(num);注意&#xff1a; 1&#xff09;java中&#xff0c;一个int变量占4个字节&#xff0c;和操作…
阅读更多...
【ChatGPT系列】ChatGPT：创新工具还是失业威胁？

【ChatGPT系列】ChatGPT：创新工具还是失业威胁？

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…
阅读更多...
进程、线程、处理机调度

进程、线程、处理机调度

程序&#xff1a;存放在磁盘中的可执行二进制文件&#xff08;即*.exe文件&#xff0c;包含一系列指令集合&#xff09;。是静态的。 进程&#xff1a;程序的一次执行过程。是动态的。同一个程序多次执行将对应多个进程。 线程&#xff1a;轻量级进程。一个进程至少有一个线程…
阅读更多...
qml之ui控件

qml之ui控件

文章目录 ui控件移动版风格嵌套页面并排界面 ui控件 Qt Quick控件用于创建由标准化组件&#xff08;如按钮、标签、滑块等&#xff09;构建的用户界面。 QtQuick.Controls&#xff1a;基本控件。QtQuick.Templates&#xff1a;为控件提供行为化的、非可化视的基本类型。QtQui…
阅读更多...
STM32 CAN使用

STM32 CAN使用

STM32 CAN使用 简介各种通讯接口对比报文总线上的报文信息表示为几种固定的赖类型数据帧列表模式掩码模式配置CAN配置参数位时序 简介 控制器局域网CAN&#xff08;Controller Area Network)是由德国博世公司为汽车应用而开发的多主机局部网络&#xff0c;用于汽车的监测和控制…
阅读更多...
React 生成传递给无障碍属性的唯一 ID

React 生成传递给无障碍属性的唯一 ID

useId() 在组件的顶层调用 useId 生成唯一 ID&#xff1a; import { useId } from react; function PasswordField() { const passwordHintId useId(); // ...参数 useId 不带任何参数。 返回值 useId 返回一个唯一的字符串 ID&#xff0c;与此特定组件中的 useI…
阅读更多...
【CSS】包含块

【CSS】包含块

CSS规范中的包含块 包含块的内容&#xff1a; 元素的尺寸和位置&#xff0c;会受它的包含块所影响。 对于一些属性&#xff0c;例如 width, height, padding, margin&#xff0c;绝对定位元素的偏移值&#xff08;比如 position 被设置为 absolute 或 fixed&#xff09;&…
阅读更多...
『第十章』仪态万千的雨燕：UIKit 和 SwiftUI

『第十章』仪态万千的雨燕：UIKit 和 SwiftUI

在本篇博文中,您将学到如下内容: 1. 老骥伏枥：AppKit 和 UIKit2. 雨燕的新装：SwiftUI3. SwiftUI 原生视图4. SwiftUI 容器4.1 ViewThatFits4.2 自定义布局（Custom Layout）6. SwiftUI 修改器（Modifiers）6.1 修改器修饰作用域6.1 自定义修改器5. SwiftUI 状态：真相之源（S…
阅读更多...
在spring boot+vue项目中@CrossOrigin 配置了允许跨域但是依然报错跨域，解决跨域请求的一次残酷经历

在spring boot+vue项目中@CrossOrigin 配置了允许跨域但是依然报错跨域，解决跨域请求的一次残酷经历

首先&#xff0c;说一下我们的项目情况&#xff0c;我们项目中后端有一个过滤器&#xff0c;如果必须要登录的接口路径会被拦下来检查&#xff0c;前端要传一个token&#xff0c;然后后端根据这个token来判断redis中这个用户是否已经登录。 if (request.getMethod().equals(&qu…
阅读更多...
20、Python -- 变量作用域、局部函数

20、Python -- 变量作用域、局部函数

目录 变量作用域变量&#xff1f;字典&#xff1f;获取变量字典变量遮蔽解决方法&#xff1a;方法1&#xff1a;使用globals访问全局变量方法2&#xff1a;在函数中声明全局变量 局部函数封闭函数返回局部函数代码演示另一种写法 局部函数的遮蔽问题如图&#xff1a;解决方法&a…
阅读更多...
深入理解Java中的转义字符

深入理解Java中的转义字符

最近在学习《两周自制脚本语言》这本书&#xff0c;在词法分析的一些复杂的正则中用到了大量的转义字符’\&#xff0c;比如正则字符串中包含了这个部分\\\\\"你知道它是匹配什么的么&#xff1f; 反斜杠在字符串和正则表达式中都有特殊作用。今天让我们来深入理解一下Ja…
阅读更多...
如何使用drawio画流程图以及导入导出

如何使用drawio画流程图以及导入导出

画一个基本的流程图 你可以在线使用drawio, 或者drawon创建很多不同类型的图表。 如何使用编辑器&#xff0c;让我们以一个最基本的流程图开始。 流程图&#xff0c;就是让你可视化的描述一个过程或者系统。 图形和很少部分的文字表达就可以让读者很快的理解他们需要什么。 创…
阅读更多...
文心大模型走进高校！百度携手吉林大学计算机学院成功举办AI师资培训

文心大模型走进高校！百度携手吉林大学计算机学院成功举办AI师资培训

随着人工智能技术的快速发展&#xff0c;大模型已经成为了人工智能的主流发展方向&#xff0c;同时也对新时代AI人才的培养带来了新的思考与挑战。为了推动大模型及人工智能相关专业人员的培养&#xff0c;10月20日-22日&#xff0c;百度飞桨携手中国电子学会&#xff0c;吉林大…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023