8、电路综合-基于简化实频的SRFT微带线的带通滤波器设计
此处介绍微带线综合的巴特沃斯带通滤波器和切比雪夫带通滤波器的设计方法。对于理查德域的网络综合技术而言,这种带通综合和低通综合在本质上并无区别,因为理查德域函数是周期的。低通滤波器的SRFT微带线设计教程如下:
6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计
基于切比雪夫函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
7、电路综合-基于简化实频的SRFT微带线巴特沃兹低通滤波器设计
基于巴特沃斯函数进行电路综合,基于目标参数直接进行电路综合得到其对应的微带电路,给出了对应的理论与操作步骤(附Matlab代码)
如6、电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计中的巴特沃斯低通滤波器,其也是一个5-7GHz的带通滤波器:
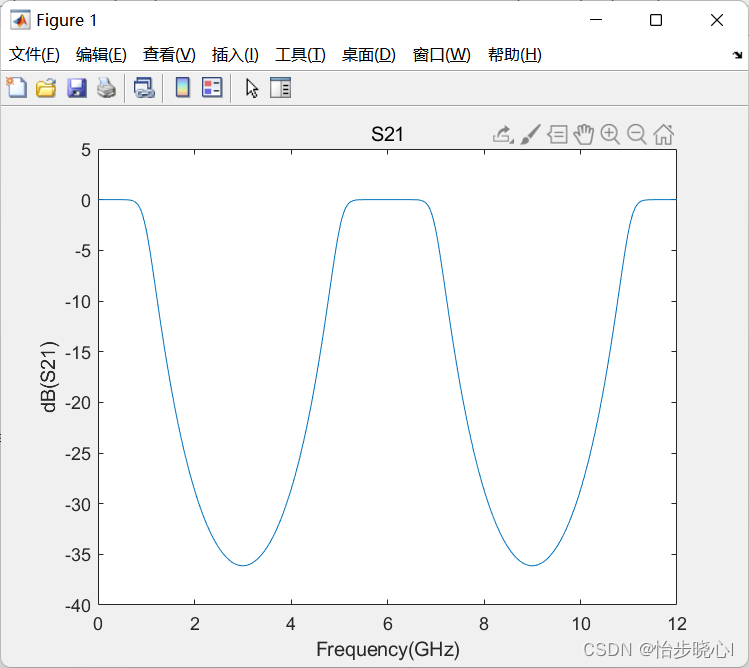
1、巴特沃斯带通滤波器设计
例如,此处我需要设计一个2-3GHz的带通滤波器,基本的理论公式是这样的(f1和f2是带通的通带范围,fc是转换成的低通的截止频率,fe是转换成的低通的阻带频率):
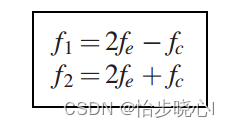
案例代码如下,具体代码参考最上面的链接:
clear
clc
close all
syms lamd
% 带通开始频率和截止频率
f1=2e9;
f2=3e9;
fc=(f2-f1)/2;
fe=(f1+f2)/4;
% %通带截止频率
% fc=1e9;
% %阻带频率
% fe=3e9;
wc=2*pi*fc;
we=2*pi*fe;
tau=pi/2/we;
% 滤波器阶数,必须为偶数
n=6;
%微带线电长度所在的频率
f=1e9;
%微带线电长度
ele_l=360*tau*f;
%求解频率范围,单位GHz
f_start=0.01;
f_stop=12;
f_step=0.01;
%光速
c=299792458;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度,单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);
%计算alpha
alpha=1.0/(sin(pi*wc/we/2));
G=simplify((1-lamd*lamd)^n+((-1)^n)*(alpha^(2*n))*lamd^(2*n));
G=double(coeffs(G,'all'));
G=G(1:2:end);
h=coeffs(((((-1)^(n)))^0.5*(alpha^(n))*lamd^(n)),'all');
h=double(h);
GX=paraconj(G);% Generate G(X) by setting X=-lambda^2
Xr=roots(GX);% Compute the roots og G(X)
z=sqrt(-Xr);% Compute the roots in lambda
%************************************************************
% Generation of g(lambda) from the given LHP roots
% Compute the first step k=1
n=length(z);
g=[1 z(1)];
for i=2:n
g=conv(g,[1 z(i)]);
end
Cnorm=sqrt(abs(G(1)));
g=Cnorm*real(g);
disp(['此处使用在',num2str(f/1e9),'GHz下电长度为',num2str(ele_l),'°的微带线进行实现']);
[z]=UE_sentez(h,g);
disp(['匹配使用的微带线的归一化特性阻抗为:',num2str(z(1:end-1))])
num_h=0;
for i=1:1:length(h)
num_h=num_h+h(i).*lamda.^(length(h)-i);
end
num_g=0;
for i=1:1:length(g)
num_g=num_g+g(i).*lamda.^(length(g)-i);
end
num_f=(1-lamda.^2).^(n/2);
figure
plot(freq_solve/1e9,20*log10(abs(num_f./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S21)')
title('S21')
figure
plot(freq_solve/1e9,20*log10(abs(num_h./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')
运行结果如下所示:
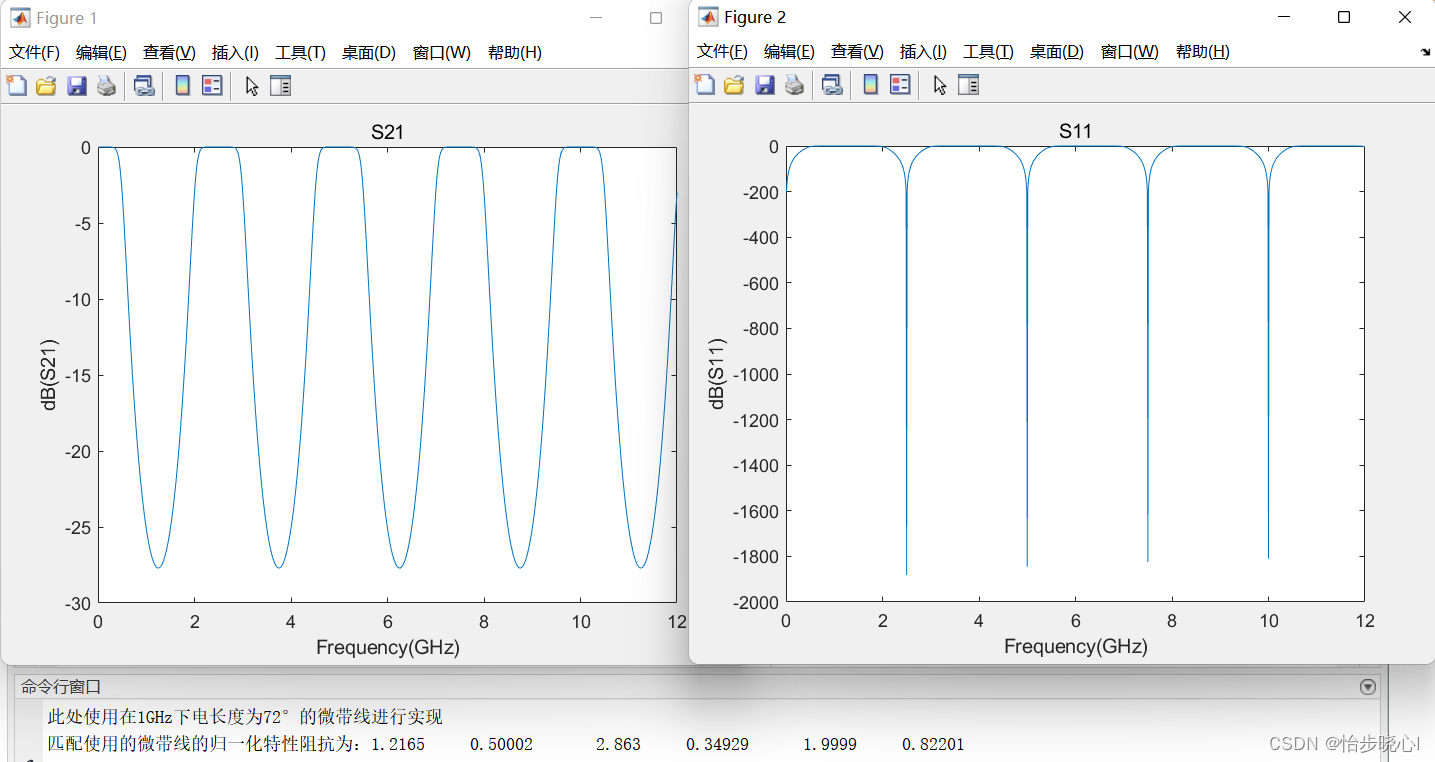
ADS构建仿真结构:
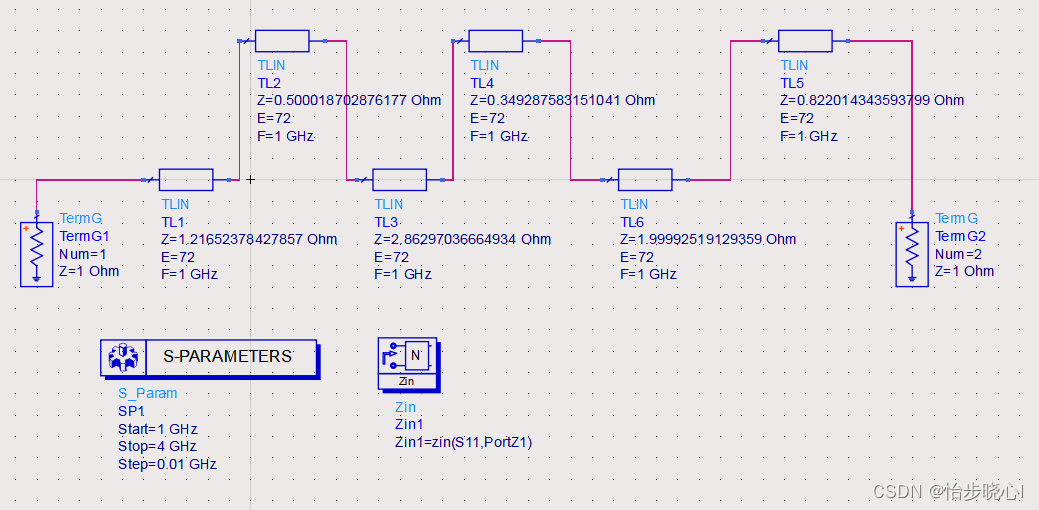
ADS仿真结果,完全一致:
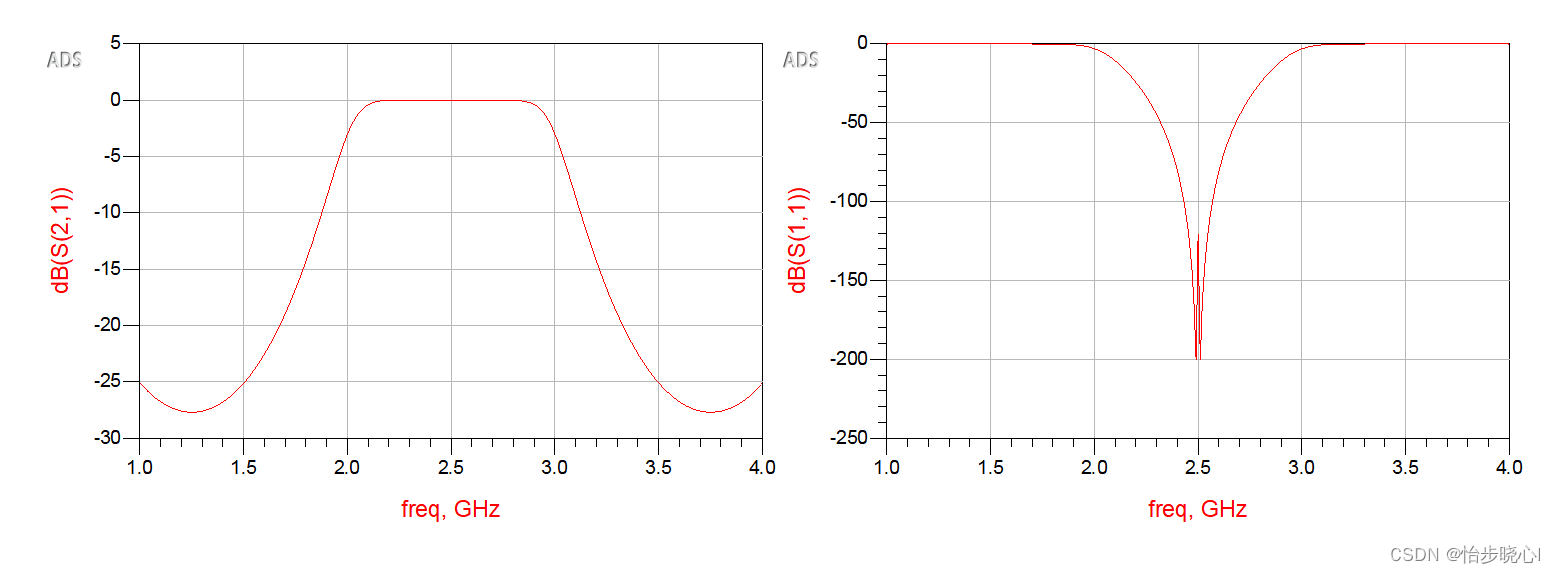
2、切比雪夫带通滤波器设计
例如,此处我需要设计一个2-3GHz的带通滤波器,基本的理论公式是这样的(f1和f2是带通的通带范围,fc是转换成的低通的截止频率,fe是转换成的低通的阻带频率):
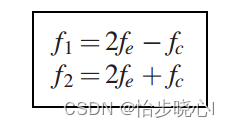
案例代码如下,具体代码参考最上面的链接:
clear
clc
close all
% 带通开始频率和截止频率
f1=2e9;
f2=3e9;
fc=(f2-f1)/2;
fe=(f1+f2)/4;
% %通带截止频率
% fc=1e9;
% %阻带频率
% fe=3e9;
%通带纹波,单位dB
ILR=0.4;
%阻带衰减,单位dB
IL=40;
% 计算纹波因子和角频率
eps_sq=10^(ILR/10)-1;
wc=2*pi*fc;
we=2*pi*fe;
% 计算传输延时tao
tau=pi/2/we;
% 计算alpha
alfa=1.0/(sin(pi*wc/we/2));
%计算所需的切比雪夫滤波器阶数
n=Cheby_Degree(IL,ILR,fc,fe);
%计算所需传输函数G和F
[F,G,g]=Denom_Cheby(n,eps_sq,alfa);
h =gtoh(F,G);
Z_imp=UE_sentez(h,g);
disp(['匹配使用的微带线的归一化特性阻抗为:',num2str(Z_imp(1:end-1))])
%使用在f Hz的电长度为ele_l的微带线进行实现
%光速
c=299792458;
%微带线电长度所在的频率
f=1e9;
%微带线电长度
ele_l=360*tau*f;
disp(['此处使用在',num2str(f/1e9),'GHz下电长度为',num2str(ele_l),'°的微带线进行实现']);
%求解频率范围,单位GHz
f_start=0.01;
f_stop=3;
f_step=0.01;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度,单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);
num_h=0;
for i=1:1:length(h)
num_h=num_h+h(i).*lamda.^(length(h)-i);
end
num_g=0;
for i=1:1:length(g)
num_g=num_g+g(i).*lamda.^(length(g)-i);
end
num_f=(1-lamda.^2).^(n/2);
figure
plot(freq_solve/1e9,20*log10(abs(num_f./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S21)')
title('S21')
figure
plot(freq_solve/1e9,20*log10(abs(num_h./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')
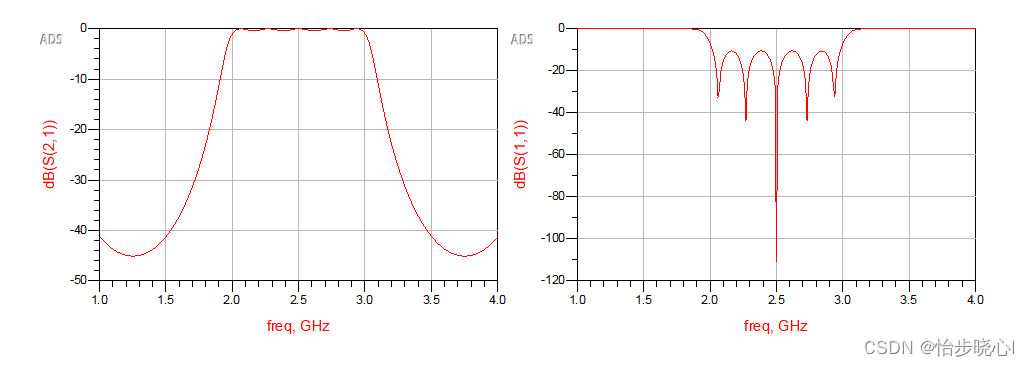
运行结果如下所示:
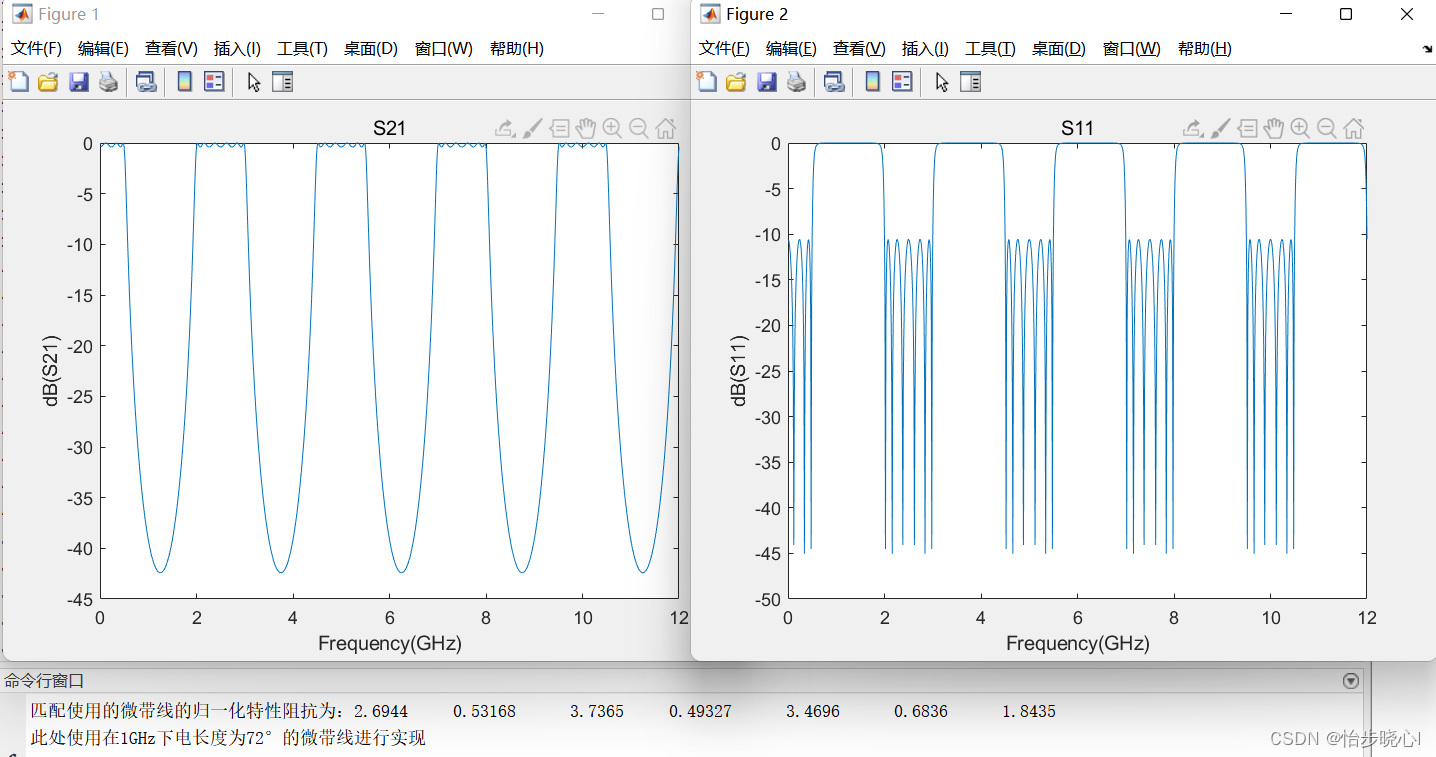
ADS构建仿真结构:
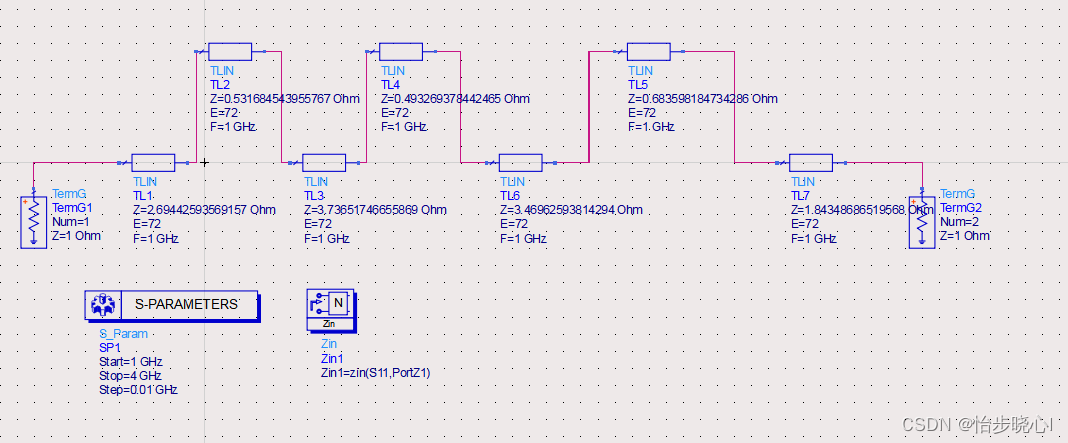
仿真结果展示: