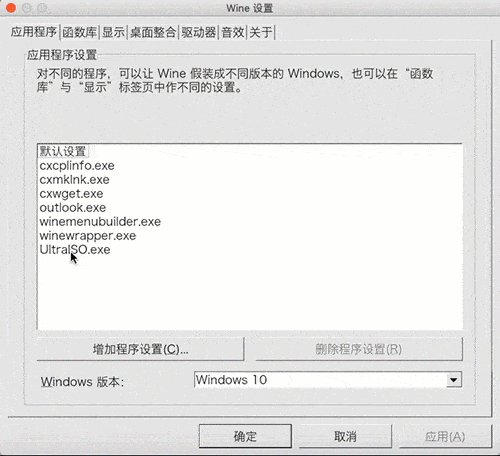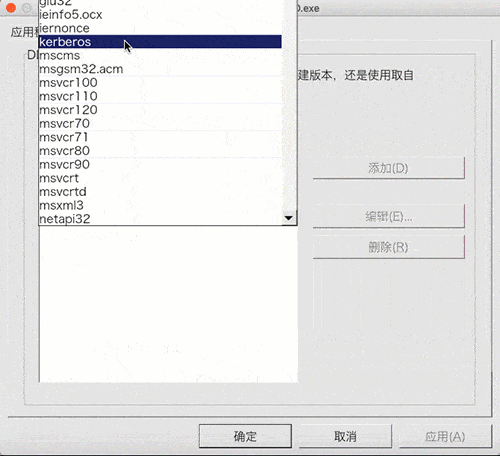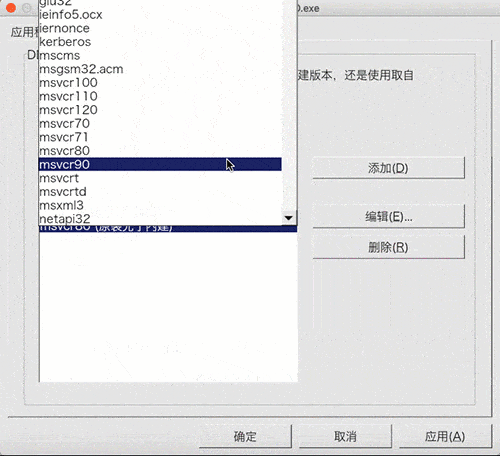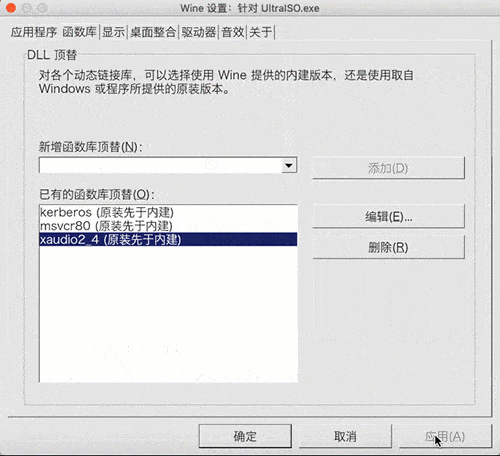
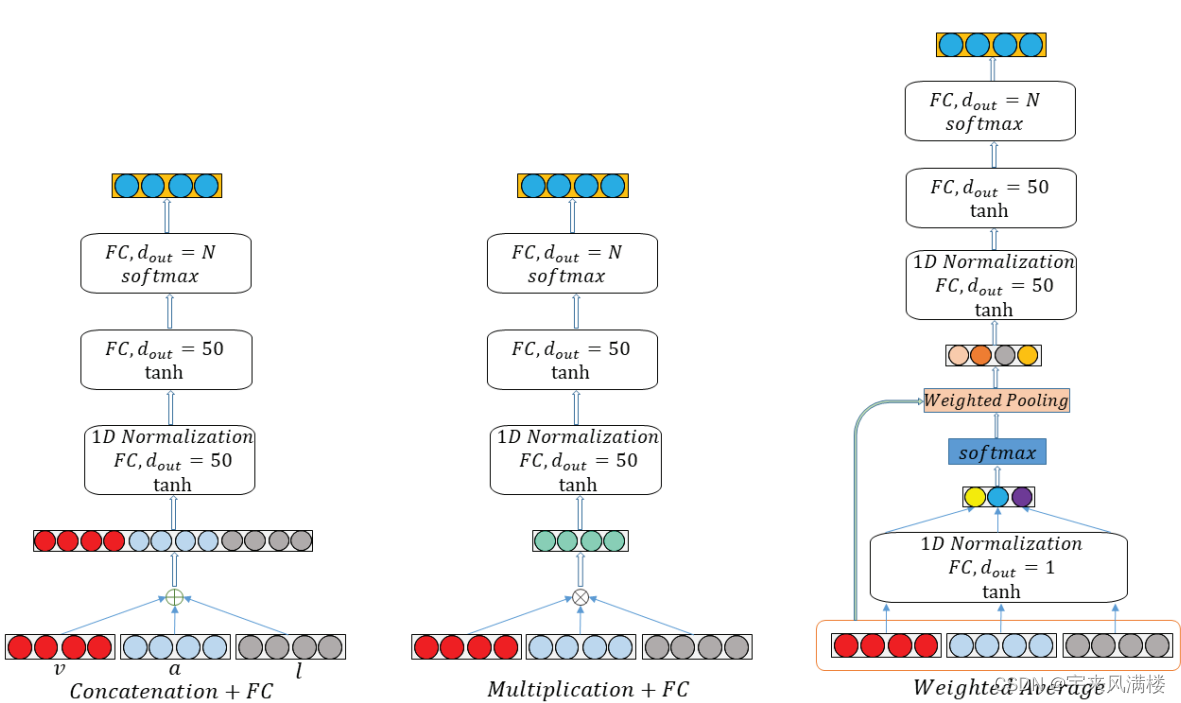
最近做一组测试,我复现了一组结果准备阐释另一个事。先看这个测试结果:

常规的一个 wrk2(expected_latency_timing 改为 actual_latency_timing 计数) 压 nginx 的测试,调整 -R 参数,Req/sec 同步增加,当 Req/sec 不再增加,nginx CPU 已 100%,处理饱和,在此之前 latency 几乎不变,在此之后,latency 剧烈增大。于是 Req/sec 开始不再增加的 R 值就是 “nginx 最优操作点”,在该点,Request 的处理具有最小时延,总吞吐最大。
可这是对 nginx 来说的,对 wrk,我是靠不断调 -R,肉眼观察找到这个 -R 值的,设它为 r。如果有 n 个互不可见的 wrk 在不同地方同时压 nginx,这个 r = r0 + r1 + … rn 将怎样在所有 wrk 间分配,每一个 wrk 实例有办法找到自己的 r_i 吗?如何确保 r 的分配对所有 wrk 实例是公平的? 这个问题的解就是 bbr 问题的解。
看一个更现实的例子。
如何判定找到一家好吃的饭店?很多人说看哪家饭店排队多。但这是非常矛盾的,为了一口好吃的,难道非要付出排队的代价吗?如果大家都想吃好吃的却又都不想排队,有没有什么办法找到一家不用排队,但大堂里只剩下一个位置的饭店呢?
事实上满座率 = 100%,等待率 = 0 的饭店才是最好的饭店。但更为现实的场景是,几乎所有饭店,要么外面排着等待就餐的长队,要么里面服务员比顾客人多,几千年人们都没有办法找到工作在 “最佳操作点” 的饭店。
把范围缩小到公司食堂范围,即使经理已经给出了针对不同部门的不同 “建议就餐时间”,当某个特定的人去吃饭时依然会看到有些档口排着长队,有些档口门可罗雀。除非经理为每个特定个人安排特定就餐时间,但这会增加经理成本,人员稍有变动就要重新来一遍,如此成本加持,“最佳操作点” 就不再最佳了。
除非你知道其它所有人的策略,否则对于单独个人,如果找不到 “最佳操作点”,不如说它根本不存在。
bbr 基于单流测速的一厢情愿方案注定只是一意孤行,在现实中各个领域,人们到处都在试图解决相同的问题,人们试图在统计的世界中寻找精确的解,但几千年都没找到。
人们憧憬 “刚刚好”,但现实给予的要么太多,要么不够。
很难找到一辆只剩下一个座位的公交车,如果你找到了并且坐到了那个仅剩的位置,下一个上来的就大概率要站着了,如果到达某站点,可能一下下去很多人,留出很多空位而不是恰好一个。
不存在 “刚刚好” 的期望会导致人们很多误判,而误判的结果具有累积效果,这种积累效果反过来让现实越发偏离 “刚刚好” 的期望,如此滚雪球一般。
形成判断要基于数据,凡是基于数据的分析都要承担滞后性风险,风险的累积性来自于单向时间,1 + 1 = 2,却不允许减法将 2 消除,只能靠除法将它稀释,在很久之后 2 / 10000000 约等于 0。要么过多,要么不够,不能将 “未来的过多” 沿着时间轴往前搬,以弥补 “现在的不够”,现在过多,万一未来也过多,就累积了,大致就这么解释。时间的单向是统计突发的根源。
最近关于时间借贷的想法亦来自于此,《利息原理》恰恰给出并深入分析了一个实际例子。
按照单向时间分析,结论很明显,如果网络提供了 buffer 用以吸收统计突发,只能将 “当前的过多” 沿时间轴向后搬,以弥补 “未来的不足”,在不可预测的未来同样过多时,buffer 则堆积,buffer 的大小影响的只是堆积程度。换句话说,buffer 倾向于 “总是会被填满”。
观察自然界,持续大流量河流附近特别是汇集处,非常容易形成湖泊,大自然是时间不耐。bbr 的问题等同于下面的描述。一条大河上有座大坝,如何才能让大坝不蓄水,就好像没有这座大坝一样,答案很简单,把大坝拆了,因为本来就没有这座大坝。如果在大坝上游再引入一条河注入,让大坝不蓄水就很难。为什么非要让大坝不蓄水呢,大坝本身的蓄水就是对枯水期的借贷,一种常平仓而已。bbr 对 buffer 的纠结等同于让大坝不蓄水。
展示一下问题:
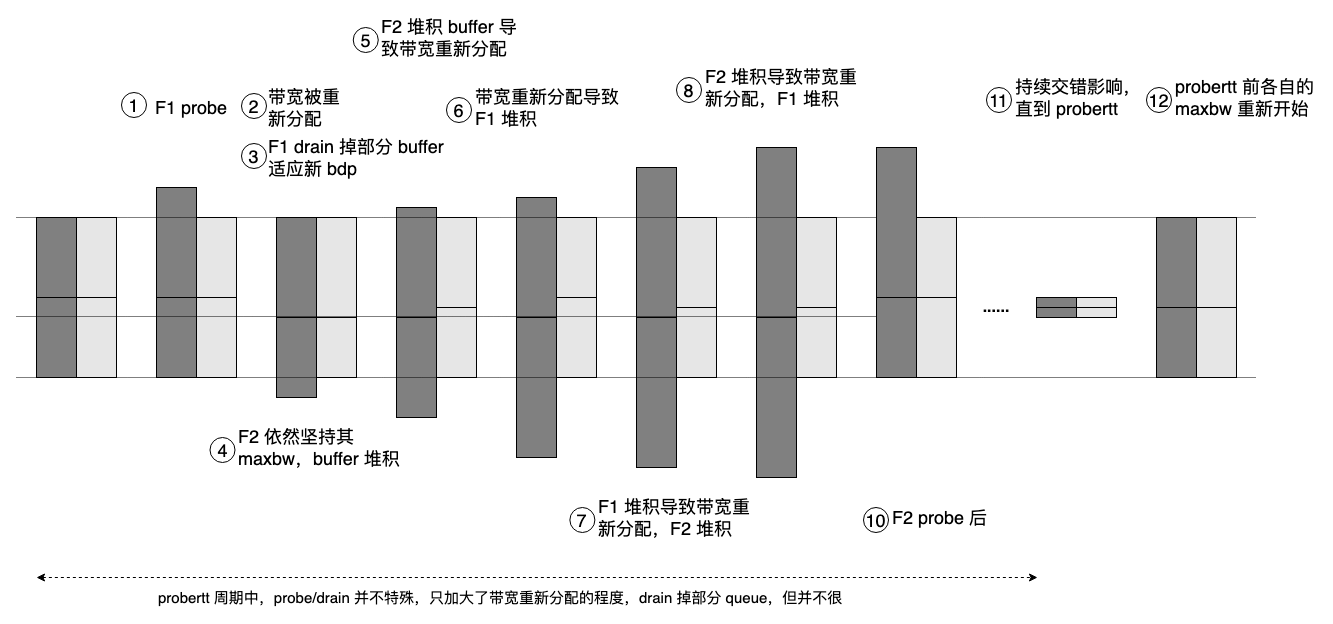
多流 bbr 的流程必须围绕 buffer 展开,10 rounds or 更小的 N rounds 周期并不改变围绕 buffer 展开的本质。 事实上当 deliver_rate < gain * pacing_rate 就足以说明发生了 buffer 挤占(时间借贷),要彻底 drain,而不仅仅归还 5 / 4 * old_maxbw * min_rtt - new_maxbw * min_rtt,此时的 new_maxbw 是 buffer 作用下带宽重新分配的结果而不是空闲带宽。
bbr 的基本假设在事实上根本不存在。
前面餐厅的例子有个附加条件,好吃的餐厅才会排队,事实上这个条件完全可以去掉,任何统计复用系统,只要它将要满载,那么排队就是必然的,对于独立排队实体而言,该排队是不可预测和不可分析的(但对服务台却可以预测和分析),即使不基于排队论分析,从单向时间也能自然推导出这一结论。
还是相同的论点,包括 bbr (作为统计复用实体)在内的端到端 cc 对系统状态的预判存在上限,该上限距离理论 “最优操作点” 甚远。无论怎么做都抓不到它,当你压缩 persist 度,规模也缩小了,当你放大它,却又模糊了。
皮鞋没有蹬上,露着白袜子。
浙江温州皮鞋湿,下雨进水不会胖。