【torch高级】一种新型的概率学语言pyro（01/2）

一、说明

贝叶斯推理，也就是变分概率模型估计，属于高级概率学模型，极有学习价值；一般来说，配合实际活动学习可能更直观，而pyro是pytorch的概率工具，不同于以往的概率工具，只是集中于统计工具，而pyro具备贝叶斯推断的全套设计，因此，跟着pyro学习会更有前景，因此，建议读者重视pyro的存在，这就是本文的意义所在。

二、火焰兵简介

2.1 火焰是个啥

概率是在不确定性下进行推理的数学，就像微积分是对变化率进行推理的数学一样。它为理解现代机器学习和人工智能的大部分内容提供了一个统一的理论框架：用概率语言构建的模型可以捕获复杂的推理，知道他们不知道什么，并在没有监督的情况下揭示数据结构。

直接指定概率模型可能很麻烦，而且实现它们也很容易出错。概率编程语言 (PPL) 通过将概率与编程语言的表示能力相结合来解决这些问题。概率程序是普通确定性计算和代表数据生成过程的随机采样值的混合。

通过观察概率程序的结果，我们可以描述一个推理问题，大致翻译为：“如果这个随机选择具有某个观察值，那么什么一定是真的？” PPL 明确强制分离已经隐含在概率数学中的模型规范、要回答的查询和计算答案的算法之间的关注点分离。

Pyro 是一种基于 Python 和 PyTorch 构建的概率编程语言。Pyro 程序只是 Python 程序，而其主要推理技术是随机变分推理，它将抽象的概率计算转换为 PyTorch 中通过随机梯度下降解决的具体优化问题，使概率方法适用于以前难以处理的模型和数据集大小。

在本教程中，我们将简要介绍概率机器学习和 Pyro 概率编程的基本概念。我们通过涉及线性回归的示例数据分析问题来实现这一点，线性回归是机器学习中最常见和基本的任务之一。我们将了解如何使用 Pyro 的建模语言和推理算法将不确定性纳入回归系数的估计中。

2.2 在python中安装pyro

2.2.1 安装的步骤分三个过程：

1）步骤1
 pip3 install pyro-ppl 

2）步骤2

git clone https://github.com/pyro-ppl/pyro.git

3）步骤3

cd pyro
pip install .[extras]

2.2.2 安装过程的错误和改出

执行：git clone https://github.com/pyro-ppl/pyro.git

可能的错误是：

OpenSSL SSL_read: Connection was reset, errno 10054

此为验证过程出错，可以从下列操作改出：

git config --global http.sslVerify "false"

执行：git clone https://github.com/pyro-ppl/pyro.git

可能的错误是：

Failed to connect to github.com port 443: Timed out

此为验证过程出错，可以从下列操作改出：

git config --global http.proxy http://127.0.0.1:1080
git config --global https.proxy http://127.0.0.1:1080

git config --global --unset http.proxy
git config --global --unset https.proxy

执行：git clone https://github.com/pyro-ppl/pyro.git

执行成功，等待下载完成；完成下载后安装：

3）步骤3

cd pyro
pip install .[extras]

三、大纲提示

介绍
大纲
设置
背景：概率机器学习
- 背景：概率模型
- 背景：推理、学习和评估
示例：地理和国民收入
Pyro 中的模型
- 模型示例：最大似然线性回归
- 背景：pyro.sample 原语
- 背景：pyro.param 原语
- 背景：pyro.plate 原语
- 示例：从最大似然回归到贝叶斯回归
Pyro 中的推理
- 背景：变分推理
- 背景：“引导”程序作为灵活的近似后验
- 示例：Pyro 中贝叶斯线性回归的平均场变分近似
- 背景：估计和优化证据下限 (ELBO)
- 示例：通过随机变分推理 (SVI) 的贝叶斯回归
Pyro 中的模型评估
- 背景：使用后验预测检查的贝叶斯模型评估
- 示例：Pyro 中的后验预测不确定性
- 示例：使用满秩指南重新审视贝叶斯回归
下一步

四、设置

让我们首先导入我们需要的模块。

%reset -s -f
import logging
import os

import torch
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

import pyro

[43]:

smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('1.8.6')

pyro.enable_validation(True)
pyro.set_rng_seed(1)
logging.basicConfig(format='%(message)s', level=logging.INFO)

# Set matplotlib settings
%matplotlib inline
plt.style.use('default')

五、背景：概率机器学习

大多数数据分析问题可以理解为对三个基本高级问题的阐述：

在观察任何数据之前我们对问题了解多少？
根据我们的先验知识，我们可以从数据中得出什么结论？
这些结论有意义吗？

在数据科学和机器学习的概率或贝叶斯方法中，我们用概率分布的数学运算形式化这些方法。

5.1 背景：概率模型

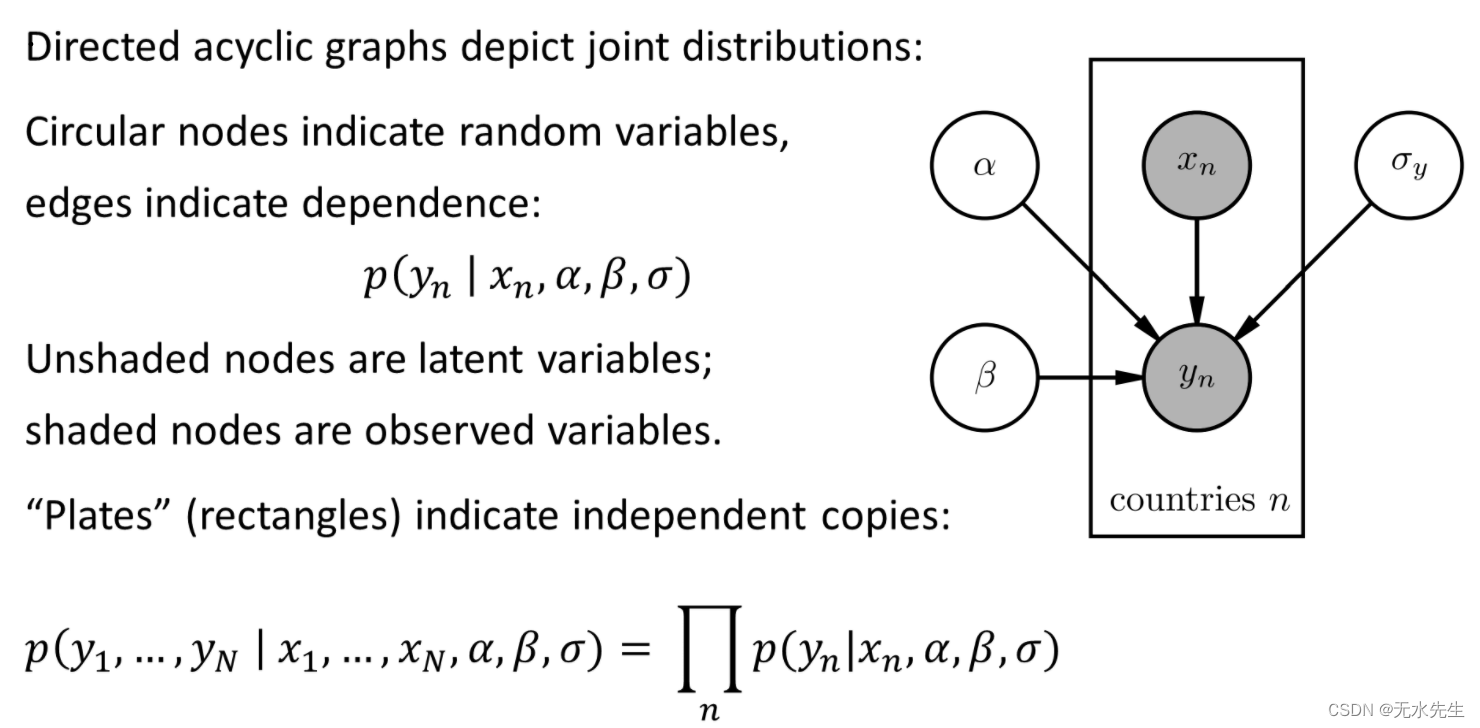
首先，我们以概率模型或随机变量集合的联合概率分布的形式表达我们所知道的关于问题中的变量以及它们之间的关系的所有信息。模型有观察结果x和潜在随机变量z以及参数θ。它通常具有以下形式的联合密度函数

$p_{\theta}({\bf x}, {\bf z}) = p_{\theta}({\bf x}|{\bf z}) p_{\theta}({\bf z})$

潜在变量的分布 $p_{\theta}({\bf z})$ 在这个公式中称为先验，以及给定潜在变量的观察变量的分布 $p_{\theta}({\bf x}|{\bf z})$ 称为可能性。

我们通常要求各种条件概率分布 $p_i$ 组成一个模型 $p_{\theta}({\bf x}, {\bf z})$ 具有以下属性（通常由Pyro和PyTorch Distributions中可用的分布满足）：

我们可以有效地从每个 $p_i$
我们可以有效地计算逐点概率密度 $p_i$
$p_i$ 对于参数是可微分的θ

概率模型通常以用于可视化和通信的标准图形表示法来描述，总结如下，尽管 Pyro 中可以表示没有固定图形结构的模型。在具有大量重复的模型中，使用板表示法很方便，之所以这么称呼是因为它以图形方式显示为围绕变量的矩形“板”，以指示内部随机变量的多个独立副本。

5.2 背景：推理、学习和评估

一旦我们指定了一个模型，贝叶斯规则就会告诉我们如何使用它来执行推理，或者通过计算后验分布从数据中得出有关潜在变量的结论z:

$p_{\theta}({\bf z} | {\bf x}) = \frac{p_{\theta}({\bf x} , {\bf z})}{ \int \! d{\bf z}\; p_{\theta}({\bf x} , {\bf z}) }$

为了检查建模和推理的结果，我们想知道模型与观测数据的拟合程度如何x，我们可以用证据或边际可能性来量化

$p_{\theta}({\bf x}) = \int \! d{\bf z}\; p_{\theta}({\bf x} , {\bf z})$

还可以对新数据进行预测，我们可以使用后验预测分布来进行预测

$p_{\theta}(x' | {\bf x}) = \int \! d{\bf z}\; p_{\theta}(x' | {\bf z}) p_{\theta}({\bf z} | {\bf x})$

最后，通常需要学习参数θ我们的模型来自观察到的数据x，我们可以通过最大化边际似然来实现：

$\theta_{\rm{max}} = \rm{argmax}_\theta p_{\theta}({\bf x}) = \rm{argmax}_\theta \int \! d{\bf z}\; p_{\theta}({\bf x} , {\bf z})$

5.3 示例：地理和国民收入

下示例改编自 Richard McElreath 撰写的优秀著作《统计反思》的第 7章，鼓励读者阅读该书，以获取对贝叶斯数据分析更广泛实践的简单介绍（所有章节的 Pyro 代码均可用）。

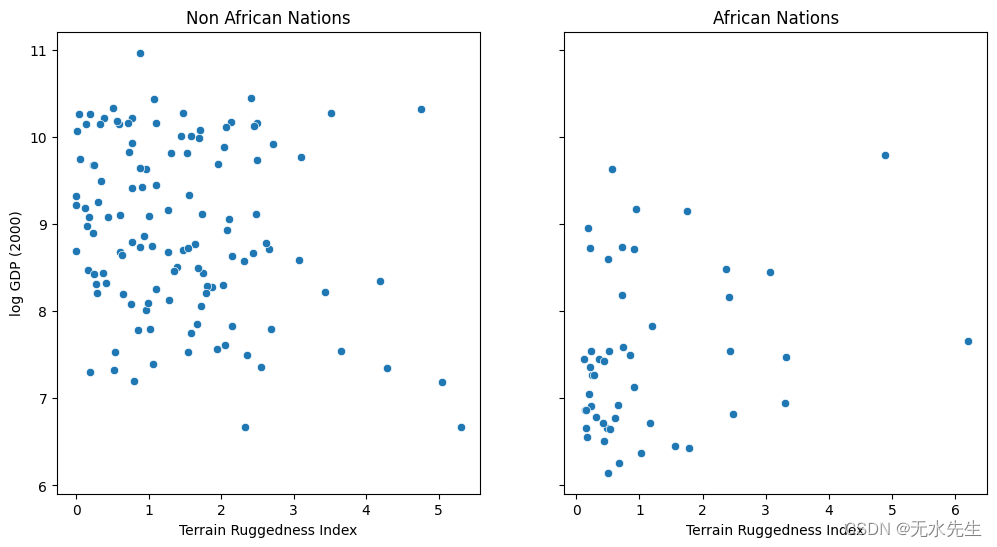
我们想探讨一个国家的地形异质性（通过地形崎岖指数（数据集中的变量崎岖度）衡量）与其人均 GDP 之间的关系。特别是，原论文（《崎岖：非洲恶劣地理的祝福》）的作者指出，地形崎岖或恶劣的地理与非洲以外地区较差的经济表现有关，但崎岖的地形却产生了相反的影响关于非洲国家的收入。

让我们看一下数据并研究这种关系。我们将重点关注数据集中的三个特征：

rugged：量化地形坚固性指数；
cont_africa：指定国家是否在非洲；
rgdppc_2000：2000年人均实际GDP；

[44]:

DATA_URL = "https://d2hg8soec8ck9v.cloudfront.net/datasets/rugged_data.csv"
data = pd.read_csv(DATA_URL, encoding="ISO-8859-1")
df = data[["cont_africa", "rugged", "rgdppc_2000"]]

响应变量 GDP 高度偏斜，因此我们将在继续之前对其进行对数转换。

[45]:

df = df[np.isfinite(df.rgdppc_2000)]
df["rgdppc_2000"] = np.log(df["rgdppc_2000"])

然后，我们将此数据帧后面的 Numpy 数组转换为torch.Tensor用于使用 PyTorch 和 Pyro 进行分析的数组。

[46]:

train = torch.tensor(df.values, dtype=torch.float)
is_cont_africa, ruggedness, log_gdp = train[:, 0], train[:, 1], train[:, 2]

数据可视化表明，坚固性和 GDP 之间确实可能存在某种关系，但需要进一步分析来证实这一关系。我们将了解如何在 Pyro 中通过贝叶斯线性回归来做到这一点。

[47]:

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
african_nations = df[df["cont_africa"] == 1]
non_african_nations = df[df["cont_africa"] == 0]
sns.scatterplot(x=non_african_nations["rugged"],
                y=non_african_nations["rgdppc_2000"],
                ax=ax[0])
ax[0].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="Non African Nations")
sns.scatterplot(x=african_nations["rugged"],
                y=african_nations["rgdppc_2000"],
                ax=ax[1])
ax[1].set(xlabel="Terrain Ruggedness Index",
          ylabel="log GDP (2000)",
          title="African Nations");

六、Pyro 中的模型

Pyro 中的概率模型被指定为 Python 函数，这些函数使用特殊的原始函数从潜在变量生成观察到的数据，这些函数的行为可以通过 Pyro 的内部结构根据正在执行的高级计算进行更改。model(*args, **kwargs)

具体来说，不同的数学部分model()通过映射进行编码：

潜在随机变量 $z\Leftrightarrow pyro.sample$ （见网页）
观察到的随机变量 $x\Leftrightarrow pyro.sample$ 带有obs关键字参数的pyro.sample
可学习参数 $\theta \Longleftrightarrow pyro.sample$
盘子⟺ Pyro.plate上下文管理器

我们在下面的第一个线性回归 Pyro 模型的背景下详细研究了这些组件中的每一个。

6.1 模型示例：最大似然线性回归

如果我们写出线性回归预测器的公式 $\beta X + \alpha$ 作为 Python 表达式，我们得到以下结果：

mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness

为了将其构建为数据集的完整概率模型，我们需要制作回归系数 $\alpha$ 和 $\beta$ 可学习的参数并在预测平均值周围添加观察噪声。我们可以使用上面介绍的 Pyro 原语来表达这一点，并使用Pyro.render_model()可视化结果模型：

[48]:

import pyro.distributions as dist
import pyro.distributions.constraints as constraints

def simple_model(is_cont_africa, ruggedness, log_gdp=None):
    a = pyro.param("a", lambda: torch.randn(()))
    b_a = pyro.param("bA", lambda: torch.randn(()))
    b_r = pyro.param("bR", lambda: torch.randn(()))
    b_ar = pyro.param("bAR", lambda: torch.randn(()))
    sigma = pyro.param("sigma", lambda: torch.ones(()), constraint=constraints.positive)

    mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness

    with pyro.plate("data", len(ruggedness)):
        return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

pyro.render_model(simple_model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True)

[48]:

上图未显示模型参数a、b_a、b_r、b_ar和sigma。我们可以设置render_params=True渲染模型参数。

[49]:

pyro.render_model(simple_model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True, render_params=True)

[49]:

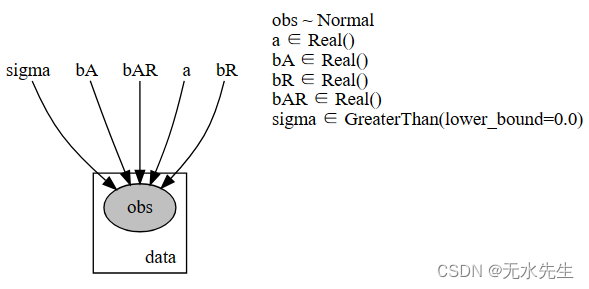
该参数将显示对参数的约束。例如，是一个标准差，应该是非负的。因此，其约束表示为“sigmarender_distributions = Truesigma∈大于（lower_bound=0.0）”。

学习的参数simple_model将构成最大似然估计并产生回归系数的点估计。然而，在这个例子中，我们的数据可视化表明我们不应该对回归系数的任何单个值过于自信。相比之下，完全贝叶斯方法将产生对不同可能参数值以及模型预测的不确定性估计。

在制作线性模型的贝叶斯版本之前，让我们停下来仔细看看第一段 Pyro 代码。

6.2 背景：`pyro.sample`原始

Pyro 中的概率程序是围绕原始概率分布的样本构建的，标记为pyro.sample：

def sample(
    name: str,
    fn: pyro.distributions.Distribution,
    *,
    obs: typing.Optional[torch.Tensor] = None,
    infer: typing.Optional[dict] = None
) -> torch.Tensor:
    ...

在我们上面的模型中simple_model，该行

return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

可以表示潜在变量或观察变量，具体取决于是否simple_model给定log_gdp值。当log_gdp未提供并且"obs"是潜在的时，它相当于（pyro.plate通过假设暂时忽略上下文）调用分发的底层方法：len(ruggedness) == 1.sample

return dist.Normal(mean, sigma).sample()

这种解释是偶尔将 Pyro 程序引用为随机函数的背后原因，随机函数是 Pyro 的一些旧文档中使用的一个相当晦涩的术语。

当simple_model给出一个log_gdp参数并被"obs"观察时，该pyro.sample语句

return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

总会返回log_gdp：

return log_gdp

但是，请注意，当观察到任何样本语句时，模型中每个其他样本语句的累积效应都会按照贝叶斯规则发生变化；Pyro推理算法的工作是“向后运行程序”并为pyro.sample模型中的所有语句分配数学上一致的值。

此时要问的一个合理的问题是为什么pyro.sample和其他基元必须有名称。用户和 Pyro 内部人员利用名称来区分模型、观察和推理算法的规范，这是概率编程语言的一个关键卖点。要查看这样的示例，我们可以查看高阶原始的pyro.condition，它解决了针对单个 Pyro 模型编写许多查询的问题：

def condition(
    model: Callable[..., T],
    data: Dict[str, torch.Tensor]
) -> Callable[..., T]:
    ...

pyro.condition接受一个模型和一个（可能是空的）字典，将名称映射到观察值，并将每个观察传递到pyro.sample其名称指示的语句。在我们的示例中simple_model，我们可以删除log_gdp作为参数并用更简单的接口替换它。

def simpler_model(is_cont_africa, ruggedness): ...

conditioned_model = pyro.condition(simpler_model, data={"obs": log_gdp})

其中conditioned_model相当于

conditioned_model = functools.partial(simple_model, log_gdp=log_gdp)

6.3 背景：`pyro.param`原始

我们模型中使用的下一个原语是pyro.param，它是一个用于读取和写入 Pyro 的键值参数存储的前端：

def param(
    name: str,
    init: Optional[Union[torch.Tensor, Callable[..., torch.Tensor]]] = None,
    *,
    constraint: torch.distributions.constraints.Constraint = constraints.real
) -> torch.Tensor:
    ...

就像pyro.sample,pyro.param总是以名称作为第一个参数来调用。第一次pyro.param使用特定名称调用时，它将第二个参数指定的初始值存储init在参数存储中，然后返回该值。之后，当使用该名称调用它时，它会从参数存储中返回值，而不管任何其他参数如何。参数初始化后，不再需要指定init检索其值（例如 pyro.param("a")）。

第二个参数init可以是一个torch.Tensor或一个不带参数并返回张量的函数。第二种形式很有用，因为它避免了重复构造仅在模型第一次运行时使用的初始值。

与 PyTorch 不同torch.nn.Parameter，Pyro 中的参数可以显式约束为各种子集 $\mathbb{R}^n$ ，这是一个重要的特征，因为许多基本概率分布的参数具有受限的域。例如，分布scale的参数Normal必须为正。pyro.param,的可选第三个参数constraint是初始化参数时存储的 torch.distributions.constraints.Constraint对象；每次更新后都会重新应用约束。Pyro 附带了大量预定义的约束。

pyro.param值在模型调用中持续存在，除非参数存储由优化算法更新或通过pyro.clear_param_store()清除。与不同的是pyro.sample，pyro.param可以在模型中多次调用相同的名称；每个具有相同名称的调用都会返回相同的值。全局参数存储本身可以通过调用 pyro.get_param_store()来访问。

在我们上面的模型中simple_model，语句

a = pyro.param("a", lambda: torch.randn(()))

在概念上与下面的代码类似，但具有一些附加的跟踪、序列化和约束管理功能。

simple_param_store = {}
...
def simple_model():
    a_init = lambda: torch.randn(())
    a = simple_param_store["a"] if "a" in simple_param_store else a_init()
    ...

虽然本介绍性教程用pyro.param于参数管理，但 Pyro 还通过pyro.nn.PyroModule与 PyTorch 熟悉的API, torch.nn.Module兼容。

6.4 背景：`pyro.plate`原始

pyro.plate是 Pyro 的板表示法的形式编码，广泛用于概率机器学习，以简化具有大量条件独立且同分布随机变量的模型的可视化和分析。

def plate(
    name: str,
    size: int,
    *,
    dim: Optional[int] = None,
    **other_kwargs
) -> contextlib.AbstractContextManager:
    ...

从概念上讲，pyro.plate语句相当于for循环。在中simple_model，我们可以替换这些行

with pyro.plate("data", len(ruggedness)):
    return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

使用 Pythonfor循环

result = torch.empty_like(ruggedness)
for i in range(len(ruggedness)):
    result[i] = pyro.sample(f"obs_{i}", dist.Normal(mean, sigma), obs=log_gdp[i] if log_gdp is not None else None)
return result

当重复变量的数量（len(ruggedness)在本例中）很大时，使用 Python 循环会非常慢。由于循环中的每次迭代都独立于其他迭代，因此pyro.plate使用 PyTorch 的数组广播在单个向量化操作中并行执行迭代，如以下等效向量化代码所示：

mean = mean.unsqueeze(-1).expand((len(ruggedness),))
sigma = sigma.unsqueeze(-1).expand((len(ruggedness),))
return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

实际上，在编写 Pyro 程序时，pyro.plate作为矢量化工具最有用。然而，正如SVI 教程第 2 部分中所述，它对于管理数据子采样以及作为某些变量是独立的推断算法的信号也很有用。

6.5 示例：从最大似然回归到贝叶斯回归

为了建立贝叶斯线性回归模型，我们需要指定参数的先验分布 $\alpha \in \mathbb{R}$ 和 $\beta \in \mathbb{R}^3$ （此处扩展为标量b_a、b_r和b_ar）。这些是概率分布，代表我们在观察有关合理值的任何数据之前的信念α和β。我们还将添加一个随机比例参数σ控制观察噪声。

在 Pyro 中表达线性回归的贝叶斯模型非常直观：我们只需将每个语句替换pyro.param为pyro.sample配备有描述每个参数的先验信念的Pyro Distribution 对象的语句。

对于常数项α，我们使用具有较大标准差的正态先验来表明我们相对缺乏关于基线 GDP 的先验知识。对于其他回归系数，我们使用标准正态先验（以 0 为中心）来表示我们缺乏关于协变量与 GDP 之间的关系是正还是负的先验知识。对于观测噪声σ，我们使用低于 0 的平坦先验，因为该值必须为正才能成为有效的标准差。

[50]:

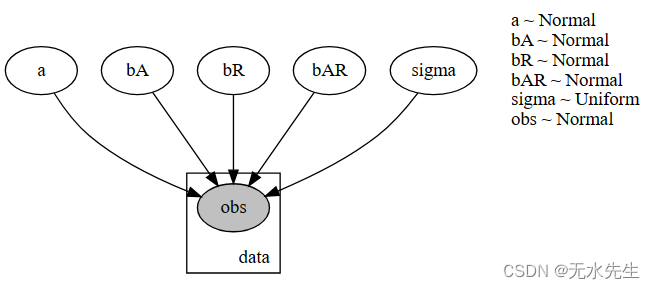
def model(is_cont_africa, ruggedness, log_gdp=None):
    a = pyro.sample("a", dist.Normal(0., 10.))
    b_a = pyro.sample("bA", dist.Normal(0., 1.))
    b_r = pyro.sample("bR", dist.Normal(0., 1.))
    b_ar = pyro.sample("bAR", dist.Normal(0., 1.))
    sigma = pyro.sample("sigma", dist.Uniform(0., 10.))

    mean = a + b_a * is_cont_africa + b_r * ruggedness + b_ar * is_cont_africa * ruggedness

    with pyro.plate("data", len(ruggedness)):
        return pyro.sample("obs", dist.Normal(mean, sigma), obs=log_gdp)

pyro.render_model(model, model_args=(is_cont_africa, ruggedness, log_gdp), render_distributions=True)