分布估计算法（Estimation of distribution algorithm，EDA）

概论

分布估计算法（Estimation of distribution algorithm，EDA）是一种新兴的基于统计学原理的随机优化算法。

为什么要叫这个名字呢？

首先，“分布”指的就是概率分布。

其次，“估计”指的是这个概率分布是我们根据数据以及算法的迭代过程中估算出来的，是一个近似，并不是真实的分布。

但是大数定律告诉我们，样本足够大的情况下，样本出现频率会无限接近于真实概率。因此，这种估计的方法是具有一定的理论依据的。

EDA v.s. GA

其实这两个算法整体思路非常相似。

不同的是，GA通过交叉、变异产生新解，EDA则通过估计截至目前，群体中最优解的概率分布（即较优个体主要都分布在哪一区间），这样做的好处是，可以使得搜索具有一定的方向性。

两种算法的流程图如下：

在这里插入图片描述

图1：遗传算法的流程图

在这里插入图片描述

图2：分布估计算法的流程图

算法原理

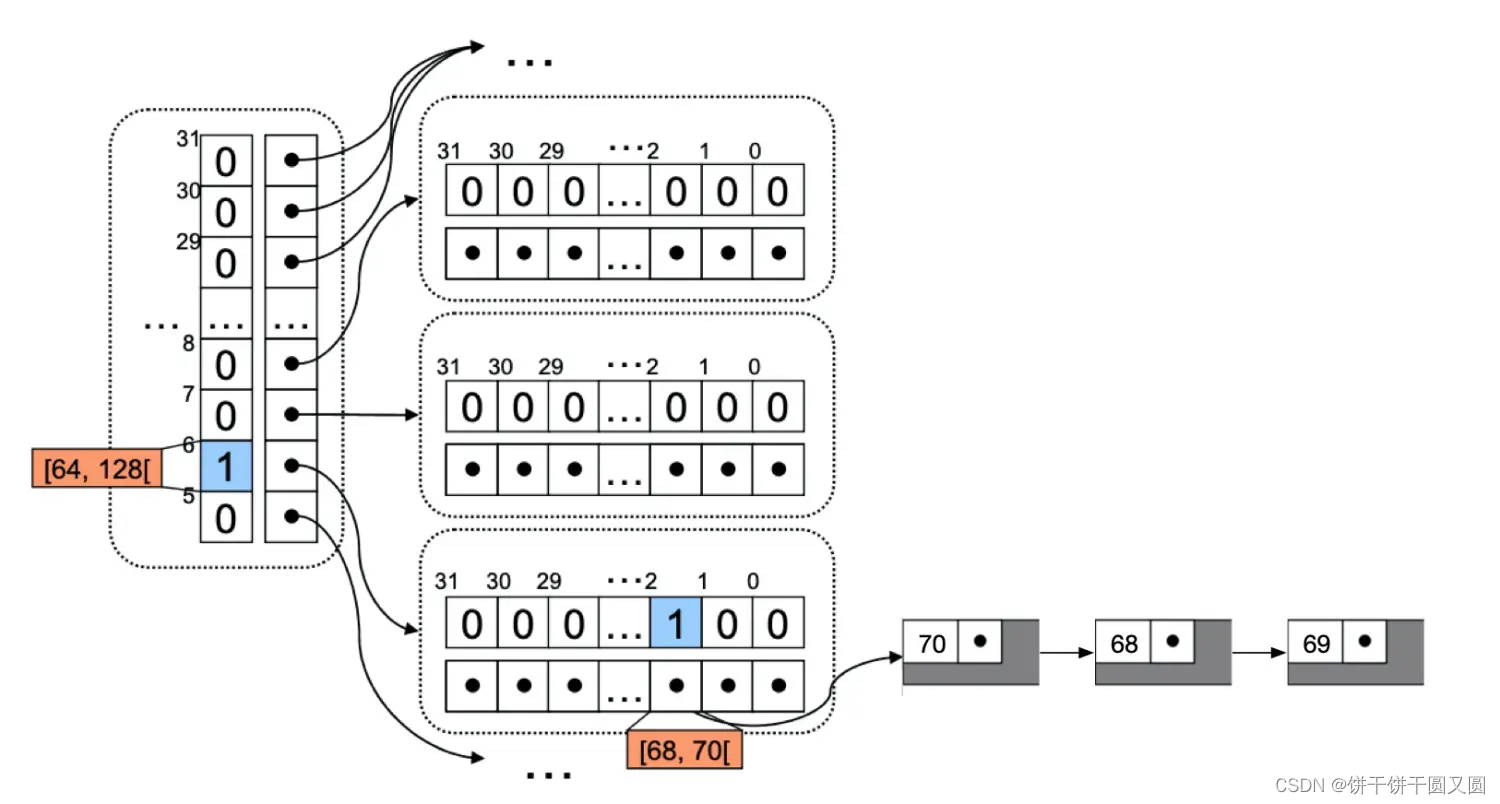
概率模型是EDA的核心, EDA通过概率模型及其更新来描述解空间分布以及种群整体进化趋势. 按概率模型的结构及变量间的相互关系, 可分为变量无关、双变量相关和多变量相关 EDA。¹

上面已经提到，分布估计算法与遗传算法非常相似，关于选择过程可以参考这篇文章：遗传算法（附简单案例及matlab详细代码），因此不再介绍其相同的流程，只介绍不同点。

EDA算法是一个大类的算法，根据采用不同的概率模型，还有很多细分。相比于遗传算法，EDA最大的特点就是种群产生的方式，通过概率分布来产生。因此，了解其中的概率模型的细节很重要。

Univariate marginal distribution algorithm (UMDA)

UMDA是一种简单的EDA，它通过估计所选择个体的边界概率，来建立模型。

从当前群体中选择 $\lambda$ 个个体组成繁殖群体 $S (t)$ 。

依据 $S (t)$ 建立模型如下：

$p_{t+1}(x_i)=\frac{1}{\lambda}\sum_{x\in S(t)}x_i,i=1,2,...,n$

Population-based incremental learning (PBIL)

PBIL算法是UMDA的一种改进，它通过增量的方式来建立概率模型。

同样，从当前群体中选择 $\lambda$ 个个体组成繁殖群体 $S (t)$ 。

依据 $S (t)$ 建立模型如下：

$p_{t+1}(x_i)=(1-\gamma)\cdot p_t(x_i)+\gamma\cdot \frac{1}{\lambda}\sum_{x\in S(t)}x_i$

其中， $\gamma \in (0,1]$ 是学习因子（learning rate）。

基于高斯模型的EDA：算法流程

随机生成初始种群 $P (0)$ ，初始化高斯模型的均值 $\mu$ 和方差 $\delta$ 。假设每维变量的高斯模型为： $\{N(\mu_1,\delta_1),...,N(\mu_n,\delta_n)\}$ ，n为自变量的维数；
抽样：根据各位自变量对应的高斯模型，抽样产生新种群 $T (t)$ ；
选择：从新种群种选择优秀个体集合 $S (t)$ ；
建模：计算 $S (t)$ 在各个变量上的均值与方差，对原有模型进行更新。
算法未达到结束条件，返回2，否则，退出。

均值更新模型如下：

$\mu_j^{t+1}=(1-\alpha)\cdot \mu_j^t+\alpha\cdot(x_{j}^{best,1}+x_{j}^{best,2}-x_{j}^{worst})$

方差更新模型如下：

$\delta_j^{t+1}=(1-\alpha)\cdot \delta_j^t+\alpha\cdot \sqrt{\frac{\sum_{k=1}^K(x_j^k-\bar{x}_j)}{K}}$

其中， $\alpha\in [0,1]$ 是学习因子，K为所选择的优秀个体数目， $\bar{x}$ 是所选择的优秀个体的平均值， $x^{best,1},x^{best,1}$ 是当前群体种最好的两个个体， $x^{worst}$ 是当前群体中的最差个体；

更新方式多种多样，也可以直接用优秀个体的均值和防擦好来替代原来的均值和方差。

Matlab 仿真实例

问题

求解下列函数的最大值：

$y=x_1\cdot cos(2\pi x_2)+x_2\cdot cos(2\pi x_1)$

分析

该问题可以采用PBIL算法进行实现，因为是求最大值，所以就选取目标函数作为适应度函数。

代码实现

代码参考博客²，我已经逐行注释，感兴趣的可以阅读一下代码细节，供参考学习使用。

% 问题 -2<x1, x2<2 y=x1 * cos(2*pi*x2) + x2 * cos(2*pi*x1)
%%%%%%%%%%%%PBIL algorithm
clc
clear
clf
tic         %开始计时
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%参数设置%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Pop_Size=40;                                            % 种群中个体数量
Variable_Num=2;                                         % 每个个体中种群的变量数
Individual_Len=20;                                      % 每个变量的长度(相当于一个二进制数)
Iteration_Times=1000;                                   % 进化次数
I=1;                                                    % 表示第几次进化过程
Learning_Rate=0.01;                                     % 学习速率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%产生初始种群%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Binary_X=zeros(Pop_Size,Variable_Num,Individual_Len);   % 生成值为0的种群矩阵Binary_X
for i=1:1:Pop_Size                                      % Pop_Size=40
    for j=1:1:Variable_Num                              % Variable_Num=2
        for k=1:1:Individual_Len                        % Individual_Len=20
            Binary_X(i,j,k)=round(rand());              % round函数用于四舍五入随机产生的值 rand()
        end                                             % 函数随机产生 0到1 之间的小数 round函数将小数四舍五入为0或1
    end
end
% zeros是MATLAB内的一个函数。
% 其功能是返回一个m×n×p×...的double类零矩阵。注意：m, n, p,...必须是非负整数
% 负整数将被当做0看待。
% 二维用法：zeros(m,n)或zeros(n)
% 功能：zeros(m,n)产生m×n的double类零矩阵，zeros(n)产生n×n的全0方阵。
Best_Individual=zeros(1,Iteration_Times);                               % 初始化值为0的优势种群矩阵，用于记录每次进化最好情况
Probability_Vector=zeros(Iteration_Times,Variable_Num,Individual_Len);  % 初始化概率向量矩阵
traces=zeros(3,Iteration_Times);                                        % 追踪每一代的最优值，trace为最优值矩阵，用来记录每一代的最优值
%%%%%%%%%%%%%%%%%%%%%%%%%%开始进行迭代%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while I<=Iteration_Times    
%%%%%%%%%%%%%%%%%%%%%%%将采样的值，由二进制转化到十进制%%%%%%%%%%%%%%%%%%%%%%
  Decimal_X=zeros(Pop_Size,Variable_Num);                               % 初始化十进制矩阵
    for i=1:1:Pop_Size
        for j=1:1:Variable_Num  
            k=Individual_Len;                                           % Individual_Len=20
            t=1;
            while k>=1%将二进制矩阵转化为十进制矩阵,便于后面进行排序
               Decimal_X(i,j)=Decimal_X(i,j)+Binary_X(i,j,k)*2^(t-1);   % 将一位二进制转化为十进制
               k=k-1;                                                   % 向左切换到下一位，进行进制转换
               t=t+1; 
            end
        end
    end
%%%%%%%%%%%%%%%%%%%%%%%%%%%将十进制映射到解空间中%%%%%%%%%%%%%%%%%%%%%%%%%%%
    Solution=zeros(Pop_Size,Variable_Num);                              % 初始化解空间矩阵（二维）
    for i=1:1:Pop_Size
        for j=1:1:Variable_Num
            Solution(i,j)= -2 + Decimal_X(i,j) * 4 / (2^Individual_Len-1);     % 存储每个个体对应变量的解
        end
    end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%计算适应值%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    Fitness_Value=zeros(1,Pop_Size);                                    % 初始化适应值矩阵（一维表针对每个个体）
    for i=1:1:Pop_Size                                                  % .*表示矩阵之间元素按位置相乘
        Fitness_Value(i)=Solution(i,1).*cos(2*pi*Solution(i,2))+Solution(i,2).*cos(2*pi*Solution(i,1));
    end                                                                 % 计算每个个体的适应值，相当于求f(x)的值，这里是求解函数的最大值
%%%%%%%%%%%%%%%%将适应值按照从小到大的顺序排序，并选出最优个体%%%%%%%%%%%%%%%
    [FitnessValue,index]=sort(Fitness_Value);                           % 排序适应值（升序），FinnessValue存储排序好的值，index存储对应值在原函数的索引
    Best_Individual(I)=Fitness_Value(index(Pop_Size));                  % 存储本次进化最优个体（升序）对应索引位置的值（最大的值）
    traces(1,I)=Solution(index(Pop_Size),1);                            % 存储每代最优个体各变量的值及最优值
    traces(2,I)=Solution(index(Pop_Size),2);
    traces(3,I)=Fitness_Value(index(Pop_Size));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%选出优势群体%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    Superiority_Polution=zeros(Pop_Size/2,Variable_Num,Individual_Len); % 只从所有个体选择一半作为优势个体，初始化优势种群矩阵
    for i=1:1:Pop_Size/2                                                % Pop_Size/2决定优势种群个体数
        for j=1:1:Variable_Num
            for k=1:1:Individual_Len
                Superiority_Polution(i,j,k)=Binary_X(index(i+Pop_Size/2),j,k);
            end                                                         % 由于之前是升序排序，且是选择一半优势个体所以优势个体都是从中间开始向后才有的
        end                                                             % 索引在这里起到了很重要的作用，不能使用FitnessValue矩阵因为矩阵内是十进制数
    end                                                                 % 而索引在这里可以帮助寻找原矩阵中的二进制数
%%%%%%%%%%%%%%%%从优势群体中统计基因位的值，来更新概率向量%%%%%%%%%%%%%%%%%%%
    Ones_Number=zeros(Variable_Num,Individual_Len);
    for i=1:1:Pop_Size/2
        for j=1:1:Variable_Num
            for k=1:1:Individual_Len
                if Superiority_Polution(i,j,k)==1                       % 如果优势种群中某个体中某变量中二进制串某一位为1
                    Ones_Number(j,k)=Ones_Number(j,k)+1;                % 让对应变量对应位在下次产生1的概率增加1
                end
            end
        end
    end
    for j=1:1:Variable_Num
        for k=1:1:Individual_Len
            Probability_Vector(I,j,k)=Ones_Number(j,k)/(Pop_Size/2);    % 更新每一变量每一位可能出现1概率向量采用百分比形式
        end                 
    end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%更新概率向量%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%       
if I>1                                                                  % 如果这不是第一次进化，进行增量学习
       for j=1:1:Variable_Num
           for k=1:1:Individual_Len
               % 这里结合了最优个体(此处只选择了一个，当然也可以选择多个)和上一代的概率得到这一带的概率
               Probability_Vector(I,j,k)=Learning_Rate.*Binary_X(index(Pop_Size),j,k)+(1-Learning_Rate).*Probability_Vector(I-1,j,k);
           end
       end
end
%%%%%%%%%%%%%%%%%%%%%%%%根据概率向量对解空间采样%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:1:Pop_Size                          % 这里针对上面得到的最新概率，重新产生新的种群
        for j=1:1:Variable_Num
            for k=1:1:Individual_Len
                r=rand();                       % 随机生成数0到1之间的小数r
                if r<Probability_Vector(I,j,k)  % 如果r小于概率向量的值，对应为1
                    Binary_X(i,j,k)=1;          % 种群矩阵为1
                else    
                    Binary_X(i,j,k)=0;          % 否种群矩阵为0
                end
            end
        end
    end                 % 执行如上操作就得到了下一代群体
   I=I+1;               % 进化次数+1
end                     % 迭代终止
toc                     % 计时终止，显示程序运行所用
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%生成种群演化图%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
figure(1)                       % 生成画图窗口
hold on
%hold on是当前轴及图像保持而不被刷新，准备接受此后将绘制的图形，多图共存
%hold off使当前轴及图像不再具备被刷新的性质，新图出现时，取消原图。即关闭图形保持功能。
xlabel('进化代数')              % X轴名称为进化代数
ylabel('最优解的变化')          % Y轴名称为最优解的变化
title('进化过程')               % 图像名为进化过程
plot(Best_Individual);          % 根据每代种群中最优个体绘制函数图像
grid on                         % grid on为显示函数网格线  grid off 为隐藏函数网格线
[Best_Polution,xuhao_Iteration]=max(Best_Individual);   % 获取最优个体
bestx1=traces(1,xuhao_Iteration);                       % 获取最优个体参数1
bestx2=traces(2,xuhao_Iteration);                       % 获取最优个体参数2
bestz=traces(3,xuhao_Iteration);                        % 获取最优个体值
% 打印结果
fprintf(['最优解:\nx1=',num2str(bestx1),'\nx2=',num2str(bestx2),'\nf=',num2str(bestz),'\niteration=',num2str(xuhao_Iteration),'\n']);
hold off
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%