这里写目录标题
- learning rate
- 单一固定(one-size-fits-all)的学习率Model训练到驻点很困难(学习率太大不能收敛,学习率太小收敛太慢)
- 如何客制化学习率?- 引入参数σ
- σ常见的计算方式 - Root mean square(均方根)
- Adagrad - 不同参数不同学习率
- RMSProp - 不同参数不同学习率+同一参数不同学习率
- Adam:RMSProp + Momentum
- 小梯度累加导致learning rate 暴增
- 如何让时间影响学习率? - 方式一:Learning Rate Decay(学习速率衰减)
- 如何让时间影响学习率? - 方式二:Warm Up(预热)
learning rate
loss下降到走不下去的时候,gradient真的很小吗?不一定噢,不一定卡在local minimal还是saddle point
思考训练卡住的原因是,
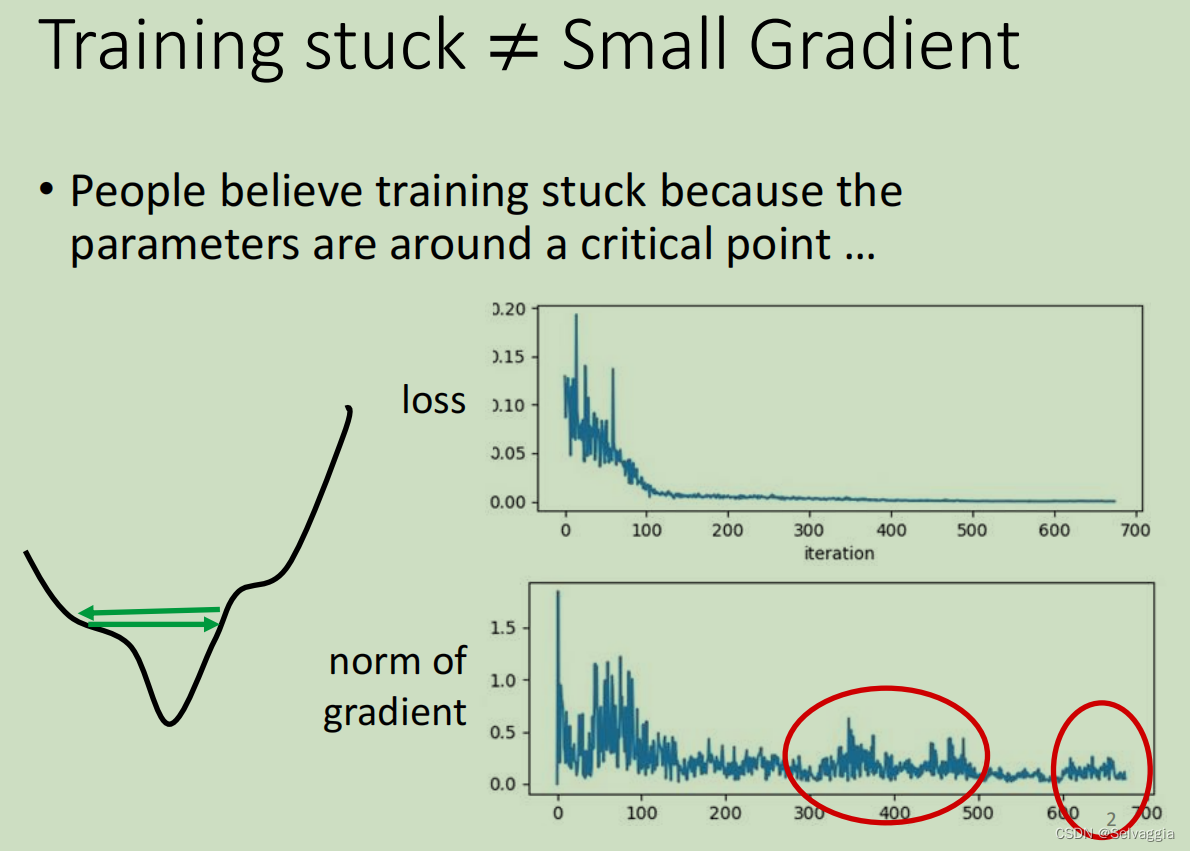
通过观察norm(向量) of gradient
loss几乎没动了,gradient还是有上升下降的波动的痕迹
梯度下降可能会发生锯齿现象
用一般的gradient decent往往做不到如图(由于遇到minimal point或者是saddle point,loss无法继续下降)的效果,往往在gradient decent还很大的时候,loss就下不去了
多数training在还没走到critical point的时候就已经停止了
当loss不再下降时,并不一定是gradient很小的情况(saddle point 或者 local minima),也有可能是gradient在error surface山谷的两个谷壁间不断的来回的震荡导致loss不能再下降。
单一固定(one-size-fits-all)的学习率Model训练到驻点很困难(学习率太大不能收敛,学习率太小收敛太慢)
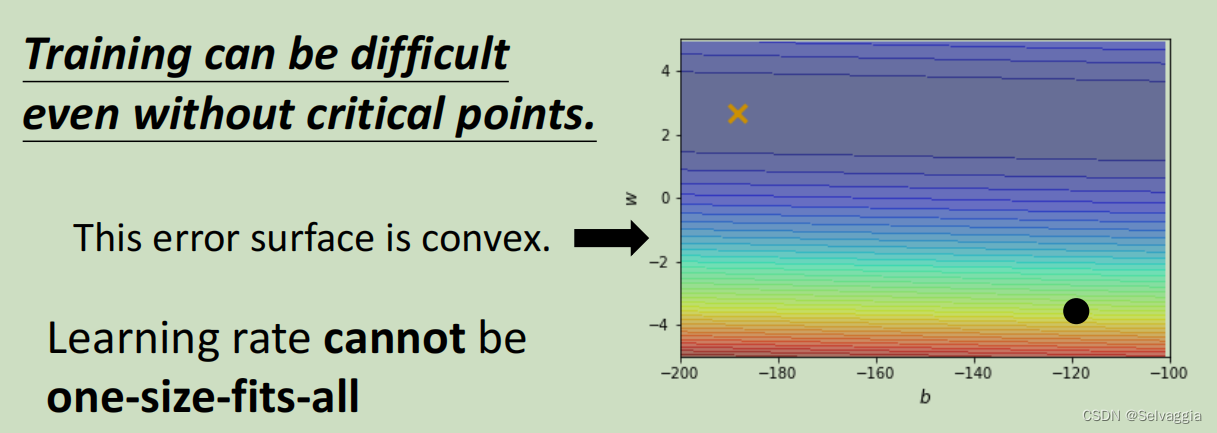
以上图为例子,只有两个参数,这两个参数值不一样的时候Loss的值不一样,画出了error surface,这个error surface的最低点在上图黄色X的地方。事实上,这个error surface是convex的形状(可以理解为凸的或者凹的,convex optimization常翻译为“凸优化”)。
这个非常简单的error surface ,在纵向的变化特别密集((gradient非常的大,它的坡度的变化非常的大、非常的陡峭)),在横向的变化特别平滑(gradient非常的小,它的坡度的变化非常的小、非常的平滑),可以理解成上面的“等高线”是一个长轴特别长,短轴特别短的椭圆。我们现在要从黑点这个地方当作初始点,目标的最佳点是×所在的位置。
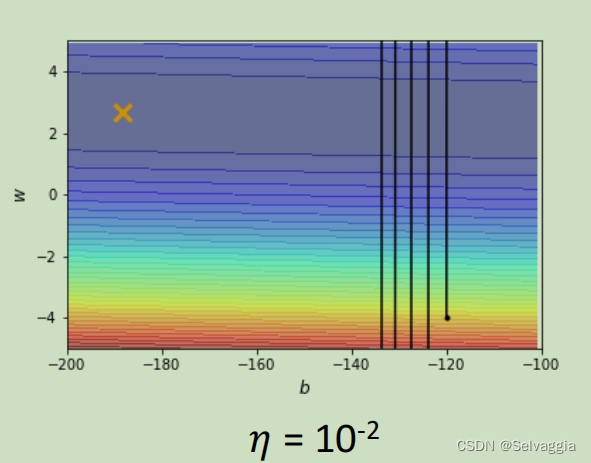
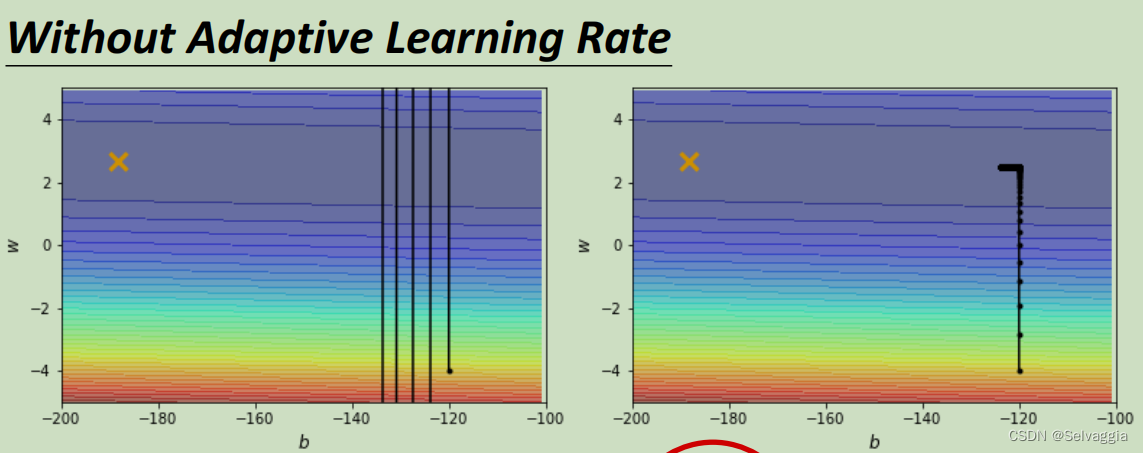
当learning rate设为 1 0 − 2 10^{-2} 10−2 的时候,这个参数在峡谷的两端不断的震荡从而导致loss掉不下去,但此时的gradient仍然很大。
那你可能说是因为learning rate设太大了,learning rate决定了我们update参数的时候步伐有多大,learning rate步伐太大,没办法慢慢地滑到山谷里面,只要把learning rate设小一点不就可以解决这个问题了吗? 调这个learning rate从10⁻²一直调到10⁻⁷终于不再震荡。
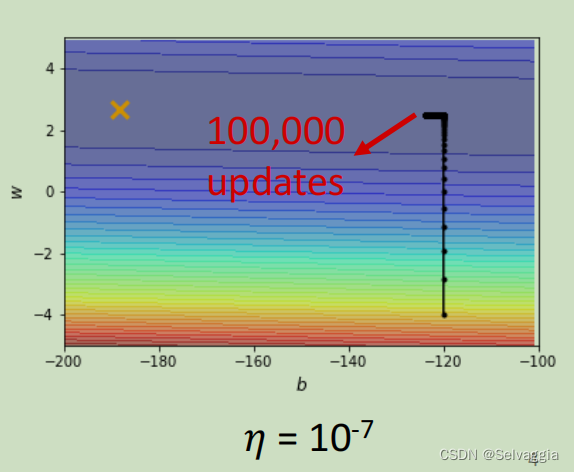
但是这个训练此时永远走不到终点,因为learning rate已经太小了,上图中垂直竖线,因为坡度很陡、gradient的值很大,所以还能够前进一点;左拐以后在横短黑线这个地方坡度已经非常平滑了,非常小的gradient 和 这么小的learning rate根本没有办法再让训练前进 ( θ i + 1 = θ i − η g ) ( \theta _{i + 1} = θ_ i − η g ) (θi+1=θi−ηg)
事实上在左拐这个地方,这一大堆黑点有十万个,所以显然就算是一个convex的error surface,你用gradient descend也很难train。
在之前的gradient descend中,所有的参数都是设同样的learning rate,这显然不太合适,learning rate它应该要根据不同的参数进行定制,也就是客制化。
如何客制化学习率?- 引入参数σ
Different parameters needs different learning rate(不同的参数需要不同的学习率)
那客制化学习率的方法是什么? 从刚才的例子中,其实可以看到一个大原则,如果在某一个方向上的gradient的值很小,非常的平坦,那我们会希望learning rate调大一点;如果在某一个方向上非常的陡峭,坡度很大,那我们其实期待learning rate可以设得小一点。 也就是说希望学习率可以根据梯度的情况进行调整
接下来看σ常见的计算方式。
σ常见的计算方式 - Root mean square(均方根)
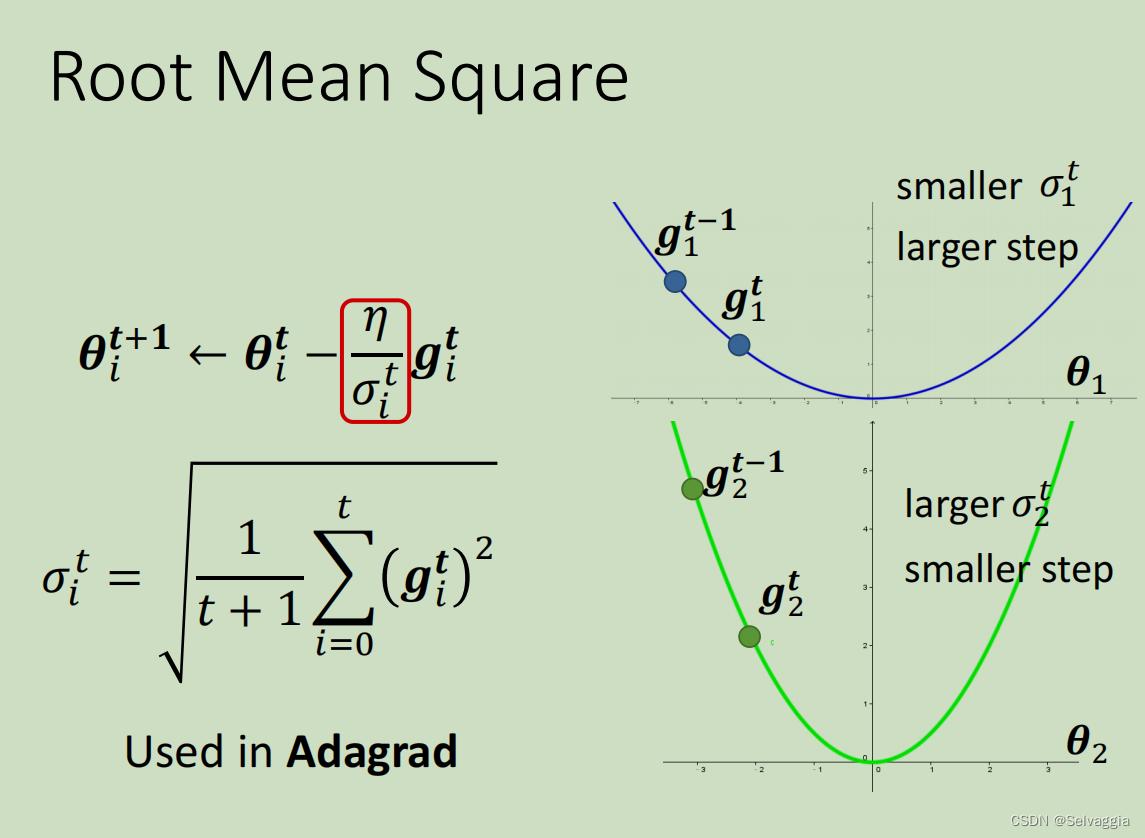
Adagrad - 不同参数不同学习率
上面这个方法被应用在Adagrad算法中,Adagrad解决不同参数应该使用不同的更新速率的问题。Adagrad是自适应地为各个参数分配不同学习率的算法。
以上版本绝非最终版本
Root Mean Square中,每一个gradient都有同等的重要性,
但在RMS Prop中,你可以自己调整gradient的重要性或权重。
通过参数设置来决定,是当前的gradient更具有决定性还是之前的gradient更具有决定性
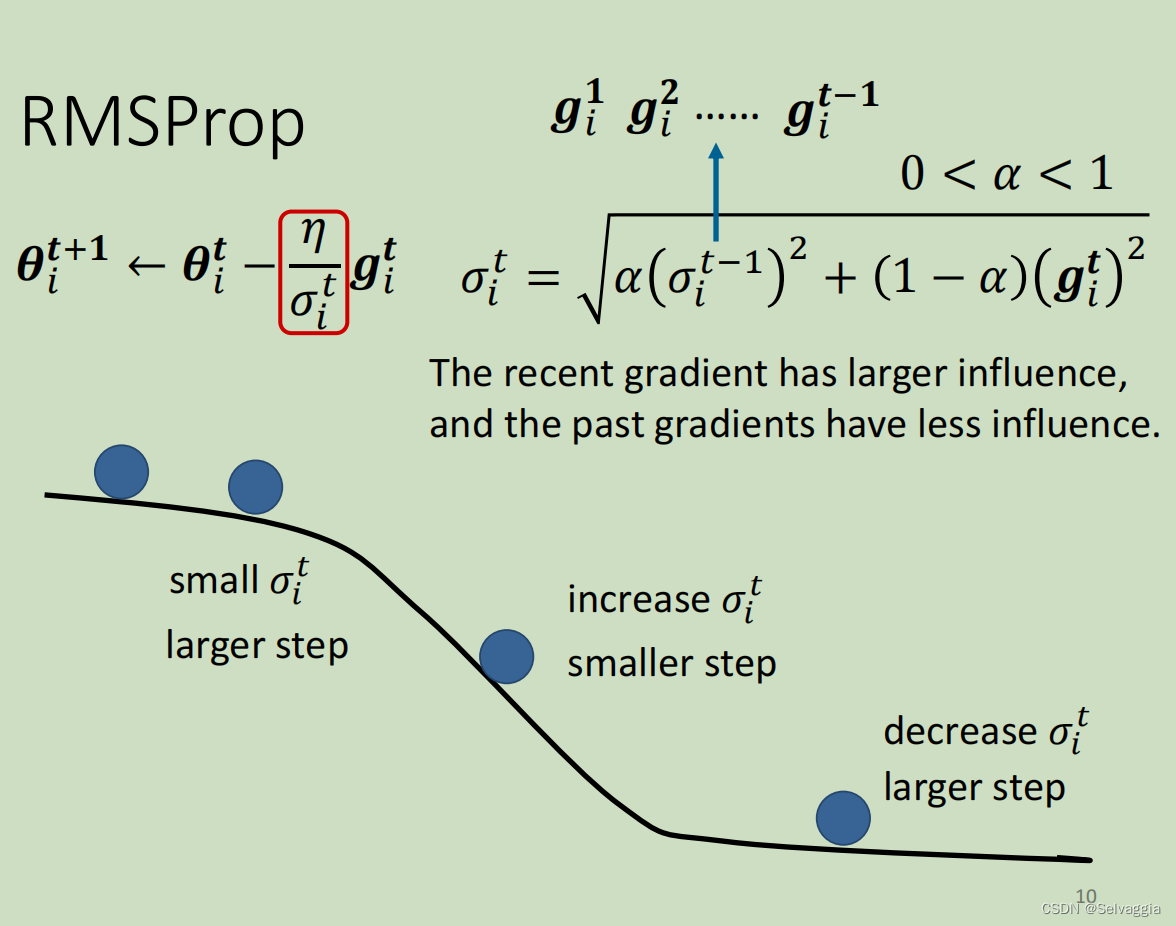
RMSProp - 不同参数不同学习率+同一参数不同学习率
root mean square prop:均方根传递
我们期望:就算是同一个参数,它需要的learning rate也会随著时间而改变。
上面的方法中我们假设,同一个参数,其gradient的大小差不多。
但事实上并不是这样,比如下图这个例子,心月形的error surface
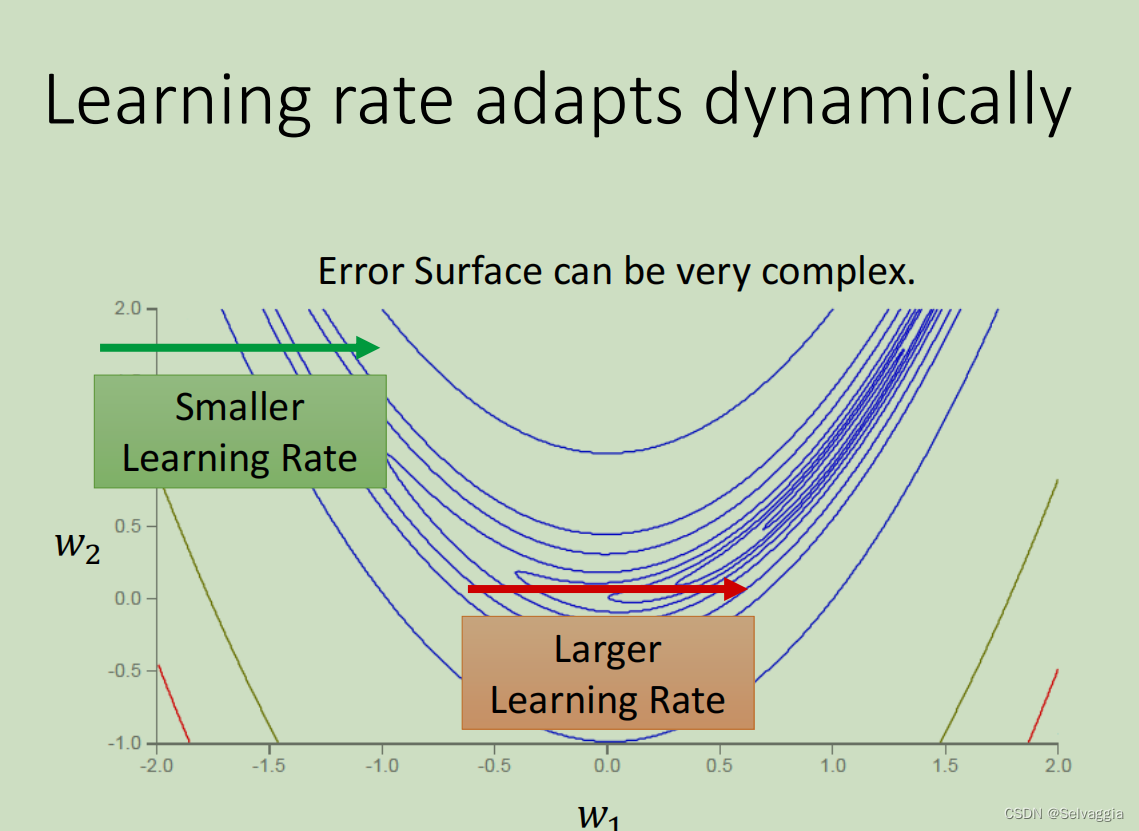
【 红色箭头处相比于绿色箭头处的gradient是比较平缓的,下面那个穿过很多相同的等高线,等于穿过一个平滑的小谷地
maybe need some knowledge about 自然地理??】
红色和绿色线的方向,可以看做同一个参数w2的同一个方向,所以就算是同一个参数的同一个方向,也需要learning rate可以动态的调整。于是就有了RMS Prop。
RMS Prop 不是出自论文,只是Hinton在自己的deep learning课程中提出的。
Adam:RMSProp + Momentum
Adam是现在最常用的optimization的策略。
Adam就是RMS Prop加上Momentum,Adam的演算法跟原始的论文
在pytorch中都帮你把算法写好了,所以不用担心这种optimization的问题。optimizer的deep learning套件往往都做好,然后这个optimizer里面也有一些hyperparameter需要人工决定,但是你往往用预设的那一种参数就可以了,自己调有时候会调到比较差的。
小梯度累加导致learning rate 暴增
小梯度累加导致learning rate 暴增
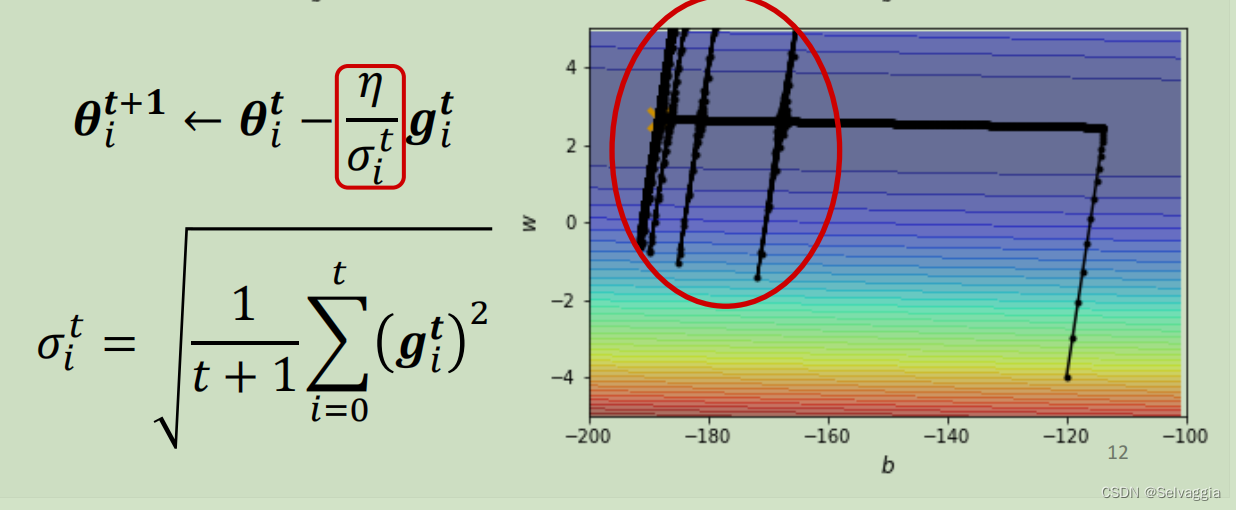
如何处理梯度爆炸?- 让时间影响学习率
如何处理这种“爆发”问题,有一个方法叫做learning rate scheduling可以解决。
如何让时间影响学习率? - 方式一:Learning Rate Decay(学习速率衰减)
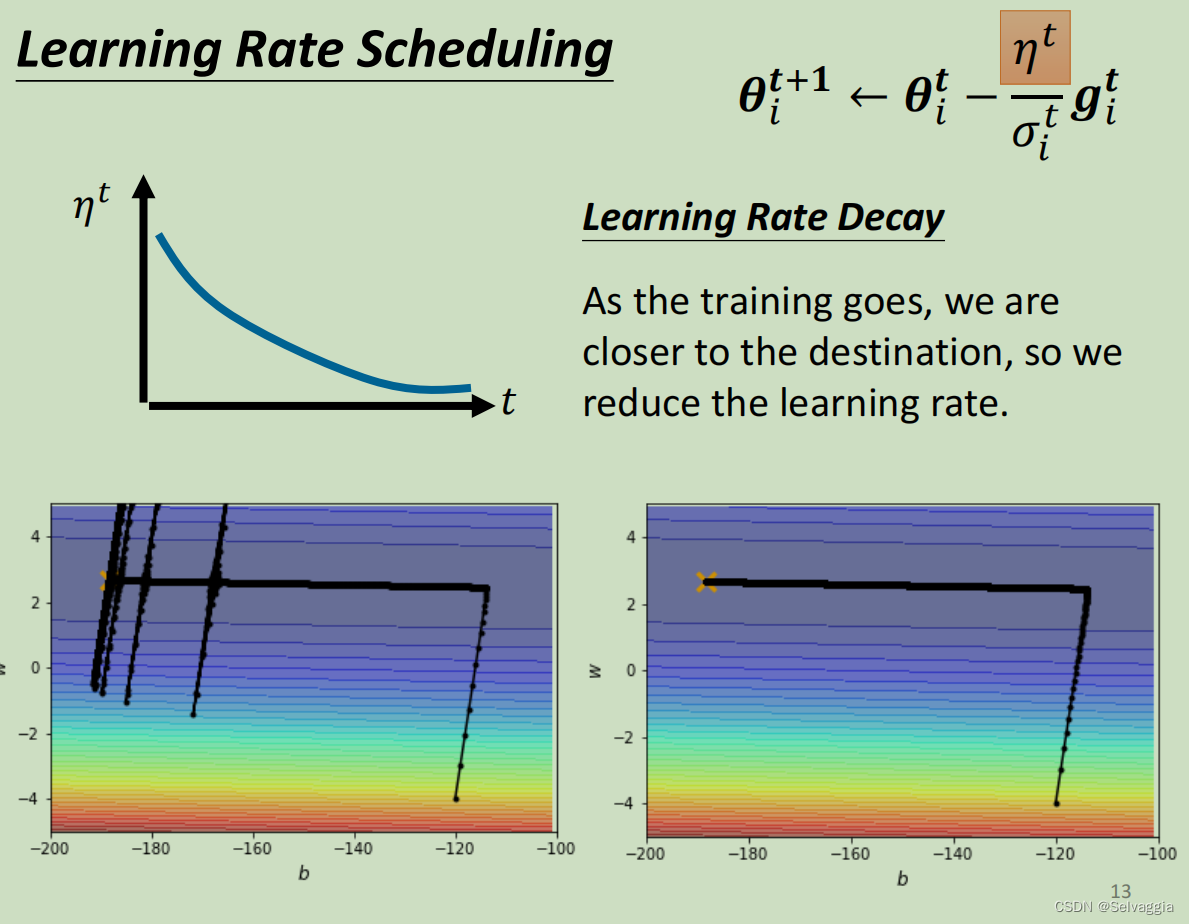
最常见的方法叫做Learning Rate Decay(学习速率衰减),也就是说随着时间的不断地前进、随着参数不断的update,让η越来越小。
如何让时间影响学习率? - 方式二:Warm Up(预热)
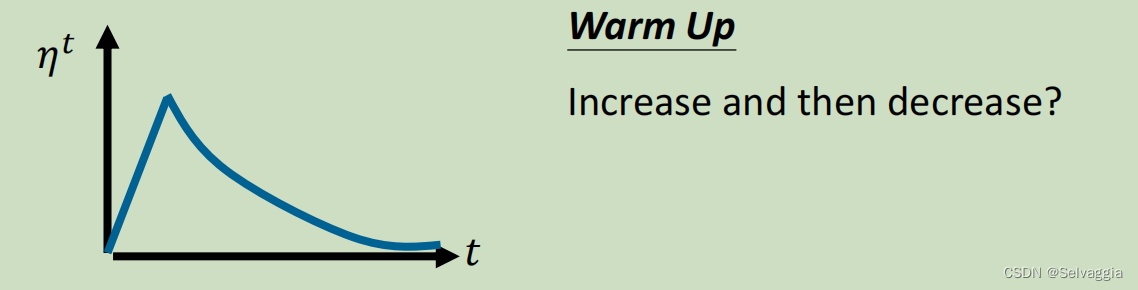
为什么warm up会起作用?- 待研究
一个可能的解释:σ是一个统计量,刚开始时,因为σ没有收集到足够的数据,先让η很小,学习率很小,步子很小,让σ有足够的时间收集更多的error surface的情况,等到σ收集到足够的情况可以做出很好的统计。
博主造福后辈!!!