UVa1354，ACM/ICPC Tokyo 2005，Mobile Computing（天平难题）

news2024/11/18 14:28:12

1、题目

在这里插入图片描述

2、题意

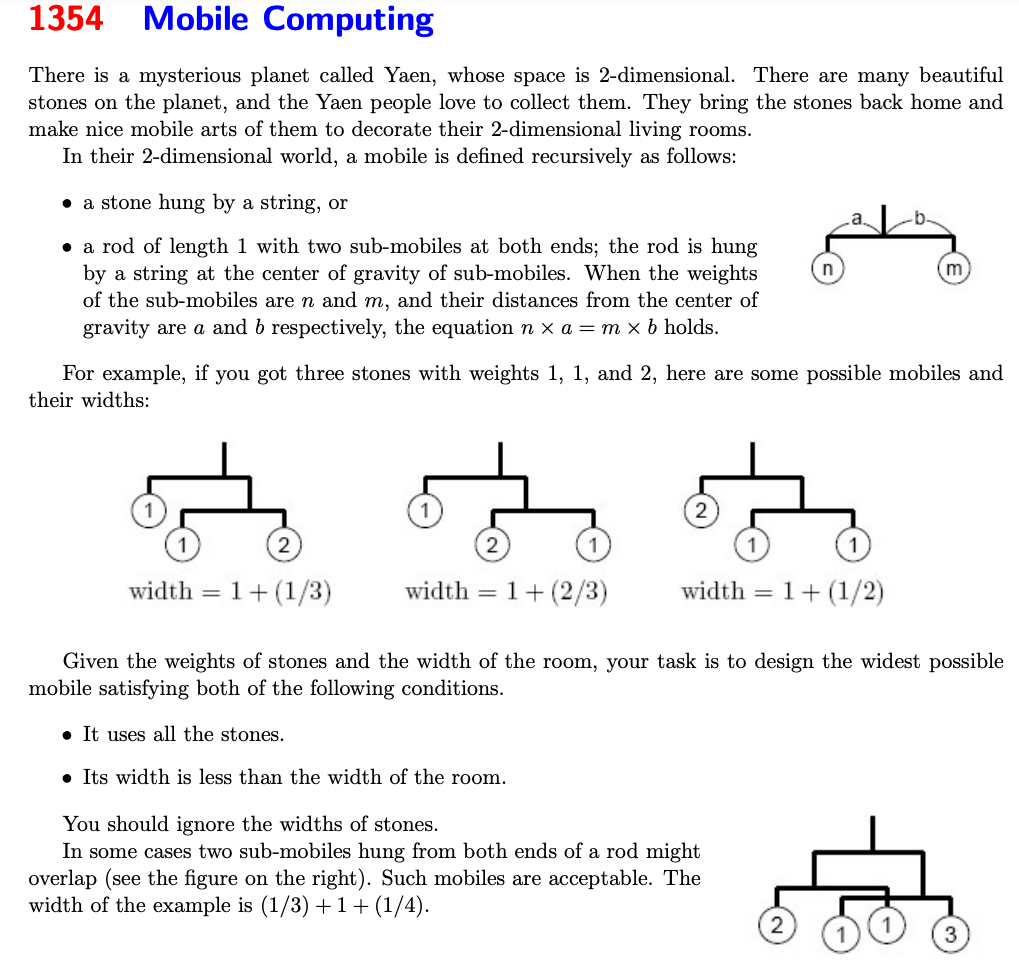
给出房间的宽度 $r$ 和 $s$ 个挂坠的重量 $w_i$ 。设计一个尽量宽（但宽度不能超过房间宽度 $r$ ）的天平，挂着所有挂坠。

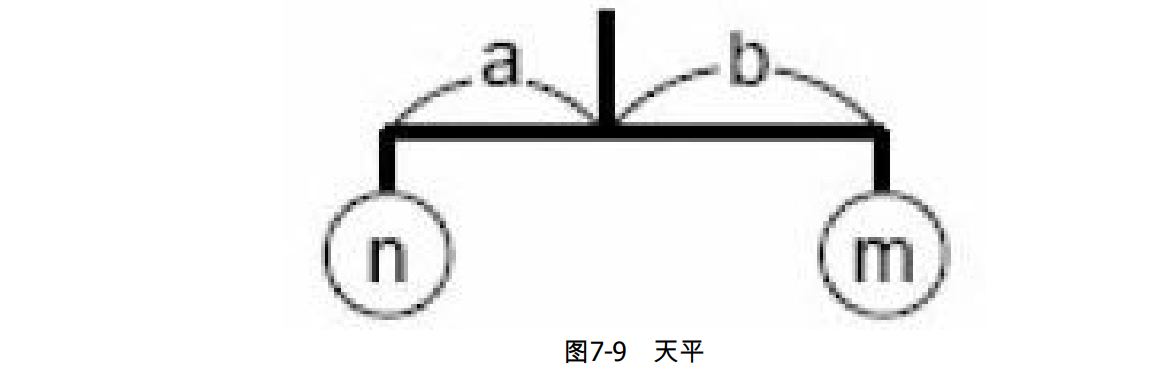
天平由一些长度为1的木棍组成。木棍的每一端要么挂一个挂坠，要么挂另外一个木棍。如图7-9所示，设 $n$ 和 $m$ 分别是两端挂的总重量，要让天平平衡，必须满足 $n * a = m * b$ 。
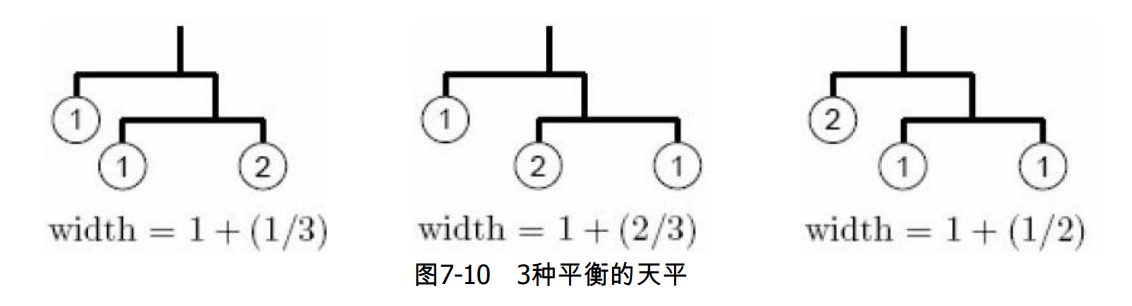
在这里插入图片描述
例如，如果有3个重量分别为1, 1, 2的挂坠，有3种平衡的天平，如图7-10所示。

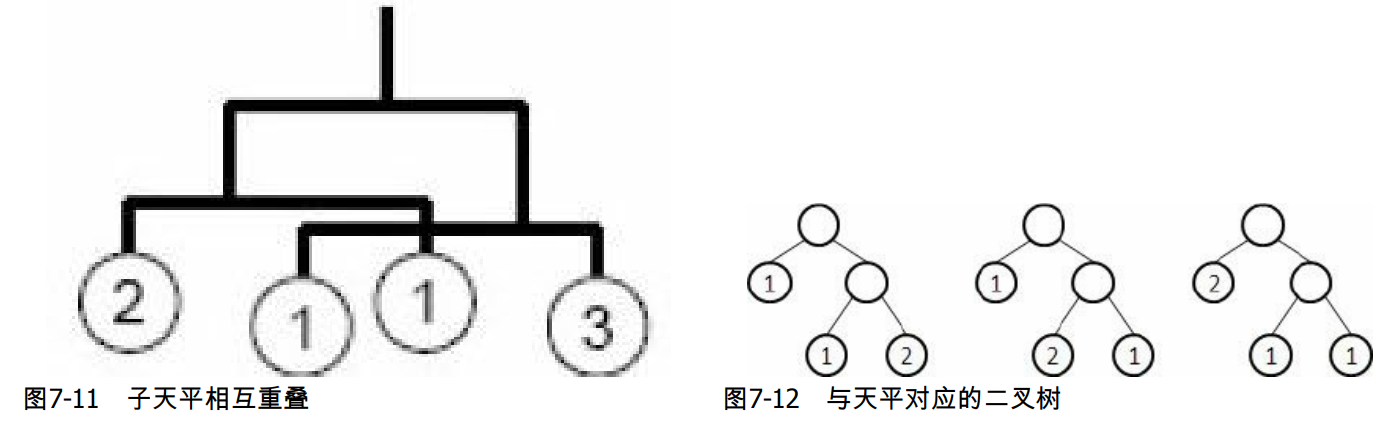
挂坠的宽度忽略不计，且不同的子天平可以相互重叠。如图7-11所示，宽度为 $(1/3) + 1 + (1/4)$ 。

输入第一行为数据组数。每组数据前两行为房间宽度 $r$ 和挂坠数目 $s$ （ $0 < r < 10$ ， $1 \leq s \leq 6$ ）。以下 $s$ 行每行为一个挂坠的重量 $w_i（1≤w_i≤1000）$ 。输入保证不存在天平的宽度恰好在 $r-10 ^{-5}$ 和 $r+10^{-5}$ 之间（这样可以保证不会出现精度问题）。

对于每组数据，输出最优天平的宽度。如果无解，输出-1。你的输出和标准答案的绝对误差不应超过10^-8。

3、分析

如果把挂坠和木棍都作为结点，则一个天平对应一棵二叉树，如题目中给出的，挂坠为1, 1, 2的3个天平如图7-12所示。
在这里插入图片描述

对于一棵确定二叉树，可以计算出每个挂坠的确切位置，进而计算出整个天平的宽度，所以本题的核心任务是：枚举二叉树。

如何枚举二叉树呢？最直观的方法是沿用回溯法框架，每次选择两个结点组成一棵子树，递归 $s - 1$ 层即可。以4个挂坠1, 1, 2, 3为例，下面是解答树的一部分（每个结点的子树并没有全部画出），如图7-13所示。
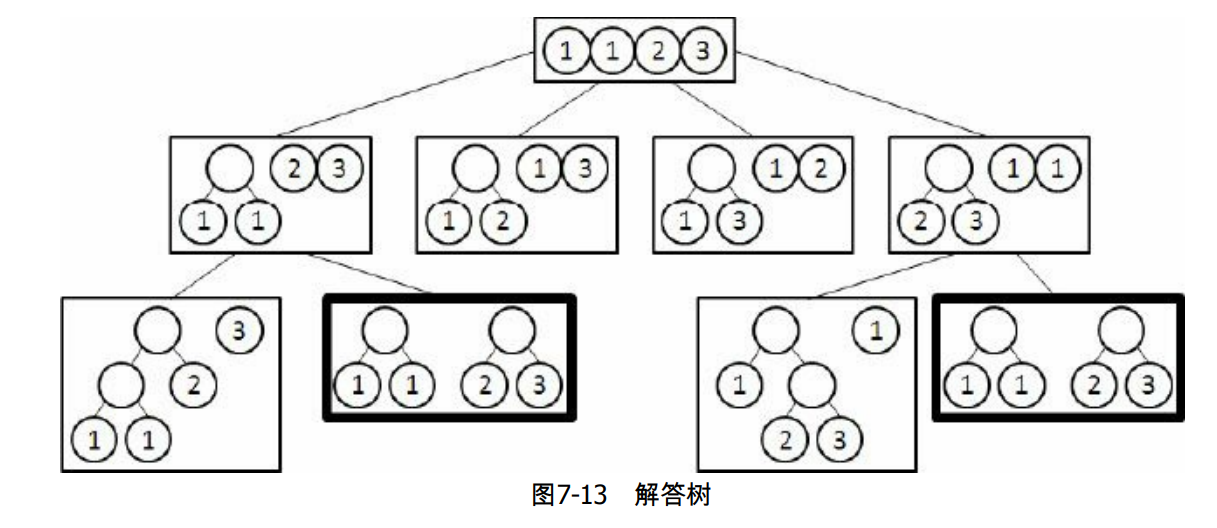
在这里插入图片描述
上面的方法已经足够解决本题，但还有优化的余地，因为有些二叉树被枚举了多次（如图7-13中的两个粗框结点）。

推荐的枚举方法是：自顶向下构造，每次枚举左子树用到哪个子集，则右子树就是使用剩下的子集。

4、代码实现

// UVa1354 Mobile Computing
// Rujia Liu
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;

struct Tree {
  double L, R; // distance from the root to the leftmost/rightmost point
  Tree():L(0),R(0) {}
};

const int maxn = 6;

int n, vis[1<<maxn];
double r, w[maxn], sum[1<<maxn];
vector<Tree> tree[1<<maxn];

void dfs(int subset) {
  if(vis[subset]) return;
  vis[subset] = true;

  bool have_children = false;
  for(int left = (subset-1)&subset; left; left = (left-1)&subset) {
    have_children = true;

    int right = subset^left;
    double d1 = sum[right] / sum[subset];
    double d2 = sum[left] / sum[subset];

    dfs(left); dfs(right);

    for(int i = 0; i < tree[left].size(); i++)
      for(int j = 0; j < tree[right].size(); j++) {
        Tree t;
        t.L = max(tree[left][i].L + d1, tree[right][j].L - d2);
        t.R = max(tree[right][j].R + d2, tree[left][i].R - d1);
        if(t.L + t.R < r) tree[subset].push_back(t);
      }
  }

  if(!have_children) tree[subset].push_back(Tree());
}

int main() {
  int T;
  scanf("%d", &T);
  while(T--) {
    scanf("%lf%d", &r, &n);
    for(int i = 0; i < n; i++) scanf("%lf", &w[i]);
    for(int i = 0; i < (1<<n); i++) {
      sum[i] = 0;
      tree[i].clear();
      for(int j = 0; j < n; j++)
        if(i & (1<<j)) sum[i] += w[j];
    }

    int root = (1<<n)-1;
    memset(vis, 0, sizeof(vis));
    dfs(root);

    double ans = -1;
    for(int i = 0; i < tree[root].size(); i++)
      ans = max(ans, tree[root][i].L + tree[root][i].R);
    printf("%.10lf\n", ans);
  }
  return 0;
}