LeetCode 1465. 切割后面积最大的蛋糕

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：
horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离
verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出面积最大的那份蛋糕，并返回其面积。由于答案可能是一个很大的数字，因此需要将结果对 109 + 7 取余后返回。

示例 1：
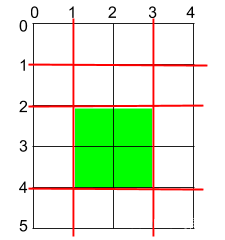
在这里插入图片描述

输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

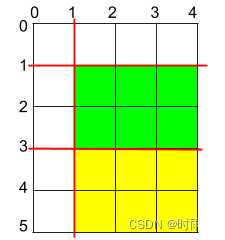
在这里插入图片描述

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。
示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

2 <= h, w <= 109
1 <= horizontalCuts.length <= min(h - 1, 105)
1 <= verticalCuts.length <= min(w - 1, 105)
1 <= horizontalCuts[i] < h
1 <= verticalCuts[i] < w

题目数据保证 horizontalCuts 中的所有元素各不相同
题目数据保证 verticalCuts 中的所有元素各不相同

题目给出一个高度为 hhh 长度为 www 的矩形蛋糕，我们需要按照水平切割方案
horizontalCuts\textit{horizontalCuts}horizontalCuts，和竖直切割方案 verticalCuts\textit{verticalCuts}verticalCuts 对蛋糕进行切割，其中 horizontalCuts[i]\textit{horizontalCuts}[i]horizontalCuts[i] 表示从矩形蛋糕顶部水平往下距离 horizontalCuts[i]\textit{horizontalCuts}[i]horizontalCuts[i] 的位置进行切割，verticalCuts[j]\textit{verticalCuts}[j]verticalCuts[j] 表示从矩形蛋糕最左侧往右距离 verticalCuts[j]\textit{verticalCuts}[j]verticalCuts[j] 的位置进行切割。现在我们需要求出切割后的面积最大的蛋糕面积对 109+710 ^ 9 + 710 9 +7 取模后的值。

首先，我们需要将水平切割和竖直切割的位置数组 horizontalCuts\textit{horizontalCuts}horizontalCuts 和 verticalCuts\textit{verticalCuts}verticalCuts 进行排序，并且在数组的开头添加 000 和结尾添加对应的矩形边界值。这是为了确保我们考虑到所有的切割位置，包括矩形的边缘。然后在排序后的切割位置数组中，我们可以计算相邻切割位置之间的间隔，以找出水平和竖直切割的最大间隔。因为每个间隔代表了一块蛋糕的尺寸，水平和竖直间隔的乘积就是对应蛋糕块的面积，所以最大面积由最大水平间隔和最大竖直间隔相乘得到。最后我们返回最大面积对 109+710^9 + 710
9+7 的取模即可。

在这里插入图片描述

C++

class Solution {
public:
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        horizontalCuts.push_back(0);
        horizontalCuts.push_back(h);
        verticalCuts.push_back(0);
        verticalCuts.push_back(w);
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        int x = 0, y = 0;
        for (int i = 1; i < horizontalCuts.size(); ++i) {
            x = max(x, horizontalCuts[i] - horizontalCuts[i - 1]);
        }
        for (int i = 1; i < verticalCuts.size(); ++i) {
            y = max(y, verticalCuts[i] - verticalCuts[i - 1]);
        }
        const int mod = 1e9 + 7;
        return (1ll * x * y) % mod;
    }
};

这个代码实现了一个计算蛋糕切割后最大面积的算法。它的思路是，首先将水平切割和竖直切割的位置信息添加到对应的数组中，然后对数组进行排序。接着，通过遍历这些切割位置，计算相邻两个位置之间的距离，从而得到切割后的矩形条的最大宽度和最大高度。最后，计算最大面积并返回。

这个算法的时间复杂度是O(nlogn)，其中n是切割位置的数量。在排序时，使用了额外的O(n)的空间来存储排序后的数组。因此，这个算法的空间复杂度也是O(n)。

这个算法的优点是，它通过排序和遍历操作，直接得到了切割后矩形的最大宽度和最大高度，从而避免了复杂的动态规划计算。同时，它也使用了取模运算来防止结果溢出，从而保证了答案的正确性。

需要注意的是，这个算法假设切割位置的信息已经按照顺序给出了，并且没有考虑切割位置之间的间隔。如果存在间隔，需要对输入进行一些预处理，比如在每个切割位置之间插入0或其他默认值。此外，对于非数值型的切割位置，需要将其转换为数值型才能使用这个算法。

时间复杂度 O(mlog⁡m+nlog⁡n)O(m\log m + n\log n)O(mlogm+nlogn)，空间复杂度 O(max⁡(log⁡m,log⁡n))O(\max(\log m, \log n))O(max(logm,logn))

其中 mmm 和 nnn 分别为 horizontalCuts 和 verticalCuts 的长度。

python

class Solution:
    def maxArea(
        self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]
    ) -> int:
        horizontalCuts.extend([0, h])
        verticalCuts.extend([0, w])
        horizontalCuts.sort()
        verticalCuts.sort()
        x = max(b - a for a, b in pairwise(horizontalCuts))
        y = max(b - a for a, b in pairwise(verticalCuts))
        return (x * y) % (10**9 + 7)

首先，函数将矩形的起始和结束位置（0,0）和(h,w)添加到各自的切割列表中。这样做是为了确保这些位置也被视为可能的切割点。

然后，这两个列表分别进行排序。这是为了确保在查找可能的切割点时，它们是按照从左到右的顺序排列的。

接下来，函数使用pairwise函数从horizontalCuts和verticalCuts列表中分别生成一系列连续的切割点对，并计算相邻点之间的最大差值。这样做是为了找出可能的切割宽度和高度。

最后，函数返回这个最大面积值（使用取模操作，以防结果超过10^9+7）。

java

class Solution {
    public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
        final int mod = (int) 1e9 + 7;
        Arrays.sort(horizontalCuts);
        Arrays.sort(verticalCuts);
        int m = horizontalCuts.length;
        int n = verticalCuts.length;
        long x = Math.max(horizontalCuts[0], h - horizontalCuts[m - 1]);
        long y = Math.max(verticalCuts[0], w - verticalCuts[n - 1]);
        for (int i = 1; i < m; ++i) {
            x = Math.max(x, horizontalCuts[i] - horizontalCuts[i - 1]);
        }
        for (int i = 1; i < n; ++i) {
            y = Math.max(y, verticalCuts[i] - verticalCuts[i - 1]);
        }
        return (int) ((x * y) % mod);
    }
}

代码中使用了动态规划的思想，将原问题分解为子问题来求解。首先，对水平和垂直切割线进行排序，然后分别计算每一行和每一列的最长距离。接着，将矩形的宽度和高度减去最长的距离，得到剩余的宽度和高度。最后，取剩余宽度和高度中的最大值，即为路径的长度。

在代码实现中，使用了一个辅助函数dp来计算子问题的最优解。首先初始化两个dp数组，分别表示每一行和每一列的最长距离。然后遍历每一行和每一列，计算当前行或列的最长距离，并更新dp数组。最后返回路径的长度。

这个算法的时间复杂度为O(m*n)，其中m和n分别为水平切割线和垂直切割线的数量。由于该算法只需要遍历一次切割线，因此时间复杂度可以进一步优化为O(min(m,n))。

GO

func maxArea(h int, w int, horizontalCuts []int, verticalCuts []int) int {
	horizontalCuts = append(horizontalCuts, []int{0, h}...)
	verticalCuts = append(verticalCuts, []int{0, w}...)
	sort.Ints(horizontalCuts)
	sort.Ints(verticalCuts)
	x, y := 0, 0
	const mod int = 1e9 + 7
	for i := 1; i < len(horizontalCuts); i++ {
		x = max(x, horizontalCuts[i]-horizontalCuts[i-1])
	}
	for i := 1; i < len(verticalCuts); i++ {
		y = max(y, verticalCuts[i]-verticalCuts[i-1])
	}
	return (x * y) % mod
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

RUST

impl Solution {
    pub fn max_area(h: i32, w: i32, mut horizontal_cuts: Vec<i32>, mut vertical_cuts: Vec<i32>) -> i32 {
        const MOD: i64 = 1_000_000_007;

        horizontal_cuts.sort();
        vertical_cuts.sort();

        let m = horizontal_cuts.len();
        let n = vertical_cuts.len();

        let mut x = i64::max(horizontal_cuts[0] as i64, h as i64 - horizontal_cuts[m - 1] as i64);
        let mut y = i64::max(vertical_cuts[0] as i64, w as i64 - vertical_cuts[n - 1] as i64);

        for i in 1..m {
            x = i64::max(x, horizontal_cuts[i] as i64 - horizontal_cuts[i - 1] as i64);
        }

        for i in 1..n {
            y = i64::max(y, vertical_cuts[i] as i64 - vertical_cuts[i - 1] as i64);
        }

        ((x * y) % MOD) as i32
    }
}