题目列表

2908. 元素和最小的山形三元组 I

2909. 元素和最小的山形三元组 II

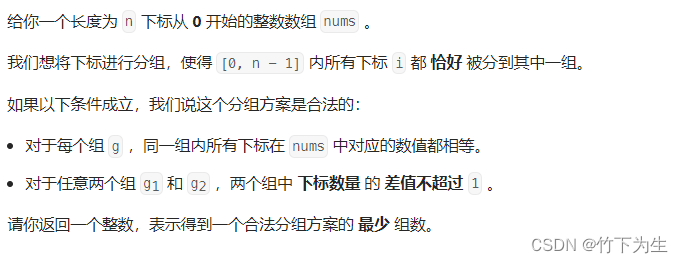
2910. 合法分组的最少组数 

2911. 得到 K 个半回文串的最少修改次数

一、元素和最小的山形三元组I

 

没什么好说的，不会其他方法就直接暴力，时间复杂度O(n^3)，代码如下

class Solution {
public:
    int minimumSum(vector<int>& nums) {
        int n=nums.size();
        int ans=INT_MAX;
        for(int i=0;i<n;i++)
            for(int j=i+1;j<n;j++)
                for(int k=j+1;k<n;k++)
                    if(nums[i]<nums[j]&&nums[j]>nums[k])
                        ans=min(ans,nums[i]+nums[j]+nums[k]);
        return ans==INT_MAX?-1:ans;
    }
};

 二、元素和最小的山形三元组II

这题和上一题一样，只是数据范围变大，需要优化时间复杂度，这也是老套路了，直接先预处理出前后缀最小值就行，然后枚举中间的那个元素，O(n)时间复杂度，代码如下

class Solution {
public:
    int minimumSum(vector<int>& nums) {
        int n=nums.size(),ans=INT_MAX;
        int suf[n];
        suf[n-1]=nums.back();
        for(int i=n-2;i>=0;i--)
            suf[i]=min(suf[i+1],nums[i]);
        for(int i=1,pre=nums[0];i<n-1;i++){
            if(pre<nums[i]&&nums[i]>suf[i+1])
                ans=min(ans,pre+nums[i]+suf[i+1]);
            pre=min(pre,nums[i]);
        }
        return ans==INT_MAX?-1:ans;
    }
};

三、合法分组的最少组数

这题还是有点难度的，但是思路还是很明显，先统计数字出现的次数，然后对相同数字进行分组，使得分出的组满足两个条件。关键是如何满足这两个条件，第一个已经满足了，主要看第二个

而第二个条件，其实已经在提醒我们需要枚举分组数量了，因为它限制了每个组的数量只能是x/x+1，都限定这么死了，你不枚举真的是可惜了，当然有人会想到二分，其实这题如果是枚举每个组的数量的话，是不满足二段性的(如果有能二分的方法，欢迎大家在评论区留言)

那么我来举个例子讲讲为什么不能二分？即为什么不满足二段性？其实我们在想二段性的时候，应该能感觉的出来这个二段性不是很"明确"，因为它能被分成每组两个元素，和它能被分成每组三个元素没有必然关系，下面举个例子

假设我们要将7个1分成最少组，很显然如果每组的个数是7/8，肯定可以，如果每组的个数是6/7也是可以的，如果每组的个数是5/6，就不可以了，但是如果每组的个数是3/4，那么又可以了，所以不具有二段性，所以我们选择从大往小枚举，遇到的第一个符合条件的个数就是最优解

有人可能会对上面的枚举方法感到奇怪，会觉得枚举7/8和枚举6/7，这两个7是不是重复了？你如果单看那种能被7整除的数，那么当然是重复的，如果是那些不能被7整除的数，那么和7搭配的6/8就是两种不同组合方式

那么我们如何判断一个数y能否由x/x+1这两个数组合而成呢？即y=ax+b(x+1)，要求a+b的值尽可能小(如果数学好，这题也已经被秒了，本质就是exgcd)，如果数学不好，怎么办？

我们来想一想，如果我们要让分配的每个组的个数相差为1，其实就是让y平均分配到每组(注意这里的平均要求分出的组的个数最少)，我们先用y/(x+1)得到n组，剩下m=y%(x+1)个，如果m+n>=x，那么我们可以从n中的m组各自拿出一个1，使得剩下的元素个数也符合条件，这样就能得到最少的分配组数，而如果m+n<x，显然这是不符合条件的

那么这时有人就会有另一个想法：如果我们先用y/x得到n组，剩余m=y/x个，如果m<=n就符合条件，如果m>n就不符合条件，是不是也行呢？看似和上面的想法很契合，很相似，但是这是不行的，不信可以去写一下代码试试，你会在[10,10,10,3,1,1]这个样例挂掉，这里简单说明一下原因，这n/k不能保证是最小分组，因为我们是每次的分组方案是k/k+1，你用n/k的结果其实和n/(k+1)天差地别，如果n=20，k=4，用n/k得到最小分组数为5，但是n/(k+1)的最小分组数却是4，更别说n更大了，只会相差越来越多，这里本质还是没有明白上面绿色的句子，即怎么平均才能让分出的组的个数尽可能的少？好好理解一下

代码如下

class Solution {
public:
    int minGroupsForValidAssignment(vector<int>& nums) {
        unordered_map<int,int>cnt;
        int m=INT_MAX;
        for(auto& e:nums) cnt[e]++;
        if(cnt.size()==1) return 1;
        for(auto&[a,c]:cnt) m=min(m,c);
        int ans=INT_MAX;
        function<bool(int)>check=[&](int k)->bool{
            int res=0;
            for(auto&[a,c]:cnt){
                int mod=c%(k+1);
                int x=c/(k+1);
                if(mod==0)
                    res+=x;
                else if(k<=mod+x)
                    res=res+x+1;
                else
                    return false;
            }
            ans=min(ans,res);
            return true;
        };
        
        for(int i=m;i>=1;i--){
            if(check(i))
                break;
        }
        return ans;
    }
};

四、得到k个半回文串的最小修改次数

这题主要是概念比较唬人，这个半回文串估计很多人都看蒙了，这里建议结合样例多手玩一下，基本上就懂了，这里就不对这个概念做深入讨论了，这里提醒一下，子串的长度>=2

这题其实不复杂，只要预处理一下每个数的真因子和每个子串变成半回文串需要修改的最小字符数，然后一个动态规划看看怎么划分子串就行了，关键是你能不能将思路写成代码

//预处理出每个数的真因子
int MX=201;
vector<vector<int>>v(MX);
int init=[](){
    for(int i=1;i<MX;i++)
        for(int j=2*i;j<MX;j+=i)
            v[j].push_back(i);
    return 0;
}();
class Solution {
public:
    //计算每个子串变成半回文串的需要修改的最小字符数
    int get_min(const string& s){
        int n=s.size();
        int res=n;
        for(int d:v[n]){//枚举因子进行划分
            int m=0;
            for(int j=0;j<d;j++){//枚举每一个子序列
                for(int l=j,r=n-d+j;l<r;l+=d,r-=d){//计算每个子序列变成回文串需要修改的字符数
                    m+=(s[l]!=s[r]);
                }
            }
            res=min(res,m);
        }
        return res;
    }

    int minimumChanges(string s, int k) {
        int n=s.size();
        vector<vector<int>>modify(n,vector<int>(n));
        //计算每个子串的最小修改次数
        for(int l=0;l<n-1;l++){
            for(int r=l+1;r<n;r++){
                modify[l][r]=get_min(s.substr(l,r-l+1));
            }
        }

        vector<vector<int>>memo(n,vector<int>(k,n+1));//n+1代表没有计算过，因为字符串最多只有n个元素，不可能需要修改n+1次
        function<int(int,int)>dfs=[&](int r,int k)->int{
            if(k==0) return modify[0][r];
            if(memo[r][k]<=n) return memo[r][k];
            int res=INT_MAX;
            for(int l=r-1;l>=2*k;l--){
                res=min(res,dfs(l-1,k-1)+modify[l][r]);
            }
            return memo[r][k]=res;
        };
        return dfs(n-1,k-1);
        
        //动态规划
        //vector<vector<int>>dp(k,vector<int>(n));
        //dp[0]=modify[0];
        //for(int i=1;i<k;i++){
        //    for(int r=2*i+1;r<n;r++){
        //        int res=INT_MAX;
        //        for(int l=r-1;l>=2*i;l--){
        //            res=min(res,dp[i-1][l-1]+modify[l][r]);
        //        }
        //        dp[i][r]=res;
        //    }
        //}
        //return dp[k-1][n-1];
    }
};