前言

本篇文章讲解C语言的数据结构中，时间复杂度、空间复杂度的定义，以及例题说明。
详细介绍了大O渐进法和如何计算一个代码的时间复杂度和空间复杂度。最后还有一个以空间复杂度换取时间复杂度的思想。

---

1.时间复杂度

1.1 时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

1.2 大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

常见复杂度举例：

数	复杂度
5201314	O(1)
3n+4	O(n)
3n2+4n+5	O(n2)
2n	O(2n)

1.3 常见时间复杂度计算举例

1.3.1 例1

计算Func2的时间复杂度？

void Func2(int N)
{
  int count = 0;
  for (int k = 0; k < 2 * N ; ++ k)
  {
   ++count;
  }
  int M = 10;
  while (M--)
  {
   ++count;
  }
  printf("%d\n", count);
}

基本操作执行了2N+10次(for循环2N次，while循环10次)，通过推导大O阶方法知道，时间复杂度为 O(N)

1.3.2 例2

计算Func4的时间复杂度？

void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}

实例3基本操作执行了100次，通过推导大O阶方法，时间复杂度为 O(1)

1.3.3 例3

计算strchr的时间复杂度？

const char * strchr ( const char * str, int character );
while(*str)
{
  if(*str==character)
    return str;
    ++str;
}

有可能在开始就找到了，有可能在中间找到，还有可能到最后才找到。
基本操作执行最好1次，最坏N次，时间复杂度一般看最坏，时间复杂度为 O(N)

1.3.4 例4

计算BubbleSort的时间复杂度？

void BubbleSort(int* a, int n)
{
  assert(a);
  for (size_t end = n; end > 0; --end)
  {
    int exchange = 0;
    for (size_t i = 1; i < end; ++i)
    {
      if (a[i-1] > a[i])
       {
        Swap(&a[i-1], &a[i]);
        exchange = 1;
       }
    }
    if (exchange == 0)
     break;
  }
}

end开始是n，第二个for循环内部是n-1，n-2，…，2，1。
所以求和，首相加末项乘项数再除2，即n*(n-1)/2，即时间复杂度为O(n²)

提示：计算时间复杂度的适合千万不能数代码中循环，不能看见两个循环就写O(n2),一定要根据思想来灵活计算。

1.3.5 例5

计算BinarySearch的时间复杂度？

int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
// [begin, end]：begin和end是左闭右闭区间，因此有=号
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}

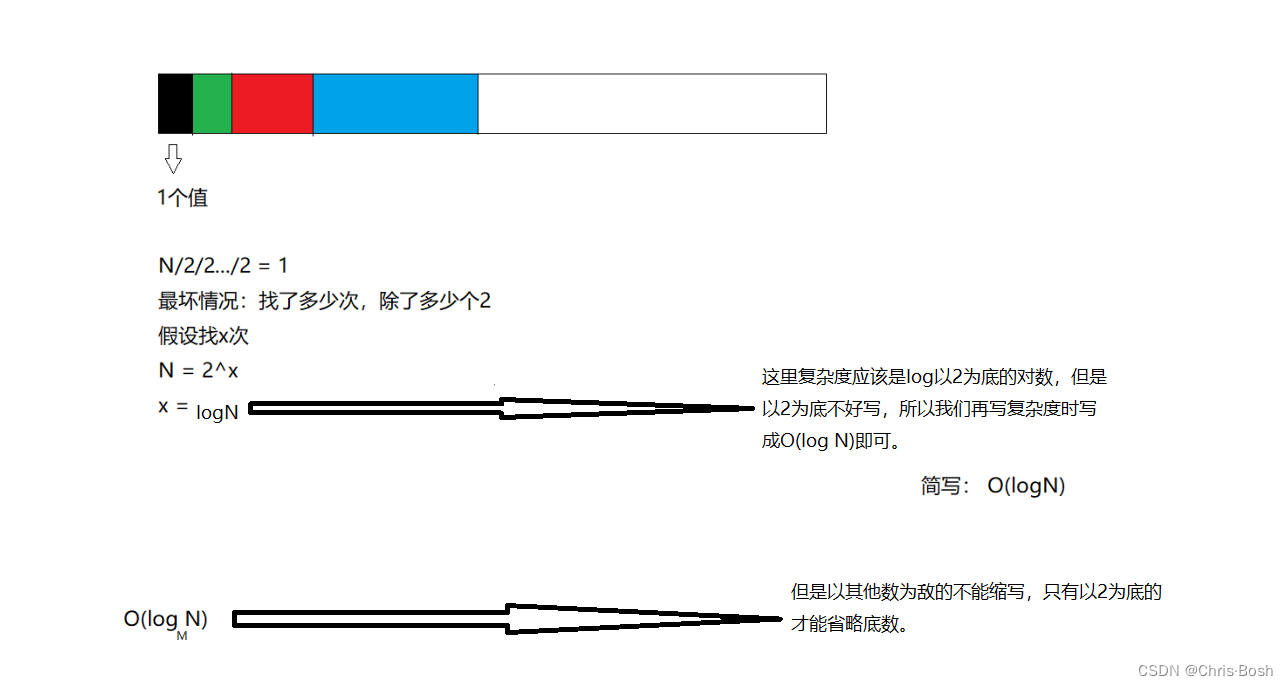
这是一个二分查找

1.3.6 例6

计算阶乘递归Fac的时间复杂度？

long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}

其从Fac(N)调用Fac(N-1)，再调用Fac(N-2)，…,一直调用到Fac(1)，Fac(0)
递归调用是多次调用累加，是次数的累加，不是累乘，有N次调用
所以时间复杂度是O(N)，千万不敢算成阶乘！！

1.3.7 例7

计算斐波那契递归Fib的时间复杂度？

long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}

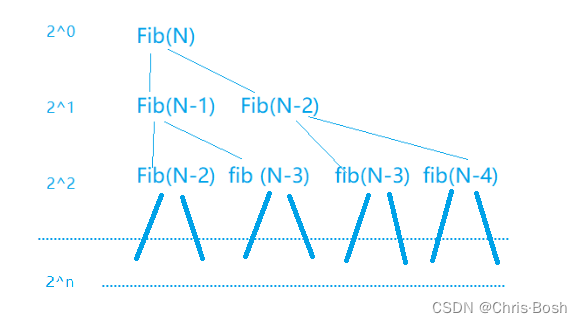
这是一个等比数列求和的思想
N < 3时递归结束，所以其最多到n-2.> 再利用等比数列求和的错为相减计算。 计算分析发现基本操作递归了2^N次，时间复杂度为O(2^N)。
如果真的有人按照错位相减算出来了，发现结果应该是2^(n-1)-2⁰,但是时间复杂度是一个估算，取O(2^N)。

2.空间复杂度

2.1 空间复杂度的概念

①空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时额外占用存储空间大小的量度 。
②空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

2.2 常见空间复杂度计算举例

2.3.1 例1

计算BubbleSort的空间复杂度？

void BubbleSort(int* a, int n)
{
  assert(a);
  for (size_t end = n; end > 0; --end)
  {
    int exchange = 0;
    for (size_t i = 1; i < end; ++i)
    {
      if (a[i-1] > a[i])
       {
        Swap(&a[i-1], &a[i]);
        exchange = 1;
       }
    }
    if (exchange == 0)
     break;
  }
}

进行冒泡排序，这个数组不是排序的消耗，只是有一个数组存值，所以数组不算空间复杂度。
其他只有少量新开辟的量，如exchange，end等，因此空间复杂度为O(1)。

2.3.2 例2

计算Fibonacci的空间复杂度？

long long* Fibonacci(size_t n)
{
    if(n==0)
    return NULL;
    long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
    fibArray[0] = 0;
    fibArray[1] = 1;
     for (int i = 2; i <= n ; ++i)
     {
       fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
     }
    return fibArray;
}

malloc开辟了新空间，开辟了一个(n+1)的数组 。与上面例1相比，这个数组不是存值，是想解决问题额外开的数组。
这时候空间复杂度为O(n)。

2.3.3 例3

计算阶乘递归Fac的空间复杂度？

long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}

递归的空间复杂度计算，也是空间累加，但是不同的是空间可以重复利用。
一个Fac调用一个Fac，一共N个，所以空间复杂度是O(N).

2.3.4 例4

计算斐波那契递归Fib的空间复杂度？

long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}

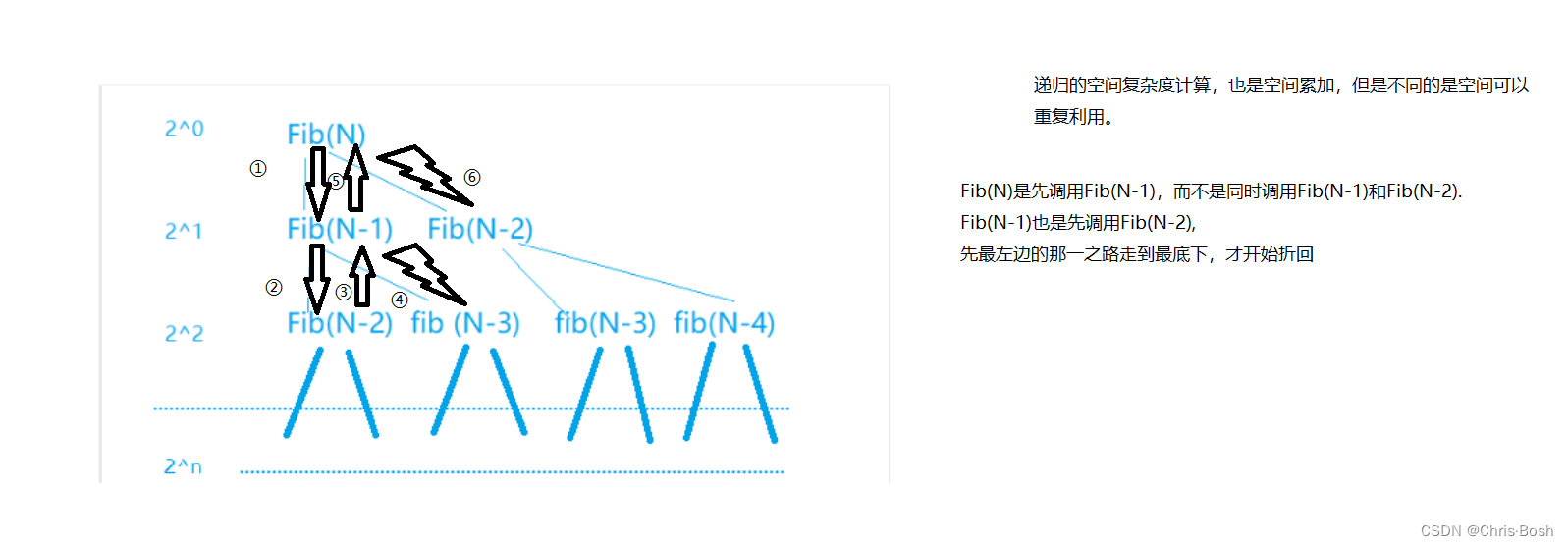
所以这里本质上也是一个斐波那契额调用一个斐波那契,空间复杂度为O(N)。

3.用空间复杂度换取时间复杂度的思想

以此题为例：

这两个思路的时间复杂度较大，我们想利用空间复杂度换取时间复杂度

思想如下：