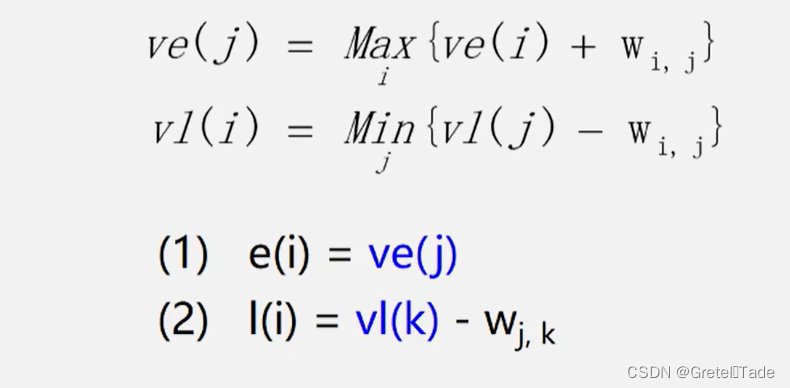目录
前言
AOE网
1.基本概念
2.应用
关键路径
1.算法理论
2.代码实现（C/C++）
前言
前面学习了图AOV网的应用，即拓扑排序，那这一期我们学习AOE网的应用，这是一个图的一个很广泛问题，也就是关键路径。那什么是关键路径呢？下面就一起来看看。
AOE网
1.基本概念
把工程计划表示为边表示活动的网络，即AOE网用顶点表示事件，弧表示活动，弧的权表示活动持续时间。
事件表示在它之前的活动已经完成，在它之后的活动可以开始
如图所示，这就是一个AOE网的问题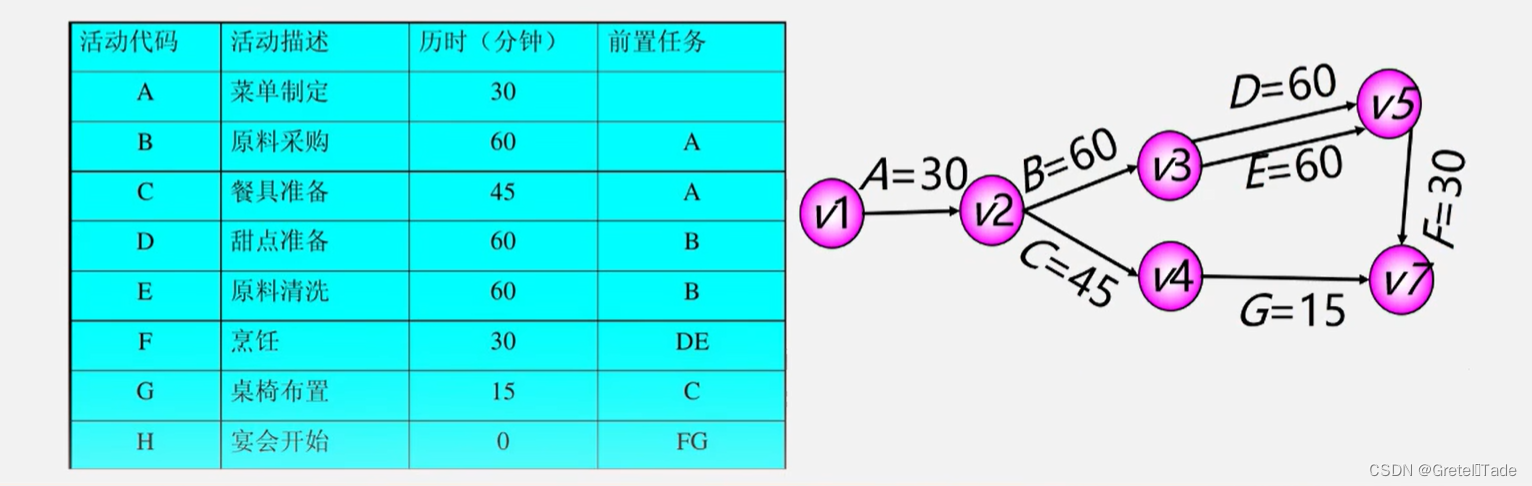
任意应该AOE网都有一个起点和终点，那这里就称作为源点和汇点。
源点与汇点
源点：入度为0的点，表示一个工程的开始。
汇点：出度为0的点，表示一个工程的结束。
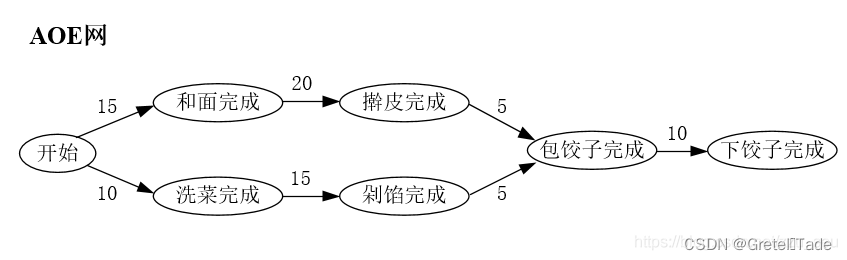
2.应用
对于AOE网，我们关心两个问题
- 完成整项工程至少需要多少时间？
- 哪些活动是影响工程进度的关键?
AOE网可以很好的表示一项工程或者项目经历的流程和时间，那现在提出一个问题：如何从起点到终点经历过的总时间最长呢？（完成这个工程需要的最长时间）
这里就要用到关键路径的算法了，下面我们就来看看关键路径是怎么q求的。
关键路径
关键路路径-----路径长度最长的路径
路径长度------路径上各活动持续时间之和。
1.算法理论
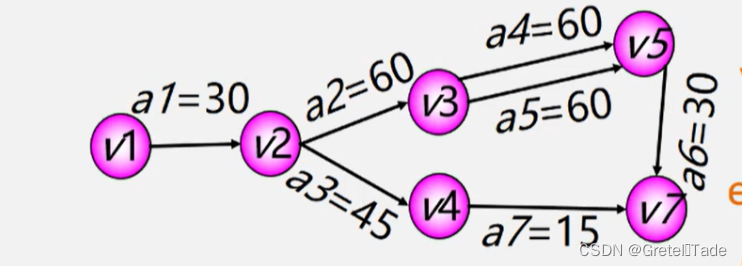以这个图为示例，下面要弄懂4个数组数据的值
1. ve(vj)------表示事件 vj的最早发生时间
例: ve(v1) = 0 ve(v2) = 30
2.vl(vj)-----表示事件 vj 的最迟发生时间
例: vl(v4) = 165
3.e(i)-----表示活动ai的最早开始时间
例：e(a3) = 30
4.l(i)-----表示活动ai 的最迟开始时间
例: l(a3) = 120
l(i) - e(i)-表示完成活动 ai 的时间余量。 例: (3) - e(3) = 90
关键活动
关键活动关键路径上的活动，即 l(i) == e(i) (即 l(i) - e(i) ==0 ) 的活动
以上4个量的关系：
1.如何找l)== e(i)的关键活动?
设活动 ai 用弧 <j,k> 表示，其持续时间记为: Wj,k
则有: (1) e(i) = ve(j)
(2) l(i) = vl(k) - Wj, k
2.如何求 ve(j)和 vl(j) ?
(1) 从 ve(1)=0开始向前递推
ve(j) = Max{ve(i) + Wij}, < i,j >属于T, 2 <=j <=n
其中T是所有以i为头的弧的集合。
(2)从 vl(n)= ve(n)开始向后递推
vl(i) = Min{vl(j) - Wij}, < i, j >属于S, 1<=i<=n -1
其中 S 是所有以i为尾的弧的集合。
注意：最短路径与最小生成树不同，路径上不一定包含 n个顶点，也不定包含 n-1条边
求解过程，以下图为案例求解ve、vl、e、和l数组。
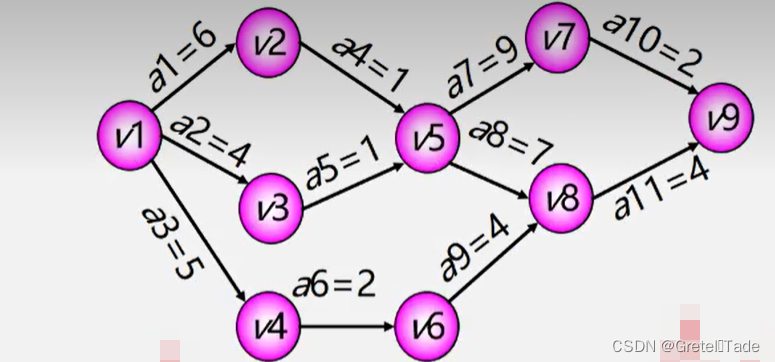
求关键路径步骤:
- 求 ve(i)、vl(j)
- 求e(i)、l(i)
- 计算 l(i) - e(i)，如果值为0那就是关键路径中的一条路径
- 套用以下公式即可
求得的ve和vl如图所示：
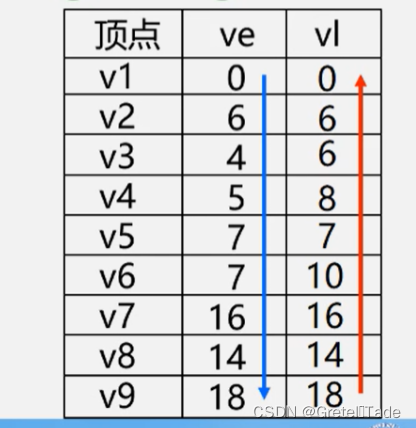
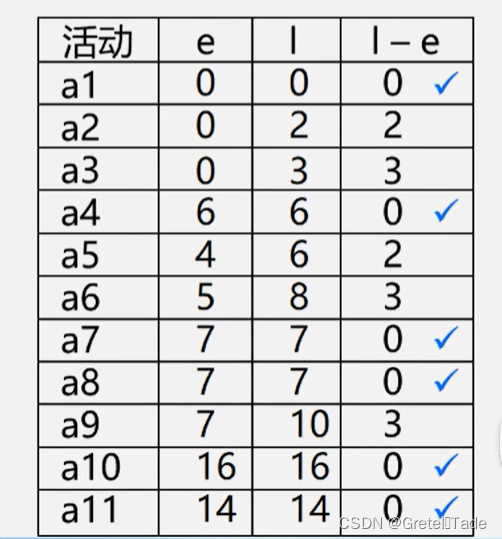
求得的e和l，如图所示：
2.代码实现（C/C++）
邻接矩阵图的结构体：
#define Maxint 32767
#define Maxnum 100//最大顶点数
//数据类型
typedef struct datatype {
char id[10];
//……
}
ElemType;
//图的邻接数组
typedef struct graph {
ElemType vexs[Maxnum];//图数据
int matrix[Maxnum][Maxnum];//二维数组矩阵
int vexnum;//点数
int arcnum;//边数
}Graph;关键路径算法代码：
//获取入度为0的起始点下标
int in_degree0(Graph G) {
int* sum_degree = (int*)malloc(sizeof(int) * G.vexnum);
memset(sum_degree, 0, sizeof(int) * G.vexnum);
for (int x = 0; x < G.vexnum; x++) {
for (int y = 0; y < G.vexnum; y++) {
if (G.matrix[y][x] != 0 && G.matrix[y][x] != Maxint) {
sum_degree[x]++;
}
}
}
for (int i = 0; i < G.vexnum; i++) {
if (sum_degree[i] == 0) {
free(sum_degree);
sum_degree = NULL;
return i;
}
}
}
//获取出度为0的交汇点下标
int out_degree0(Graph G) {
int* sum_degree = (int*)malloc(sizeof(int) * G.vexnum);
memset(sum_degree, 0, sizeof(int) * G.vexnum);
for (int x = 0; x < G.vexnum; x++) {
for (int y = 0; y < G.vexnum; y++) {
if (G.matrix[x][y] != 0 && G.matrix[x][y] != Maxint) {
sum_degree[x]++;
}
}
}
for (int i = 0; i < G.vexnum; i++) {
if (sum_degree[i] == 0) {
free(sum_degree);
sum_degree = NULL;
return i;
}
}
}
//队列的结构体
typedef struct q {
int prev;//上一个顶点下标
int next;//下一个顶点下标
}Queue;
//边的结构体 起点 长度 终点
typedef struct e {
int begin_index;//这个边的起始点
int e;//边长度
int end_index;//这个边的终点
}E;
//关键路径算法AOE
void Critical_path(Graph G) {
//申请ve,vl,e,l的空间
int* ve = (int*)malloc(sizeof(int) * G.vexnum);
int* vl = (int*)malloc(sizeof(int) * G.vexnum);
E* e = (E*)malloc(sizeof(E) * G.arcnum);
int* l = (int*)malloc(sizeof(int) * G.arcnum);
Queue* queue = (Queue*)malloc(sizeof(Queue) * G.vexnum);
//01--处理ve
for (int k = 0; k < G.vexnum; k++) {
queue[k].prev = queue[k].next = -1;
ve[k] = 0;
}
//对第一个数据处理
int begin = in_degree0(G);
//初始化
int qu_count = 0;
queue[qu_count].prev = queue[qu_count].next = begin;
qu_count++;
//后继处理
while (qu_count) {
//出队操作
Queue pop = queue[0];
//后继数据前移
for (int d = 0; d < qu_count - 1; d++) {
queue[d] = queue[d + 1];
}
qu_count--;
//获取到出队顶点最早开始时间ve
int max = ve[pop.prev] + G.matrix[pop.prev][pop.next];
if (ve[pop.next] <= max)
ve[pop.next] = max;
//把当前出队的顶点后继连接的顶点入队
for (int j = 0; j < G.vexnum; j++) {
if (G.matrix[pop.next][j] != 0 && G.matrix[pop.next][j] != Maxint) {
queue[qu_count].next = j;
queue[qu_count].prev = pop.next;
qu_count++;
}
}
}
//02--处理vl
int end = out_degree0(G);
for (int k = 0; k < G.vexnum; k++) {
queue[k].prev = queue[k].next = -1;
vl[k] = ve[end];
}
//对第一个数据处理
queue[qu_count].next = queue[qu_count].prev = end;
qu_count++;
while (qu_count) {
//出队
Queue pop = queue[0];
//后继数据前移
for (int d = 0; d < qu_count - 1; d++) {
queue[d] = queue[d + 1];
}
qu_count--;
//比较找到最小值赋予到vl
int min = vl[pop.next] - G.matrix[pop.prev][pop.next];
if (min <= vl[pop.prev])
vl[pop.prev] = min;
//把当前出队的顶点前面相连的顶点入队
for (int i = 0; i < G.vexnum; i++) {
if (G.matrix[i][pop.prev] != 0 && G.matrix[i][pop.prev] != Maxint) {
queue[qu_count].prev = i;
queue[qu_count].next = pop.prev;
qu_count++;
}
}
}
//03--处理e
int e_count = 0;
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++) {
if (G.matrix[i][j] != 0 && G.matrix[i][j] != Maxint) {
e[e_count].begin_index = i;
e[e_count].e = ve[i];//套用公式
e[e_count].end_index = j;
e_count++;
}
}
}
//04--处理l
int l_count = 0;
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++) {
if (G.matrix[i][j] != 0 && G.matrix[i][j] != Maxint) {
//套用公式
l[l_count++] = vl[j] - G.matrix[i][j];
}
}
}
//输出结果
printf("\nve数组结果：");
for (int j = 0; j < G.vexnum; j++) {
printf("%d ", ve[j]);
}
printf("\nvl数组结果：");
for (int j = 0; j < G.vexnum; j++) {
printf("%d ", vl[j]);
}
printf("\ne的结果：");
for (int j = 0; j < G.arcnum; j++) {
printf("%d ", e[j].e);
}
printf("\nl的结果：");
for (int j = 0; j < G.arcnum; j++) {
printf("%d ", l[j]);
}
printf("\n关键路径路线如下：\n");
for (int j = 0; j < G.arcnum; j++) {
if (e[j].e - l[j] == 0) {
int start = e[j].begin_index;
int end = e[j].end_index;
printf("%s->%s %d\n", G.vexs[start].id, G.vexs[end].id, G.matrix[start][end]);
}
}
//释放空间
free(ve);
free(vl);
free(e);
free(l);
free(queue);
ve = vl = e = l = queue = NULL;
}
测试结果：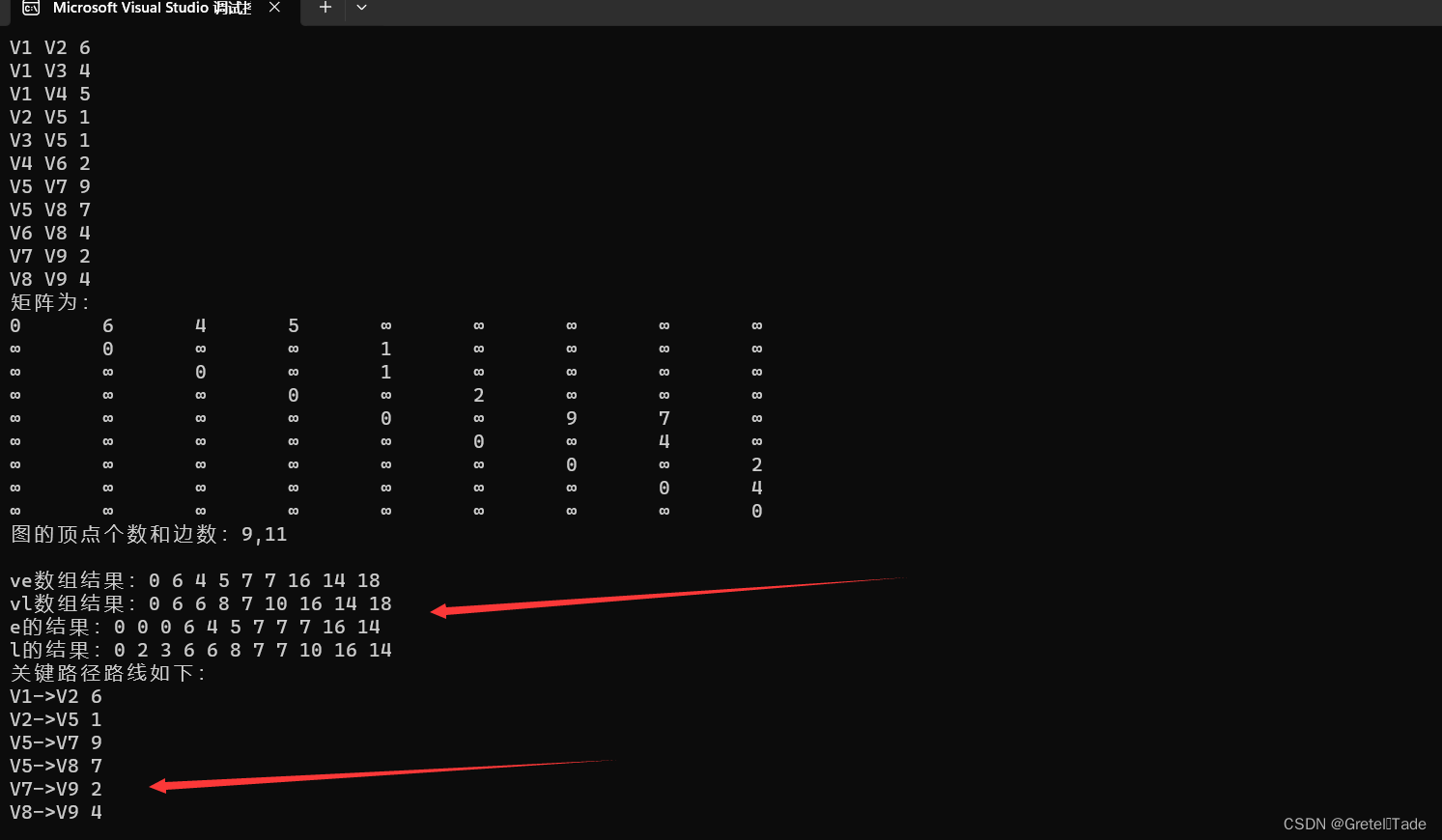
以上就是本期的内容了，喜欢的话点个赞吧！
分享一张壁纸：
