---

一、前缀和

前缀和问题

前缀和用来快速解决某一段连续区间的和。

时间复杂度O(1)

注意：不要背模板，不要背模板，不要背模板！！！

一维前缀和模板

• 1）预处理一个前缀和数组

• • 针对本道题：前缀和模板
• • dp[i] = dp[i-1] + arr[i];
    dp[i]表示：从[1,i]连续区间内所有元素的和。

• 2）使用前缀和解决问题

---

重点：不要背模板，不要背模板，不要背模板！！！

每道题的情况不同，唯一相同的是前缀和思想，利用这个思想求一段连续区间内所有元素的和即可。

二维前缀和模板

二维前缀和

以该题为例：

利用二维前缀和数组的思想：
dp[i][j]表示：从[1,1]坐标开始到[i,j]坐标结束，这段连续区间内所有元素的和。

dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1]

细节处理

由于i应该要从1开始，所以当i = 0时，会越界，这里可以多开一个空间，并保证空间的初始化不会影响后续的结果。

题目1

寻找数组的中心下标

思路

使用一维前缀和的思想，假设
[0~i-1]区间的所有元素的和 = f[i];
[i+1,n-1]区间的所有元素的和 = g[i];

f[i] = f[i-1] + arr[i-1];
g[i] = g[i+1] + arr[i+1];

细节处理：

• f[0] = 0,g[n-1] = 0
  因为这种边界情况会越界
  f从左到右开始求和
  g从右到左求和

题目2

除自身以外数组的乘积

思路

与题目一思路几乎一样。

题目3

和为 K 的子数组

这道题上强度了，难度比较大，我是看了解析看了三遍才弄懂它的思路。

题目4

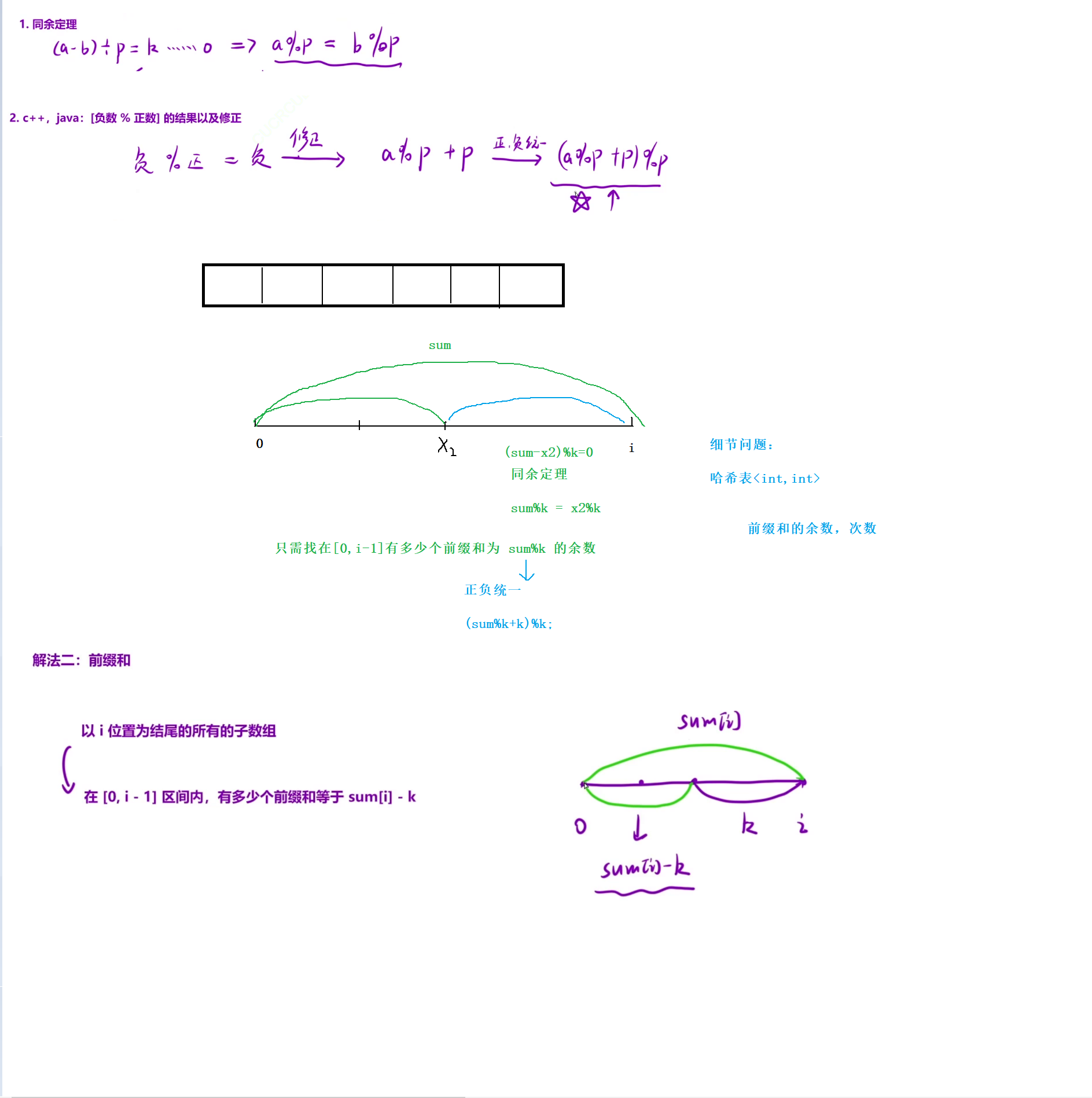
和可被 K 整除的子数组

这道题的整体思路与上一道题的思路也是几乎相同。

主要区别就是这道题要引入一个数学定理。

还有一个在c++和java两个语言中，负%正=负；这个问题在本道题中需要进行修正。

其他细节问题一样的。

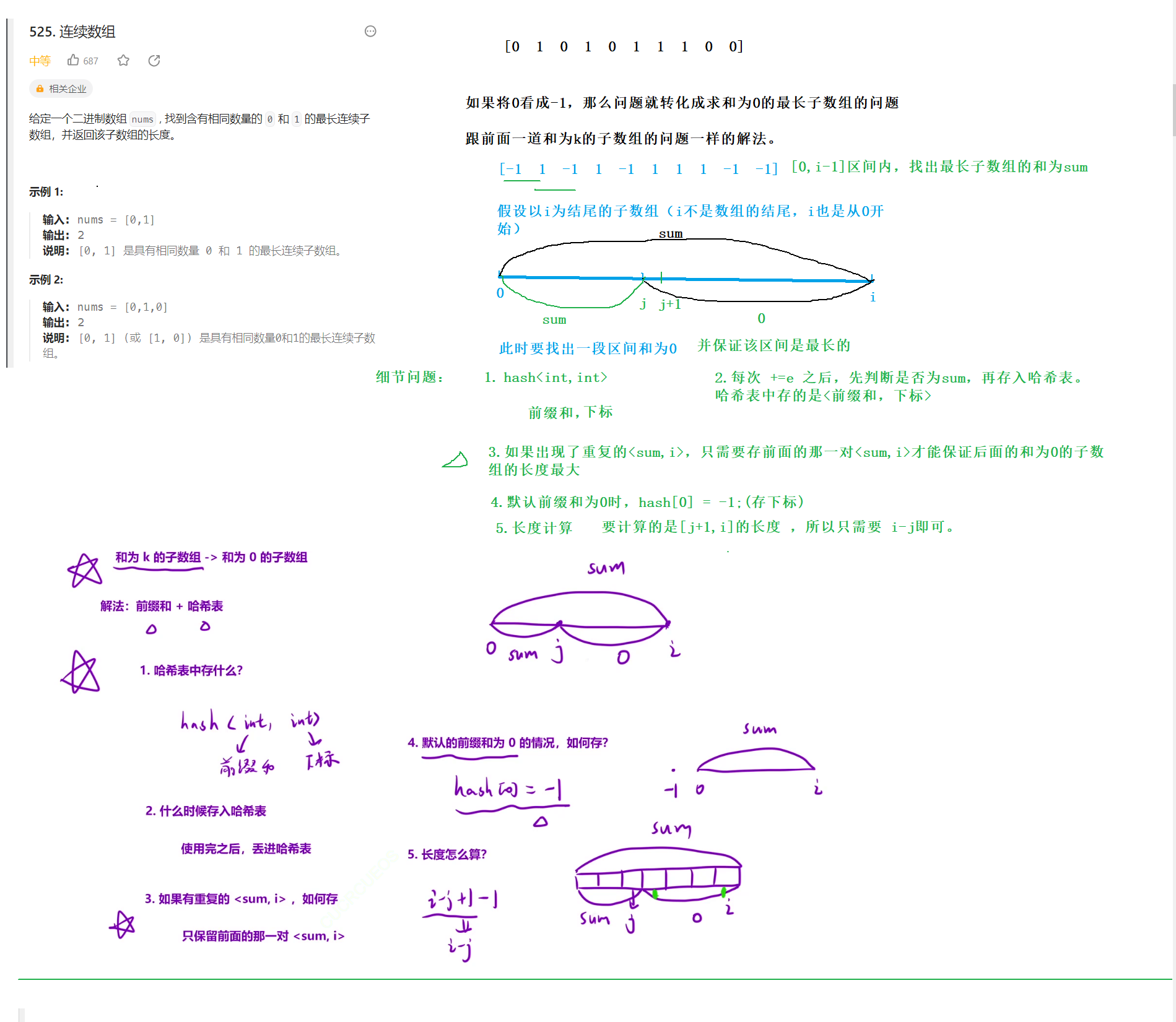
题目5

连续数组

解题思路：

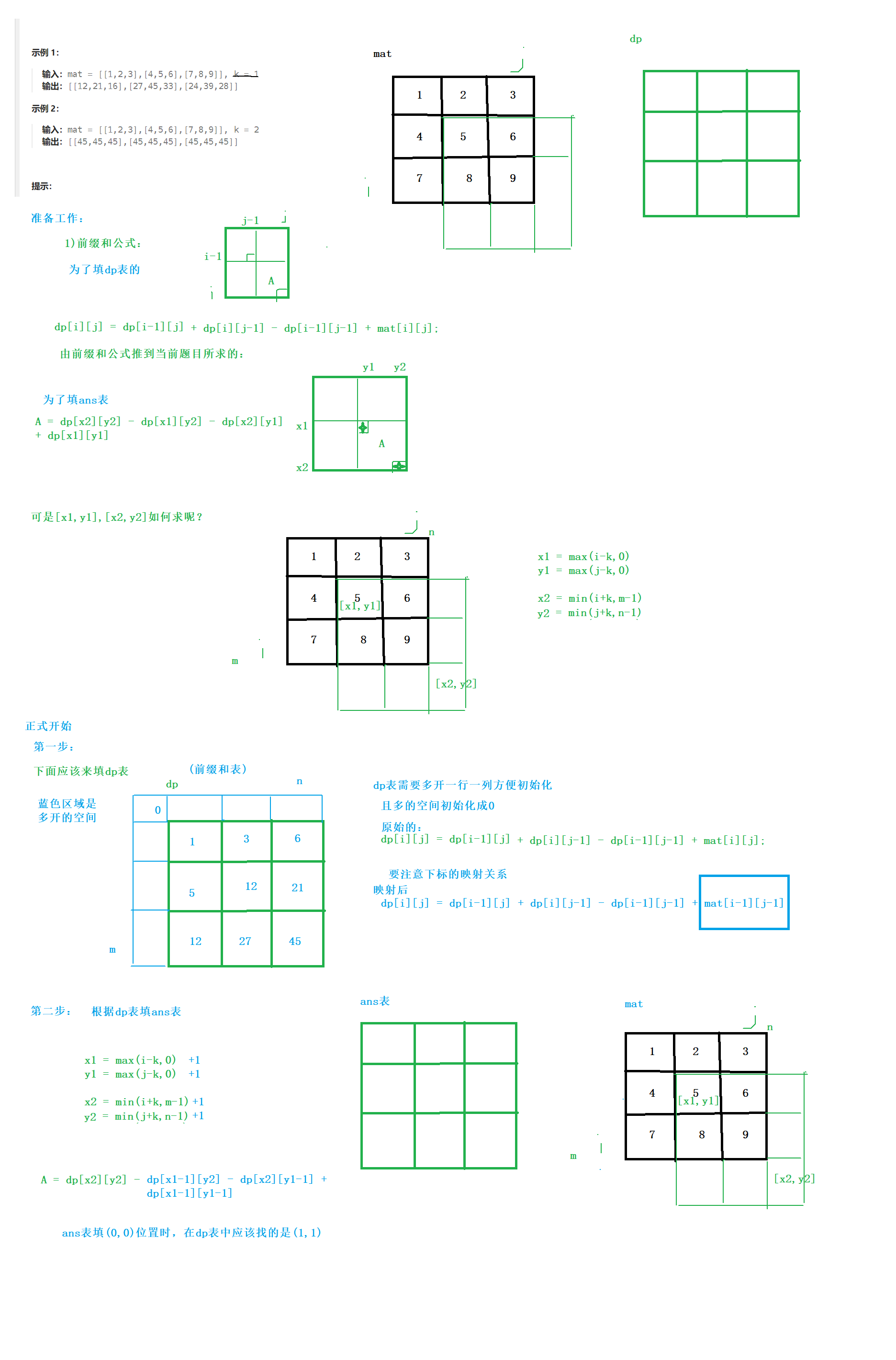
题目6

矩阵区域和

这道题是一个二维前缀和，难度还是挺大的，不过只要把思路捋清楚，多花点时间也是可以的。

---

总结

这篇文章是关于前缀和的题目解题思路以及一些模板，还是那句话，不要背模板。