2-1
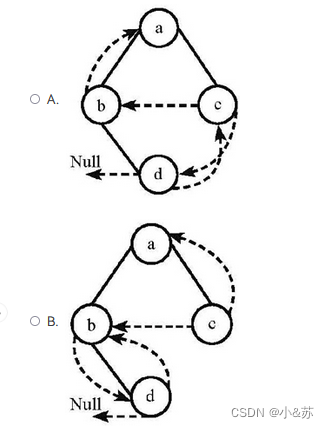
下列线索二叉树中（用虚线表示线索），符合后序线索树定义的是：B


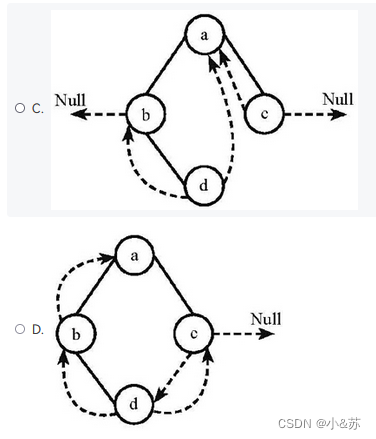
解析：
后序遍历dbca 所以d前驱为null，d后继为b，c没有孩子，前驱为b，后继为a，a有左右孩子。

2-2
引人线索二叉树的目的的是（ ）。 (2分)

A.加快查找结点的前驱或后继的速度
B.为了能在二叉树中方便地进行插人与侧除
C.为了能方便地找到双亲
D.使二叉树的遍历结果唯一
解析：
以二叉链表作为存储结构时，只能得到结点的左右孩子信息，结点的任意序列中的前驱和后继信息只能在遍历的动态过程中才能得到，为了查找结点的前驱或后继，引入线索二叉树。

2-3
若X是后序线索二叉树中的叶结点，且X存在左兄弟结点Y，则X的右线索指向的是（　）。

A.X的父结点
B.以Y为根的子树的最左下结点
C.X的左兄弟结点Y
D.以Y为根的子树的最右下结点

解析：
根据后续线索二叉树的定义，x结点为叶子节点且有左兄弟，那么该节点为右孩子，通过后序遍历线索的方式可知，x节点的后继为其父节点，也即x的右线索指向的是x的父节点。

2-4
已知字符集{ a, b, c, d, e, f }，若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 }，则对应字符集中各字符的哈夫曼编码可能是：

A.00, 1011, 01, 1010, 11, 100
B.00, 100, 110, 000, 0010, 01
C.10, 1011, 11, 0011, 00, 010
D.0011, 10, 11, 0010, 01, 000
解析：

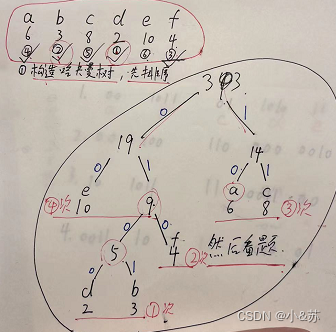
2-5
对 n 个互不相同的符号进行哈夫曼编码。若生成的哈夫曼树共有 115 个结点，则 n 的值是：

A.56
B.57
C.58
D.60

解析：
n=（115+1）/2=58

2-6
将森林转换为对应的二叉树，若在二叉树中，结点u是结点v的父结点的父结点，则在原来的森林中，u和v可能具有的关系是：

1 父子关系； 2. 兄弟关系； 3. u的父结点与v的父结点是兄弟关系

A.只有2
B.1和2
C.1和3
D.1、2和3

解析：
在二叉树中，u、v的关系有四种，v是u的左儿子的左儿子，左儿子的右儿子，右儿子的左儿子，右儿子的右儿子。对应森林中二者的关系只能是兄弟、父子。

2-7
对于一个有N个结点、K条边的森林，共有几棵树？

A.N−K
B.N−K+1
C.N−K−1
D.不能确定
解析：
每个边涉及两个节点，只有根不消耗边，有几个根，有几个树，树=根=N-K

2-8
设森林F中有三棵树，第一、第二、第三棵树的结点个数分别为M1​，M2​和M3​。则与森林F对应的二叉树根结点的右子树上的结点个数是：

A.M1​
B.M1​+M2​
C.M2​+M3​
D.M3​

解析：
左子树应该是M1，那么右子树只能是M2+M3

2-9
由若干个二叉树组成的森林F中，叶结点总个数为N，度为2的结点总个数为M，则该集合中二叉树的个数为：

A.M−N
B.N−M
C.N−M−1
D.无法确定

解析：
节点只有度为2和3两种，一棵树中，度为2个数比叶子节点少一。
所以二叉树个数为 N-M

2-10
若森林F有15条边、25个结点，则F包含树的个数是：

A.8
B.9
C.10
D.11

解析：
在n个节点的树中有n-1条边，那么对于每棵树，其结点数比边数多1。题中的森林中的结点数比边数多10（25-15=10），显然共有10棵树。

2-11
给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为：

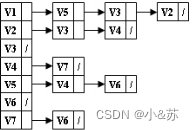
A.V1,V5,V4,V7,V6,V2,V3
B.V1,V2,V3,V4,V7,V6,V5
C.V1,V5,V4,V7,V6,V3,V2
D.V1,V5,V6,V4,V7,V2,V3

解析：
v1》v5》v4》v7》v6》v3》v2

2-12
下列选项中，不是下图深度优先搜索序列的是：

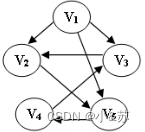
A.V1​, V5​, V4​, V3​, V2​
B.V1​, V3​, V2​, V5​, V4​
C.V1​, V2​, V5​, V4​, V3​
D.V1​, V2​, V3​, V4​, V5​

解析：
v2不能直接到v3

2-13
给定无向带权图如下，以下哪个是从顶点 a 出发深度优先搜索遍历该图的顶点序列（多个顶点可以选择时按字母序）？

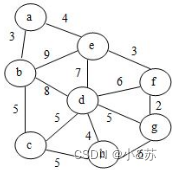
A.abecdfhg
B.abcdehgf
C.abcdefgh
D.abchgfde

解析：
只有c能通而且要按照字母顺序排序

2-14
如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则下列说法中不正确的是：

A.G肯定不是完全图
B.G中一定有回路
C.G一定不是连通图
D.G有2个连通分量
解析：
走两次才能访问所有节点，说明不是联通图

2-15
给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历，则得到的一种顶点序列为：

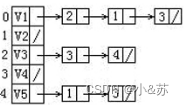
A.V1,V2,V3,V4,V5
B.V1,V2,V3,V5,V4
C.V1,V3,V2,V4,V5
D.V1,V4,V3,V5,V2
解析：
广度优先遍历，所以先走第一行。

2-16
已知一个图的邻接矩阵如下，则从顶点V1出发按广度优先搜索法进行遍历，可能得到的一种顶点序列为：

A.V1,V2,V3,V5,V4,V6
B.V1,V2,V4,V5,V6,V3
C.V1,V3,V5,V2,V4,V6
D.V1,V3,V5,V6,V4,V2
解析：
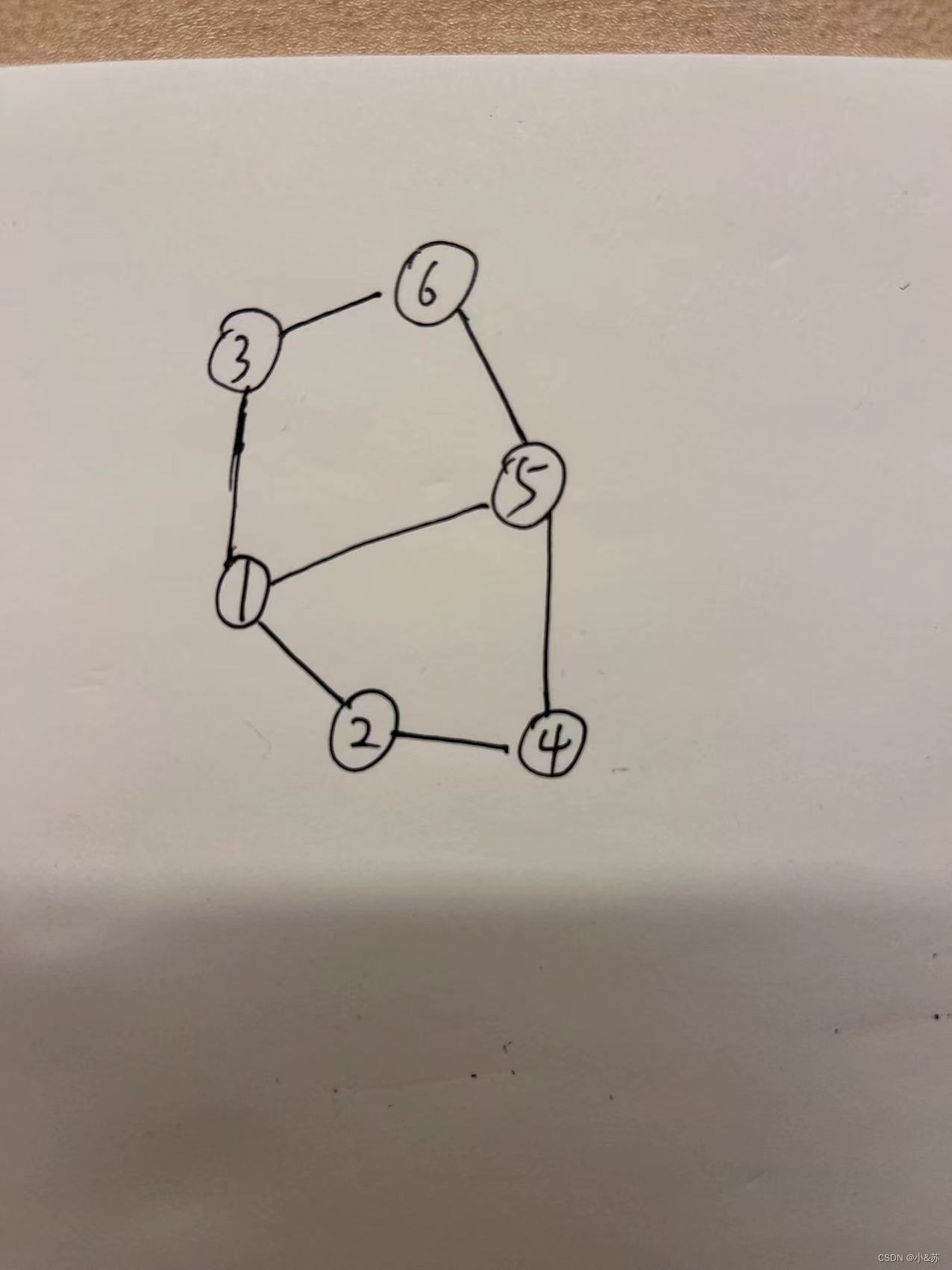层次遍历

2-17
图的广度优先遍历类似于二叉树的：

A.先序遍历
B.中序遍历
C.后序遍历
D.层次遍历

2-18

给定有权无向

图的邻接矩阵如下，其最小生成树的总权重是：

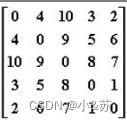
A.10
B.11
C.12
D.14
解析：

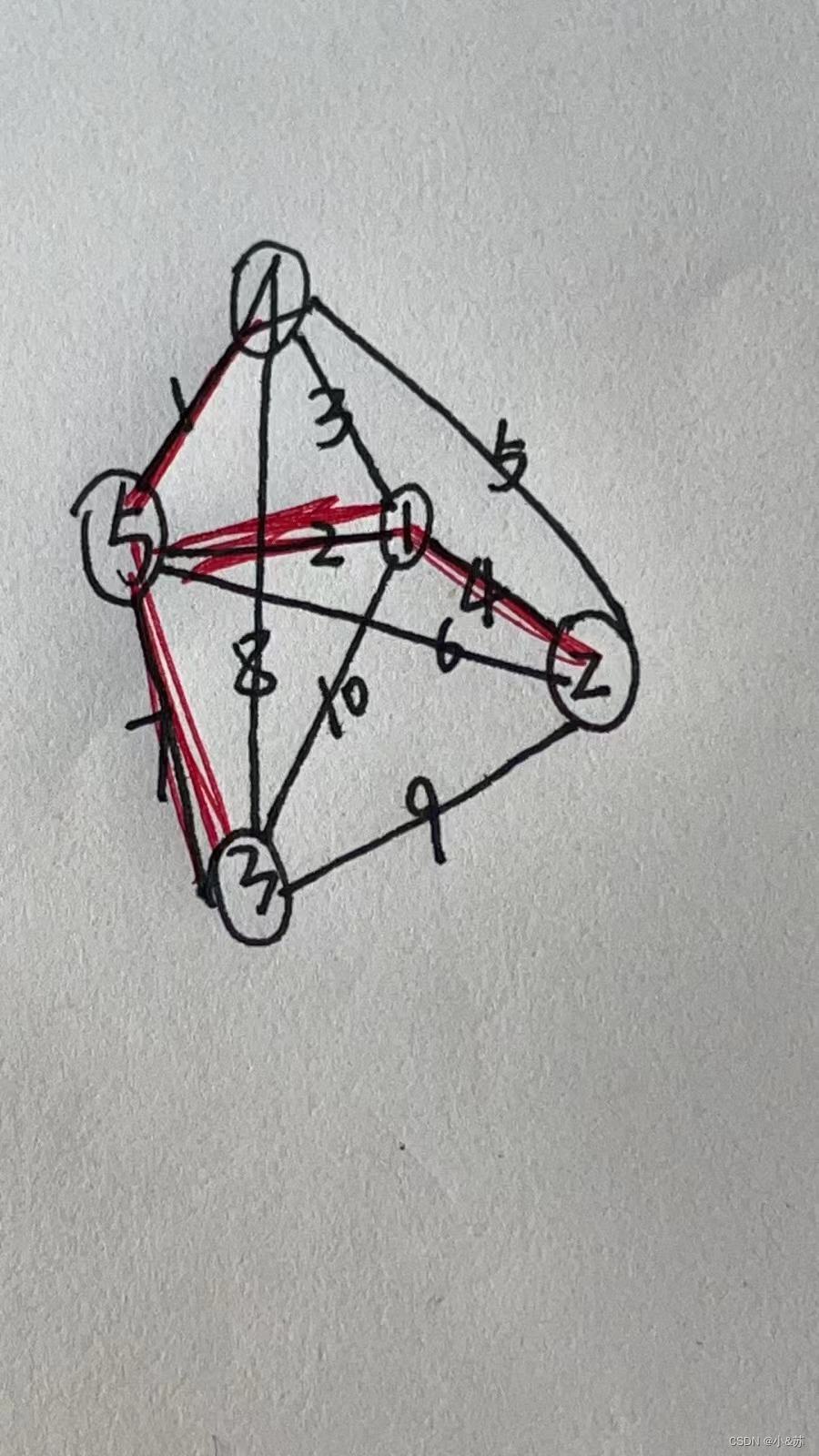
2-19
给定有权无向图的邻接矩阵如下，其最小生成树的总权重是：

A.20
B.22
C.8
D.15
解析：
画图可知
2-20
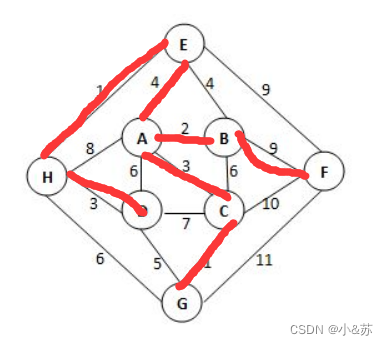
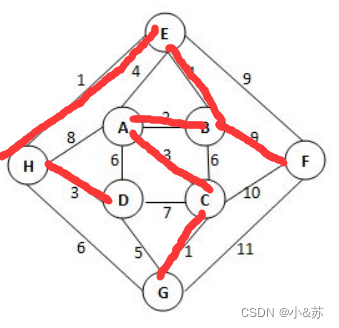
给定有权无向图如下。关于其最小生成树，下列哪句是对的？

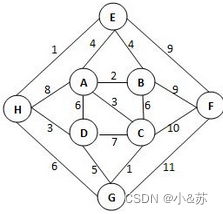
A.最小生成树不唯一，其总权重为23
B.最小生成树唯一，其总权重为20
C.边(B, F)一定在树中，树的总权重为23
D.边(H, G)一定在树中，树的总权重为20
解析：