电路综合-基于简化实频的SRFT微带线切比雪夫低通滤波器设计
0、基本理论
参考-Design of Ultra Wideband Power Transfer Networks的4.17小节的推导过程
n 次切比雪夫多项式定义为:
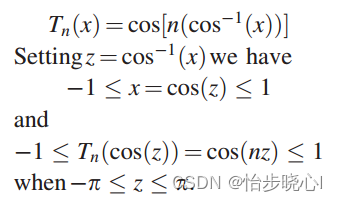
n在1到5时的切比雪夫多项式表:

此表可以使用下面的代码计算得出:
clear
clc
syms x
%定义切比雪夫阶数
n=1;
for n=1:1:9
T=(simplify(cos(n*acos(x))));
disp('----------------------------------------------------')
disp([num2str(n),'th Chebyshev polynomials is:']);disp(T);
end
代码的运行结果为:

下面介绍一些切比雪夫多项式的性质。
1、切比雪夫多项式的递归性质:

2、奇阶切比雪夫多项式在x=0时为0:
3、偶阶(阶数为2k)切比雪夫多项式在x=0时取值为±1:

4、切比雪夫多项式在x处于【-1,1】范围内的波动性:
在【-1,1】的范围之外,其特性由最高项2(n-1) xn决定。
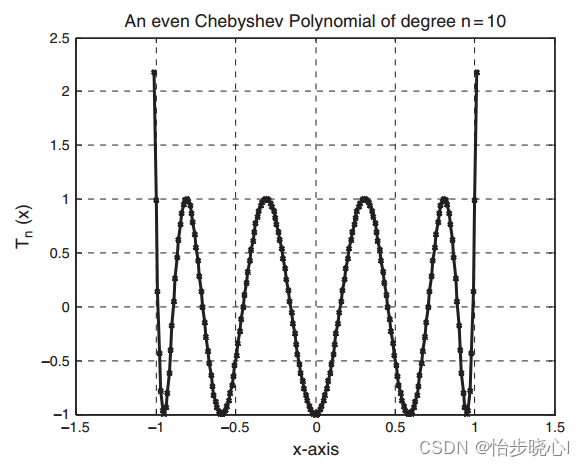
5、切比雪夫多的滚降增益函数与纹波因子:
定义
ε
2
{\varepsilon ^{\rm{2}}}
ε2为纹波因子,则切比雪夫多项式的增益函数
T
(
x
)
T(x)
T(x)可以写为(
T
n
(
x
)
{T_n}(x)
Tn(x)为切比雪夫多项式,区别于此处的增益函数
T
(
x
)
T(x)
T(x)):
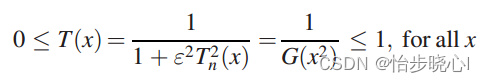
给出代码与结果进行直观展示:
clear
clc
close all
syms x
%定义切比雪夫阶数
n=5;
Tn=(simplify(cos(n*acos(x))));
disp('----------------------------------------------------')
disp([num2str(n),'th Chebyshev polynomials is:']);disp(Tn);
%定义纹波系数0.4
rr=0.4;
T=1/(1+rr*Tn*Tn);
figure
fplot(T)
title('纹波系数为0.4')
%定义纹波系数0.8
rr=0.8;
T=1/(1+rr*Tn*Tn);
figure
fplot(T)
title('纹波系数为0.8')
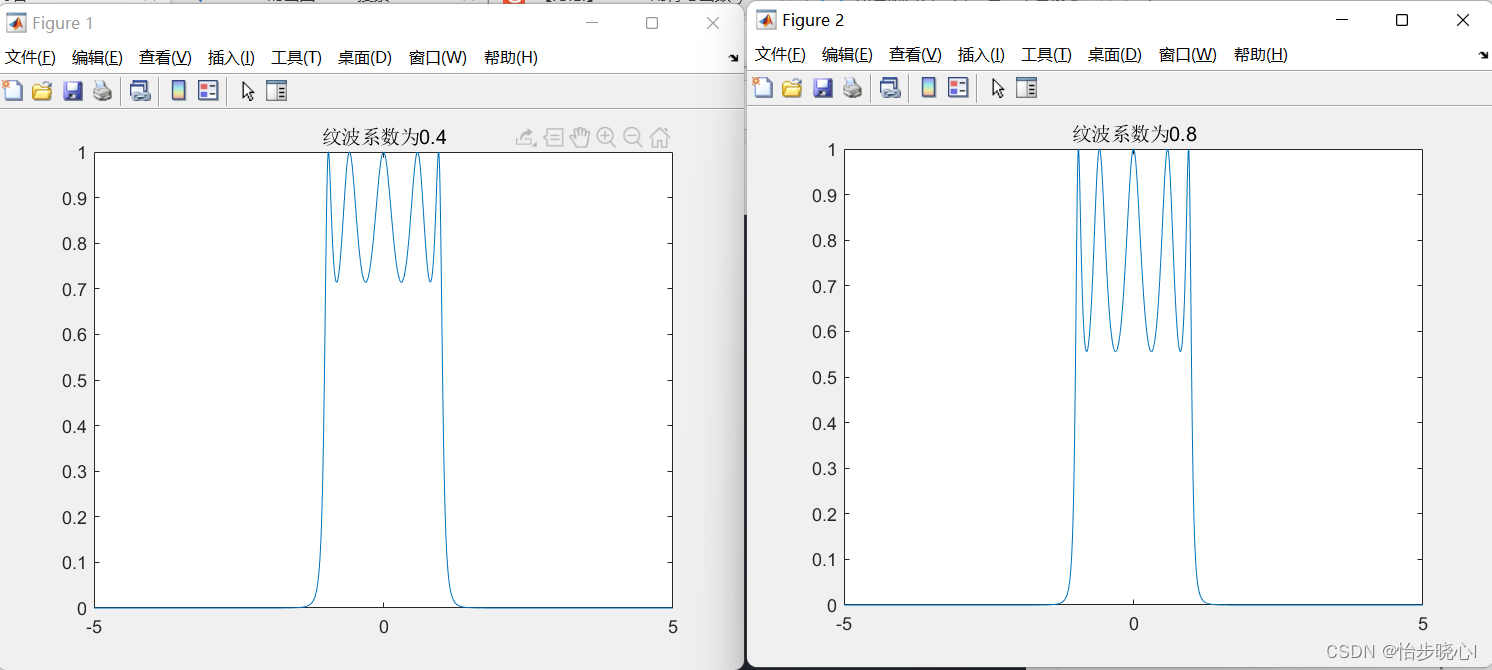
5、通带最大纹波(纹波因子并不直接代表通带的最大纹波):
通带纹波在
T
n
(
x
)
=
1
{T_n}(x)=1
Tn(x)=1时达到最大:
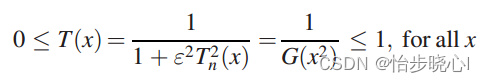
其
T
n
(
x
)
=
1
{T_n}(x)=1
Tn(x)=1的增益函数的计算表达式如下:
1
1
+
ε
2
\frac{1}{{1 + {\varepsilon ^2}}}
1+ε21
实际上通带波纹(单位dB)的计算公式如下:
10
log
10
(
1
+
ε
2
)
10{\log _{10}}(1 + {\varepsilon ^2})
10log10(1+ε2)
例如,要实现0.4dB的通带波纹,纹波因子可以使用如下的计算公式:
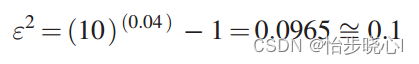
1、设计步骤理论
使用单调滚降切比雪夫增益函数设计低通微带线滤波器,微带滤波器截止频率为1GHz,通带波纹要小于0.4dB,阻带频率为3GHz,衰减量大于40dB。
STEP1:增益函数确定,就是用之前介绍的切比雪夫的增益函数:
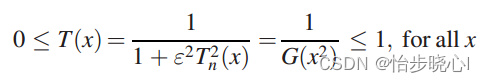
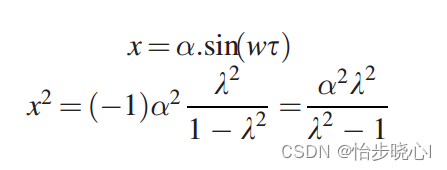
STEP2:确定纹波因子,使用之前理论介绍的公式即可,对于此处:
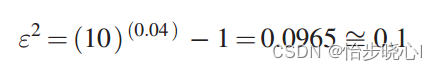
STEP3:确定单个微带线的传输延时(其中fe为截止频率,3GHz)
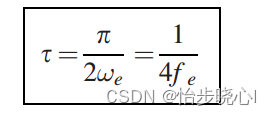
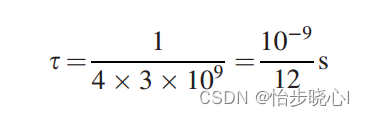
STEP4:确定ALPHA

STEP5:确定滤波器的阶数
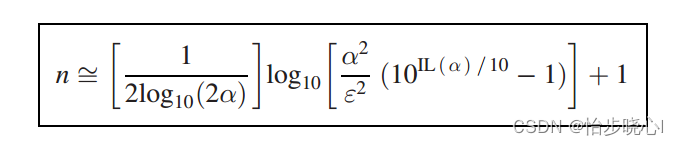
对于此处的设计,因为要实现阻带40dB的衰减,计算后得到所需的阶数为5
STEP6:生成功率传输函数TPG
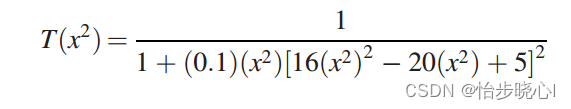
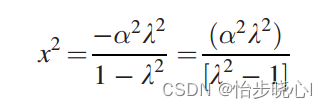
由此得到:
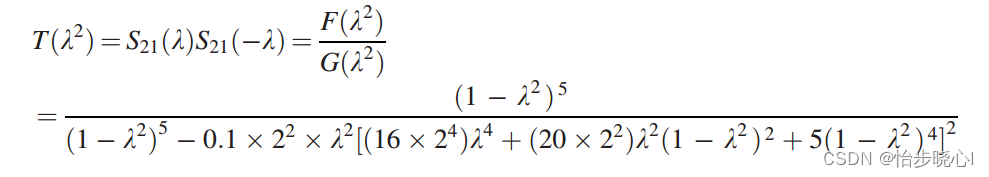
进而:

利用G和F可以求得S11或者Zin,进而可以使用5、电路综合-超酷-基于S11参数直接综合出微带线电路图中的方法得到实际的微带线电路图,下面也会介绍具体的步骤。
2、设计步骤实践
按照上述步骤编写代码(此处只展示主要代码,其余函数见文章开始的附件链接):
clear
clc
%通带截止频率
fc=1e9;
%阻带频率
fe=3e9;
%通带纹波,单位dB
ILR=0.4;
%阻带衰减,单位dB
IL=40;
% 计算纹波因子和角频率
eps_sq=10^(ILR/10)-1;
wc=2*pi*fc;
we=2*pi*fe;
% 计算传输延时tao
tau=pi/2/we;
% 计算alpha
alfa=1.0/(sin(pi*wc/we/2));
%计算所需的切比雪夫滤波器阶数
n=Cheby_Degree(IL,ILR,fc,fe);
%计算所需传输函数G和F
[F,G,g]=Denom_Cheby(n,eps_sq,alfa);
h =gtoh(F,G);
Z_imp=UE_sentez(h,g);
disp(['匹配使用的微带线的归一化特性阻抗为:',num2str(Z_imp(1:end-1))])
%使用在f Hz的电长度为ele_l的微带线进行实现
%光速
c=299792458;
%微带线电长度所在的频率
f=1e9;
%微带线电长度
ele_l=360*tau*f;
disp(['此处使用在',num2str(f/1e9),'GHz下电长度为',num2str(ele_l),'°的微带线进行实现']);
%求解频率范围,单位GHz
f_start=0.01;
f_stop=10;
f_step=0.01;
%求解范围
freq_solve=[f_start:f_step:f_stop]*1e9;
%计算物理长度,单位m
l=ele_l/360*c/f;
%计算不同频率下的相移常数beta
beta=2*pi*freq_solve/c;
%转换到lamda域
lamda=1j*tan(beta*l);
num_h=0;
for i=1:1:length(h)
num_h=num_h+h(i).*lamda.^(length(h)-i);
end
num_g=0;
for i=1:1:length(g)
num_g=num_g+g(i).*lamda.^(length(g)-i);
end
num_f=(1-lamda.^2).^(n/2);
figure
plot(freq_solve/1e9,20*log10(abs(num_f./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S21)')
title('S21')
figure
plot(freq_solve/1e9,20*log10(abs(num_h./num_g)))
xlabel('Frequency(GHz)')
ylabel('dB(S11)')
title('S11')
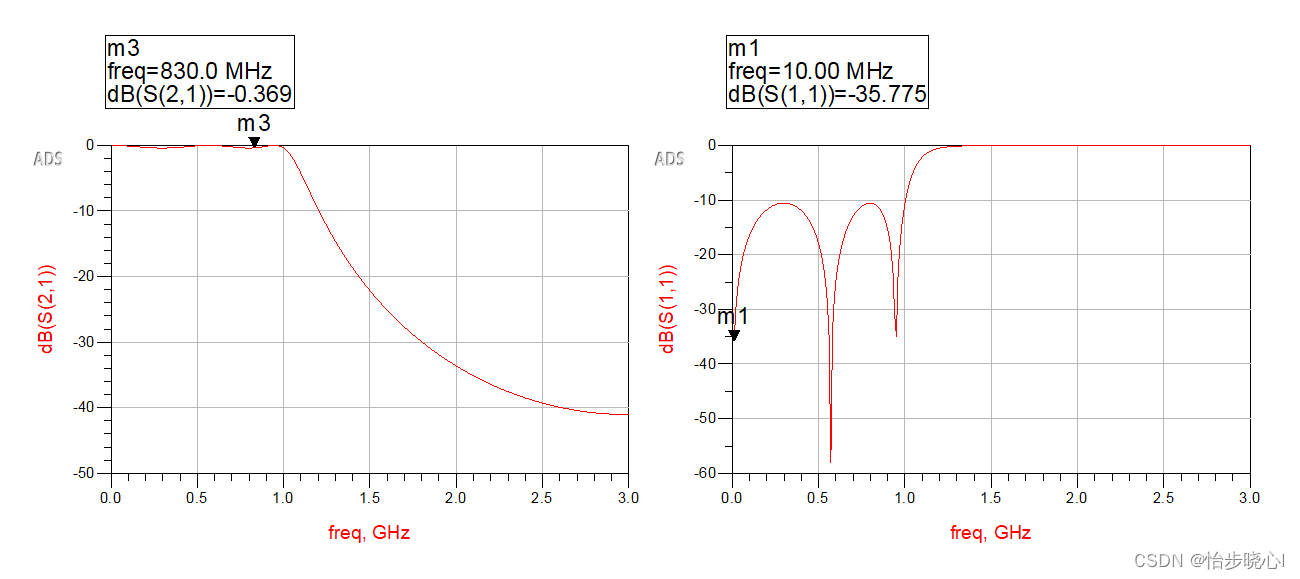
运行得到结果:
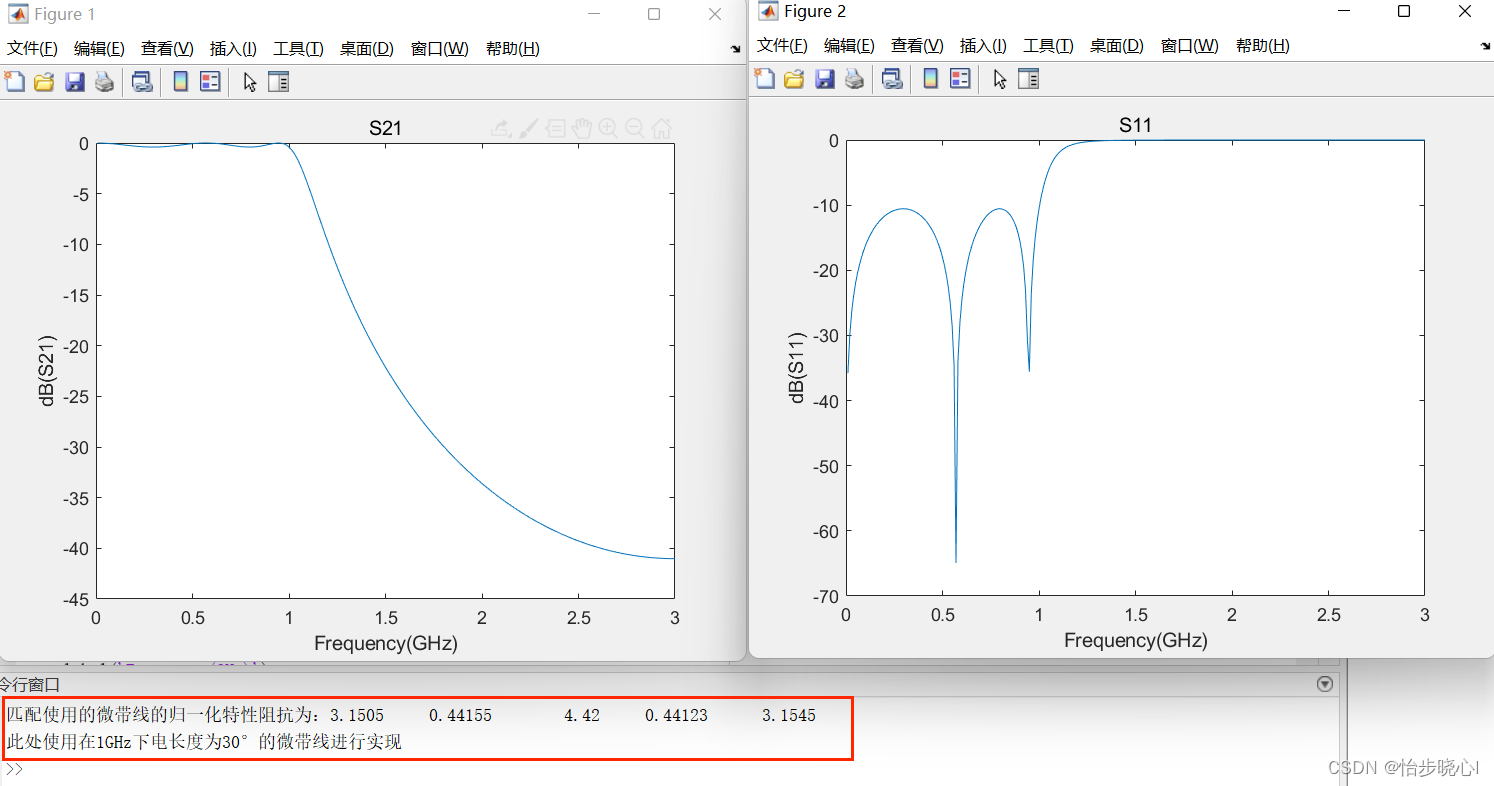
3、ADS验证
构建电路图:
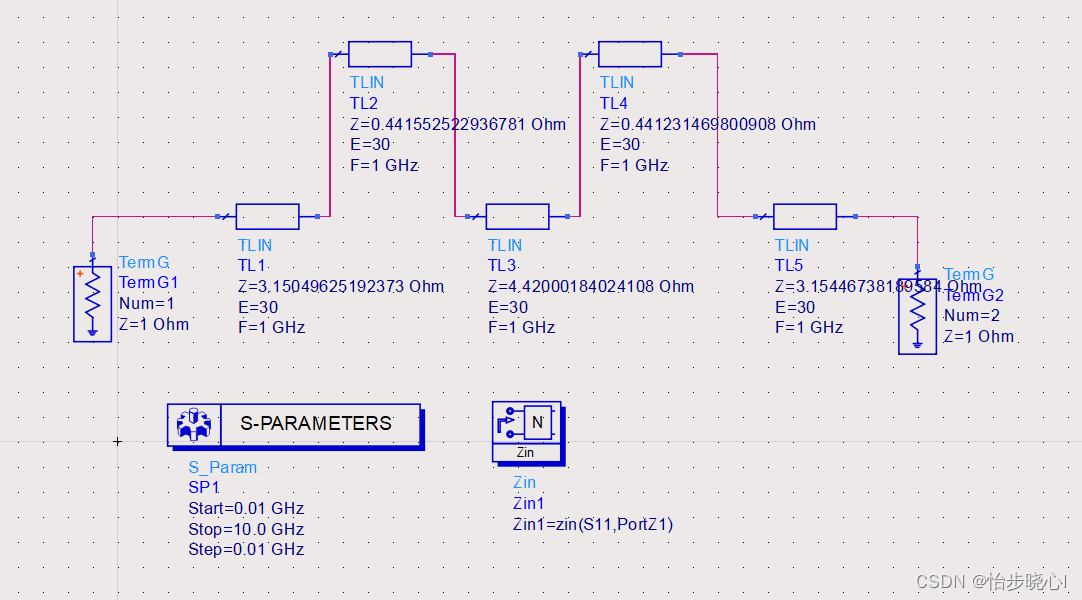
运行仿真,可见和理论结果一致(如果是50欧姆阻抗把所有数值都乘以50,也就是反归一化就行了):