递归算法
- 1199:全排列
- 1200:分解因数
- 1201:菲波那契数列
- 1202:Pell数列
- 1204:爬楼梯
- 1205:汉诺塔问题
1199:全排列

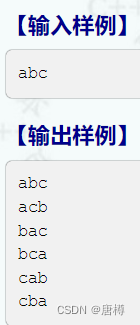
由题目可知,输入一个字符串,我们要对字符串进行所有可能的排序,但要注意,字符串要从小的字母到大的字母依次排。
这道题用深搜去做,会简单。
- 定义字符数组a存输入的字符串,字符数组b存储排列的字符。还有一个标记数组,用来标记这个字符串的字母有没有被用掉。
char a[10005],b[10005]; //a代表输入的字符串 b保持排列
bool f[10005]; //标记占有
int len;
- 主函数,输入值,先对字符串的第一个字母进行搜索排列。
int main(){
cin>>a;
len = strlen(a); //字符数组的长度获取
dfs(0); //0代表数组第一个位置
return 0;
}
- 从第一个到最后一个字符进行搜索,如果这个字符没有被用掉,则把这个字符值存到b数组,再标记已用掉。
void dfs(int t){
for(int i=0;i<len;i++){
if(f[a[i]]==0){ //没占有字符
f[a[i]] = 1;
b[t] = a[i]; //第t个位置保存字符
- 当搜索到最后一个字符,则输出我们的排列结果。没有搜索到最后一个的话,继续往下搜索。
if(t==len-1){
cout<<b<<endl;
}
else{
dfs(t+1);
}
f[a[i]] = 0;
}
}
}
完整代码:
#include<iostream>
#include<cstring>
using namespace std;
char a[10005],b[10005]; //a代表输入的字符串 b保持排列
bool f[10005]; //标记占有
int len;
//深搜模版1
void dfs(int t){
for(int i=0;i<len;i++){
if(f[a[i]]==0){ //没占有字符
f[a[i]] = 1;
b[t] = a[i]; //第t个位置保持
if(t==len-1){
cout<<b<<endl;
}
else{
dfs(t+1);
}
f[a[i]] = 0;
}
}
}
int main(){
cin>>a;
len = strlen(a); //字符数组的长度获取
dfs(0); //0代表数组第一个位置
return 0;
}
1200:分解因数

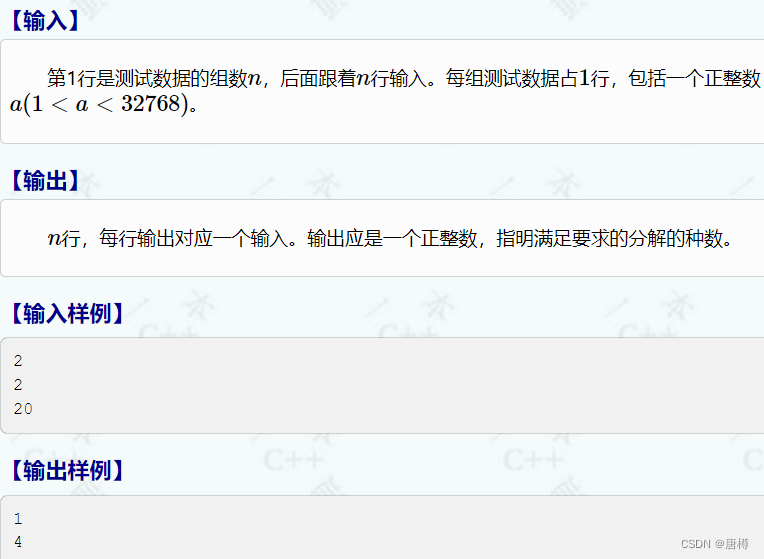
由题目可知,分解出来的数前面值要小于等于后面的数,自己本身也算一种分解。
- 20分解1:2 * 10
- 20分解2:2 * 2 * 5
- 20分解3:4 * 5
- 20分解4:20
20分解:5 * 4 (不满足 前小于后 的条件,不可分解!)
所以最终只有4种分解方式。
那我们开始做吧,首先搞定定义和输入。从这个数值,2开始分解,调用函数。
int main(){
cin>>n;
while(n--){
cin>>a; //对a分解
cnt=1; //自己本身也是一种分解方式
f(a,2); //a分解从2开始
cout<<cnt<<endl;
}
return 0;
}
- 函数结束条件,当求得的因子大于等于数值a,则结束!
void f(int a,int k){
if(k>=a) return ; //满足因子大于原值
- 从因子k开始循环到 最大因子 sqrt(a);保证 前小于后 的条件 循环判断 因子 i 能被整除也就是能分解,就次数+1;接着再调用函数继续分解剩下的值。
for(int i=k;i*i<=a;i++){ //从k开始分解
if(a%i==0){ //是因子
cnt++; //加1
f(a/i,i); //看继续分否
}
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
int n,a,cnt;
void f(int a,int k){
if(k>=a) return ; //满足因子大于原值
for(int i=k;i*i<=a;i++){ //从k开始分解
if(a%i==0){ //是因子
cnt++; //加1
f(a/i,i); //看继续分否
}
}
}
int main(){
cin>>n;
while(n--){
cin>>a; //对a分解
cnt=1; //自己本身也是一种分解方式
f(a,2); //a分解从2开始
cout<<cnt<<endl;
}
return 0;
}
1201:菲波那契数列
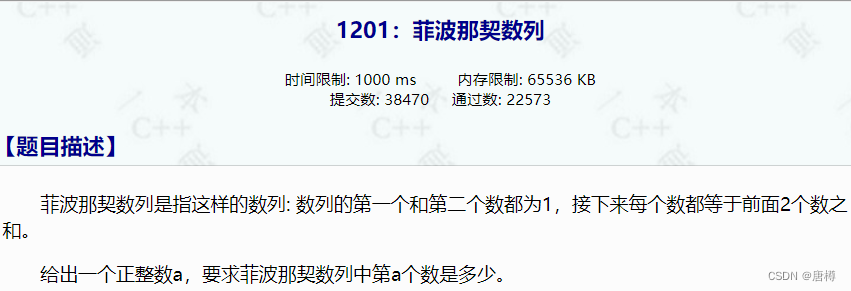
斐波那契数列很简单。递归边界条件,第一个值与第二个值都是1,递归式是前两个之和。
#include<bits/stdc++.h>
using namespace std;
long long f[22];
long long fbi(int n){
if(n==1 || n==2){
return f[n] = 1;
}
return f[n] = fbi(n-2)+fbi(n-1);
}
int main(){
int n,a;
cin>>n;
for(int i=1;i<=20;i++){
fbi(i);
}
for(int i=1;i<=n;i++){
cin>>a;
cout<<fbi(a)<<endl;
}
return 0;
}
1202:Pell数列

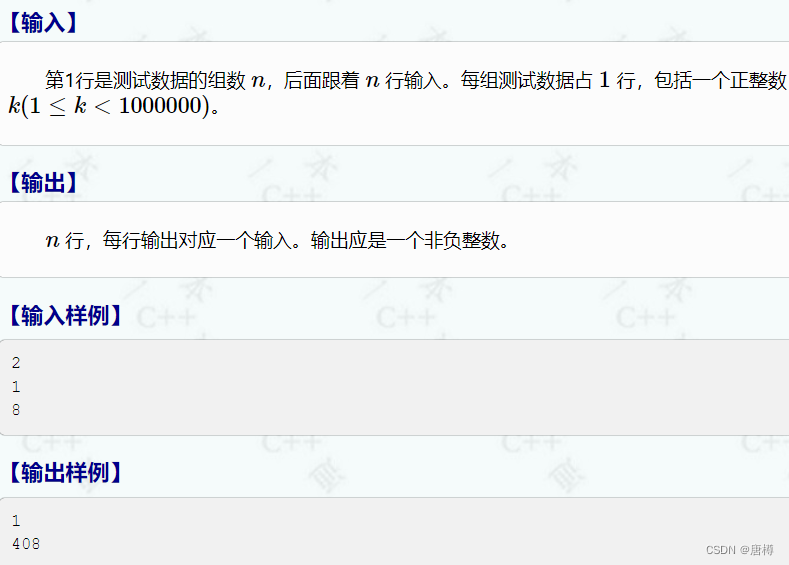
这个题也是类似斐波那契数列的,找到规律即可,第一项值1,第二项值2;这是递归边界。
- 先算出1到1000000的Pell数列值。
int main(){
int n,a;
for(int i=1;i<=1000000;i++){
pell(i); //函数调用求数列
}
- 根据输入求输出
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
cout<<f[a]<<endl;
}
- pell数列函数
long long f[1000009];
long long pell(int n){
if(f[n]!=0) return f[n];
if(n==1) return f[n]=1;
if(n==2) return f[n]=2;
return f[n] = (pell(n-1)*2+pell(n-2))%32767;
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
long long f[1000009];
long long pell(int n){
if(f[n]!=0) return f[n];
if(n==1) return f[n]=1;
if(n==2) return f[n]=2;
return f[n] = (pell(n-1)*2+pell(n-2))%32767;
}
int main(){
int n,a;
for(int i=1;i<=1000000;i++){
pell(i); //函数调用求数列
}
cin>>n;
for(int i=1;i<=n;i++){
cin>>a;
cout<<f[a]<<endl;
}
return 0;
}
1204:爬楼梯
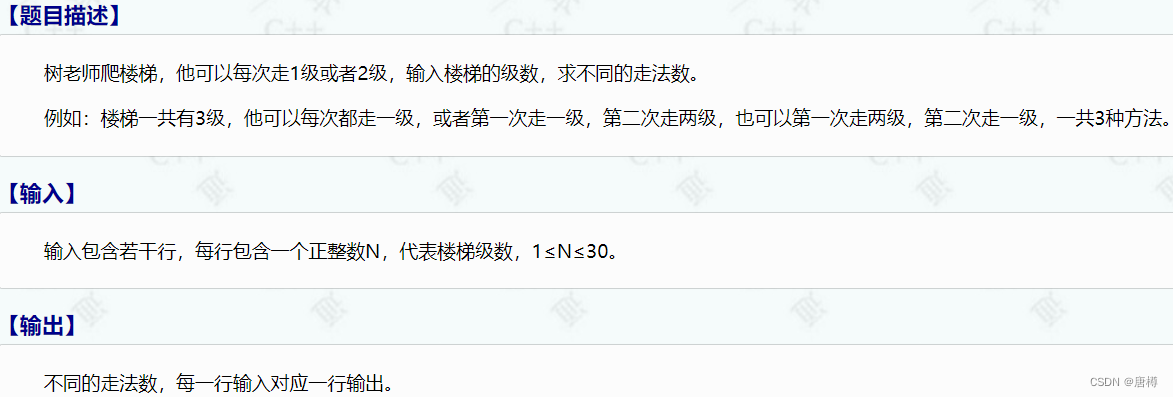
走楼梯问题,其实就是斐波那契数列问题。简单直接上代码
//1204:爬楼梯
#include<iostream>
using namespace std;
long long a[100],k;
long long pa(int n){
if(n==1) return a[1]=1;
if(n==2) return a[2]=2;
return a[n] = pa(n-1) + pa(n-2);
}
int main(){
while(cin>>k){
cout<<pa(k)<<endl;
}
return 0;
}
1205:汉诺塔问题
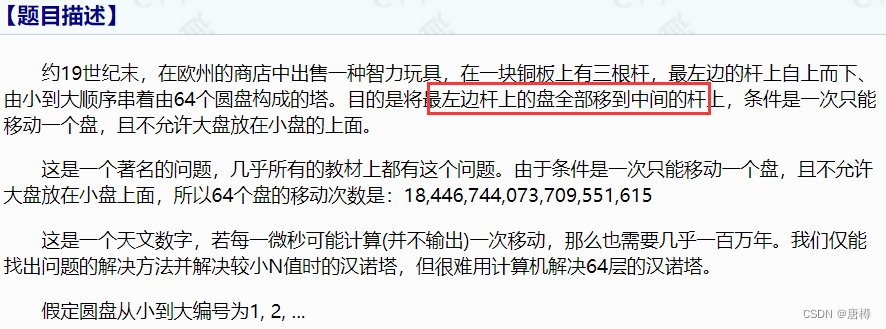
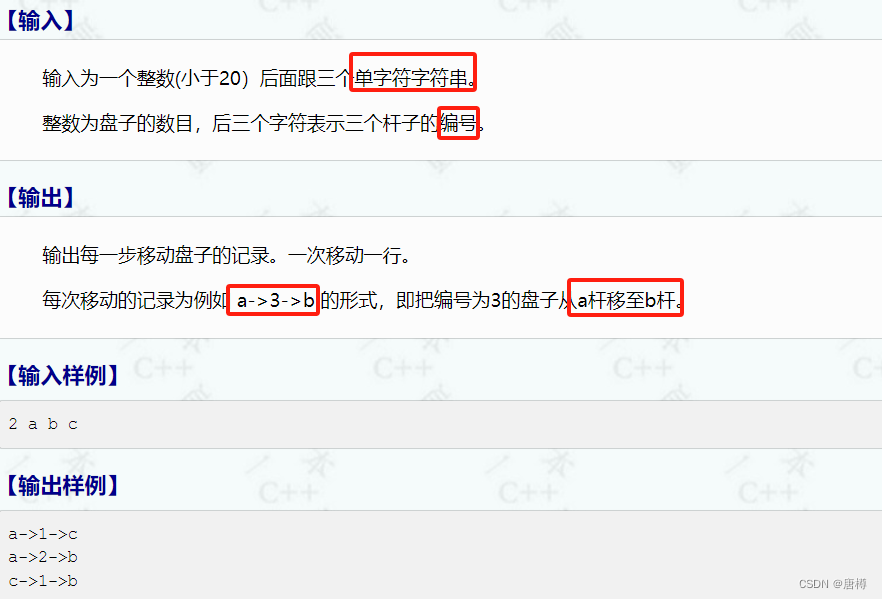
有题目可知,我们要把最左边的a杆盘子移到中间的b杆去。过程我们需要借助最右边的c杆。
假如有n个盘子,第n个盘子在最下面。那我们把上面的n-1个盘子都挪到 c 杆,这样是不是 a 杆只有一个最大盘子,可以挪到b杆了。最后把c杆的n-1个盘子挪到 b杆来。一直重复这样的动作就可以求出来的。
梳理成伪代码就是:输入搞定
int main(){
int n;
char a,b,c;
cin>>n>>a>>b>>c;
hanoi(n,a,b,c);
return 0;
}
- 开始按前面的规律步骤调用函数,如果 只有一个盘子就是输出移动结果。
void hanoi(int n,char a,char b,char c){ //初始,目的,经过
if(n==1){
// cout<<a<<"->"<<n<<"->"<<b<<endl;
printf("%c->%d->%c\n",a,n,b);
return;
}
- 第n个盘子上的n-1个盘子,挪动到c杆。也是就a杆到c杆,会经过b杆。
hanoi(n-1,a,c,b); //a到c,经过b
- 第n个盘子从a杆挪到b杆,直接输出移动过程
// cout<<a<<"->"<<n<<"->"<<b<<endl;
printf("%c->%d->%c\n",a,n,b);
- 剩下的n-1个盘子,从c杆到b杆,会经过a杆。
hanoi(n-1,c,b,a); //c到b,经过a
完整代码:
#include<bits/stdc++.h>
using namespace std;
void hanoi(int n,char a,char b,char c){ //初始,目的,经过
if(n==1){
// cout<<a<<"->"<<n<<"->"<<b<<endl;
printf("%c->%d->%c\n",a,n,b);
return;
}
hanoi(n-1,a,c,b); //a到c,经过b
// cout<<a<<"->"<<n<<"->"<<b<<endl;
printf("%c->%d->%c\n",a,n,b);
hanoi(n-1,c,b,a); //c到b,经过a
}
int main(){
int n;
char a,b,c;
cin>>n>>a>>b>>c;
hanoi(n,a,b,c);
return 0;
}