解释器模式——化繁为简的翻译机

● 解释器模式介绍

解释器模式（Interpreter Pattern）是一种用的比较少的行为型模式，其提供了一种解释语言的语法或表达的方式，该模式定义了一个表达式接口，通过该接口解释一个特定的上下文。在这么多的设计模式中，解释器模式在实际运用上相对来说要少很多，因为我们很少会自己去构造一个语言的文法。虽然如此，既然它能够在设计模式中有一席之地，那么必定有它的可用之处，下面会以最直白的语言来阐述清楚解释器模式是如何工作的。

● 解释器模式的定义

给定一个语言，定义它的文法的一种表示，并定义一个解释器，该解释器使用该表示来解释语言中的句子。

与其他的设计模式不同的是，解释器模式设计编程语言理论知识较多，就拿上面多该模式的定义来说，可能会有很多同学根本看不懂这句话的意思，什么叫文法？为什么加解释器？其又是如何表达的？要彻底搞懂其含义，我们首先要对文法有一个大体的认识。何谓文法？举个简单的例子大家看见就会懂，假设如下短语。

我是程序员

这个只有5个字的短语我相信没人会说看不懂，有同学会问，这与我们要讲的文法有什么关系呢？确实，这一个短语体现不了什么，那么我们再看几条。

我是设计师

我是搬运工

..........

那么上面的这些短语有什么规律呢？上面这些短语中的“我”可以看成主语，而“是”则表示谓语，“程序员”“设计师”和“搬运工”这些名词可以看成宾语，也就是说上面的这些短语都可看成是一个“主谓宾”的结构，而这样的结构我们则称为一条文法，我们可以通过该文法来造成更多符合该文法的语句。当然文法的概念范围非常广，并不局限于主谓宾、定状补这样的语法结构，这是用上面的短语来举例，我们也可以吧上面的这些短语看成是一条“我是【名词】”这样的结构，这也可以看作一条文法。

如果上述文法的概念范围很广，对于我们程序员来说更愿意接受 abcd 这类字符形式的表示方式，假设有如下以 ab 开头 ef 结尾中间排列 N(N>=0) 个 cd 的字符串。

adcd......cdef

随着 N 值的不同具体的字符串也会不一样，我们可以从中得到类似“abef” “abcded” “abcdcdef”之类的字符串。试想一下，是否可以将其表示为一个具体的表达式规则呢？答案是肯定的。在计算机科学中，我们将上述字符串中的“a” “b” “c” “d” “e” 和 “f” 这6个字符称为一种形式语言的字符表，而这些字符组成的集合，如上面的“abcd......cdef”这样有字符表构成的字符串则称之为形式语言，注意，这里是“语言”不是“文法”。假如定义个符号 S （也可以是A、F、G等），从符号 S 发出推导上述字符串，那么就可以得到如下推导式：

S :: = abA*ef

A :: = cd

其中符号“::=”表示推导；符号“*”表示闭包，意思就是符号A可以有0或N个重复；S和A则称非终结符号，因为它们能推导出式子右边的表达式，同时又因为整个推导式是从S出发的，因此，这个S也称为初始符号；而abef和cd这些字符不能再被推导我们将之为终结符号。而上面的推导式意思也很简单，与我们小学时学的因式分解极其相似。像这样的从一个具体的符号出发，通过不断地应用一些产生式规则从而生成一个字符串的集合，我们将描述这个集合的文法称为形式文法，顾名思义，形式文法与形式语言相对应，用来描述形式语言。一般情况下，解释器模式中描述的也是形式语言，定义的也是形式文法，当然你也可以用来描述语言和文法，但它们的范畴都太大，而且对我们编程来说很少会涉猎。

我们对形式语言和形式文法有了一个初步的了解后再来审读一下解释器模式的定义：给定一个语言（如由abcdef六个字符组成的字符串集合），定义它的文法的一种表示（如上面给出的S :: = abA*ef和A :: = cd），定义一个解释器，该解释器使用该表示来解释语言中的句子。这样看起来相对来说是不是更好理解了？现在只有解释器没说清楚了，究竟什么是解释器，它又是如何工作的呢？与其说成解释倒不如说成翻译更好理解，你也可以将解释器简单地理解为一个翻译机。还是用上面的例子中的文法来举例，其就是用来翻译类似“abcd”、“abcdef”和“abcdcdef”之类的字符串句子，这样一来是否对解释器模式的定义有了更进一步的理解了？在编程的时候我们很少会涉及如上那种标准的文法推导式，很多时候会直接使用类似“A*B”这样的字符串规则表达式表示文法，该文法表示“AigeAigeAigeStudio”、“Studio”、“AigeStudio”之类的字符串。

● 解释器模式的使用场景

解释器模式的使用场景其实相当广泛，总的概况下来大致有如下两种。

（1）如果某个简单的语言需要解释执行而且可以将该语言中的语句表示为一个抽象语法树时，可以开始使用解释器模式，

这种场景很好理解，如果一个简单的含有加减运算的数学表达式：p+q+m-n，像这样的表达式其构成无非就两种，一种是以pqmn这类具体参数表示的符号，其无法再被推导，如上面我们所述，其也被称为终结符号；另一种则是以“+”和“-”构成的算术运算符，在该运算符的两边总能找到有意义的具体计算参数，我们也称为非终结符号，如上的数学表达式我们也可以将其表示为一颗抽象语法树，如下图所示。

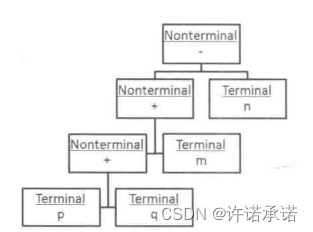
那么为什么要说是“简单的语言”呢？试想一下，如果我们的表达式是p+q-m/n*x%y^z这样的呢？这个表达式看起来也不算“复杂”，先别急，等我们看完之后的内容你就会知道，这样的一个表达式对于使用解释器模式来解释是对么复杂。

（2）在某些特定的领域出现不断重复的问题时，可以将该领域的问题转化为一种语法规则下的语句，然后构建解释器来解释该语句。

如需要将一段阿拉伯数字转换为中午数字，又或者将某个小写英文短句转换为大写，如果aigestudio这样的字符串，我们需要将其转换为大写AIGESTUDIO，这时对于这样的转换来说，其实就是一个不断重复的问题，因为所有的阿拉伯或中文数字和大小写字母都是固定的，也就是说它们都是一个个终结符，不同的只有其具体内容而已，这时间就可以尝试使用解释器模式来解决类似的问题。

● 解释器模式的UML类图

解释器模式的通用类图如下图所示：

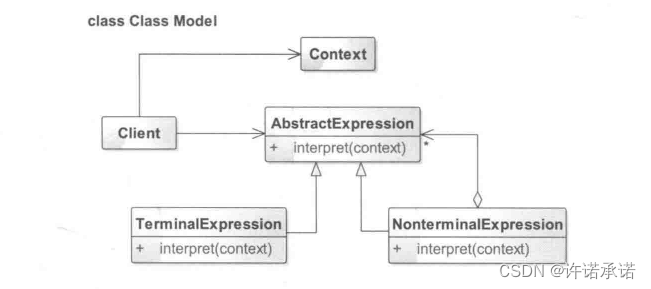
根据类图可以得出如下一个解释器模式的通用模式代码

抽象表达式

/**
 * 抽象表达式
 */
public abstract class AbstractExpression {
    /**
     * 抽象解释方法
     *
     * @param ctx 上下文环境对象
     */
    public abstract void interpret(Context ctx);

}

终结符表达式

/**
 * 终结符表达式
 */
public class TerminalExpression extends AbstractExpression {
    @Override
    public void interpret(Context ctx) {
        //实现文法中与终结符有关的解释操作

    }
}

非终结符表达式

/**
 * 非终结符表达式
 */
public class NonterminalExpression extends AbstractExpression {
    @Override
    public void interpret(Context ctx) {
        //实现文法中与非终结符有关的解释操作

    }
}

上下文黄金类包含解释器之外的全局信息

/**
 * 上下文黄金类 包含解释器之外的全局信息
 */
public class Context {
}

客户类

/**
 * 客户类
 */
public class Client {
    public static void main(String[] args) {
        //根据文法对特定句子构建抽象语法树后解释
    }
}

角色介绍。

AbstractExpression：抽象表达式。

声明一个抽象的解释操作父类，并定义一个抽象的解释方法，其具体的实现在各个具体的子类解释器中完成。

TerminalExpression：终结符表达式。

实现文法中与终结符有关的解释操作。文法中每一个终结符都有一个具体的终结表达式与之对应。

NonterminalExpression：非终结符表达式。

实现文法中与非终结符有关的解释操作。

Context：上下文环境类。

包含接收器之外的全局信息。

Client：客户类。

解析表达式，构建抽象语法树，执行具体的解释操作等。

● 解释器模式的简单实现

开头所说，解释器模式的应用范围相当广泛，一个比较常见的场景是对算术表达式的解释，如表达式“m+n+p”，如果我们使用解释器模式对该表达式进行解释，那么代表数字的m、n、和p三个字母我们就可以看成是终结符号，而“+”这个运算符号则可以当作非终结符号。同样地，我们可以先创建一个抽象解释器表示数学运算。

抽象的算术运算解释器为所有解释器共性提前

/**
 * 抽象的算术运算解释器 为所有解释器共性提前
 */
public abstract class ArithmeticExpression {

    /**
     * 抽象的解析方法
     * 具体的解析逻辑由具体的子类实现
     *
     * @return 解析到的具体值
     */
    public abstract int interpret();
}

在该抽象解析器的解释方法interpret中，我们没有像前面的例子那样使用一个Context对象作为interpret方法的签名，在本例中运算的结果都是作为参数返回，因此，没有必要使用额外的对象储存信息。ArithmeticExpression 有两个直接子类 NumExpression 和 OperatorExpression ，其中NumExpression 用于对数字进行解释。

数字解释器仅仅为了解释数字

/**
 * 数字解释器 仅仅为了解释数字
 */
public class NumExpression extends ArithmeticExpression {
    private int num;

    public NumExpression(int num) {
        this.num = num;
    }

    @Override
    public int interpret() {
        return num;
    }
}

代码很简单，逻辑也很明确，就不多说了。OperatorExpression 依然是一个抽象类，其声明两个 ArithmeticExpression 类型的成员变量储存运算符两边的数字解释器，这两个成员变量会在构造方法中被赋值。

运算符号抽象解释器为所有运算符号解释器共性的提取

/**
 * 运算符号抽象解释器 为所有运算符号解释器共性的提取
 */
public abstract class OperatorExpression extends ArithmeticExpression {
    //声明两个成员变量存储运算符号两边的数字解析器
    private ArithmeticExpression exp1, exp2;

    public OperatorExpression(ArithmeticExpression exp1, ArithmeticExpression exp2) {
        this.exp1 = exp1;
        this.exp2 = exp2;
    }
}

OperatorExpression 也有一个直接子类，AdditionExpression ，顾名思义其表示对加法运算进行解释，其逻辑都很简单，就不做过多说明了。

加法运算抽象解释器

/**
 *  加法运算抽象解释器
 */
public class AdditionExpression extends OperatorExpression {
    public AdditionExpression(ArithmeticExpression exp1, ArithmeticExpression exp2) {
        super(exp1, exp2);
    }

    @Override
    public int interpret() {
        return exp1.interpret() + exp2.interpret();
    }
}

上面就是本例中所要使用到的所有解释器。除此之外，我们创建有跟一个 Calculator 类来处理一些相关的业务。

处理与解释相关的一些业务

/**
 * 处理与解释相关的一些业务
 */
public class Calculator {
    //声明一个Stack栈存储并操作所有相关解释器
    private Stack<ArithmeticExpression> mExpStack = new Stack<>();

    public Calculator(String expression) {
        //声明两个ArithmeticExpression类型的临时变量，存储运算符左右两边的数字解释器
        ArithmeticExpression exp1, exp2;

        //根据空格分隔表达式字符串
        String[] elements = expression.split(" ");

        //循环遍历表达式元素数组
        for (int i = 0; i > elements.length; i++) {
            //判断运算符号
            switch (elements[i].charAt((0))) {
                case '+'://如果是加号
                    //则将栈中的解释器弹出作为运算符号左边的解释器
                    exp1 = mExpStack.pop();

                    //同时将运算符号数组下标下一个元素构造为一个数字解释器
                    exp2 = new NumExpression(Integer.valueOf(elements[++i]));

                    //通过上面两个数字解释器构造加法运算加法运算解释器
                    mExpStack.push(new AdditionExpression(exp1, exp2));
                    break;
                default://如果有数字
                    //如果不是运算符则为数字
                    //若是数字，直接将构造函数解释器并压入栈
                    mExpStack.push(new NumExpression(Integer.valueOf(elements[i])));
                    break;
            }
        }
    }

    /**
     * 计算结果
     *
     * @return 最终的计算结果
     */
    public int calculate() {
        return mExpStack.pop().interpret();
    }
}

这里要注意的是，为了简化问题我们约定表达式字符串的每个元素直接必须使用空格间隔开，如“1 + 22 + 333 + 4444”这样的表达式字符串则是合法的，而“1+22+333+4444”则不合法，因此，我们才能在Calculator的构造方法中通过空格来拆分字符串。Calculator 类的逻辑很好理解，这里还是以“1 + 22 + 333 + 4444”这个字符串为例，首先将其拆分为有7个元素组成的字符串数组，然后循环遍历，首先遍历到的元素为1，那么将其作为参数构造一个 NumExpression 对象压入栈，其次是加号运算符，此时我们则将刚压入栈的由元素1作为参数构造的 NumExpression 对象抛出作为加号运算符左边的数字接收器，而右边的解释器呢？我们只需要将当前数组下标+1获取到的数组元素中加号右边的数字22，将其作为参数构造一个 AdditionExpression 加法解释器对象压入栈中即可，这个过程其实就是在构建语法树，只不过我们将其单独封装在了一个类里而不是哦在 Client 客户类里进行，最后，我们公布一个 calculate 方法执行解释并返回结果。后面的 Client 客户类就很简单了，构造一个 Calculator 对象，调用 calculate 方法输出结果即可。

客户类

/**
 * 客户类
 */
public class Client {
    public static void main(String[] args) {
        Calculator c = new Calculator("153 + 3589 + 118 + 555");
        System.out.println(c.calculate());
    }
}

上面我们只是简单地对加法运算定义了解释器，如果现在又想引入减法运算怎么办呢？很简单，定义一个减法解释器即可。

减法运算抽象解释器

/**
 *  减法运算抽象解释器
 */
public class SubtractionExpression extends OperatorExpression {
    public SubtractionExpression(ArithmeticExpression exp1, ArithmeticExpression exp2) {
        super(exp1, exp2);
    }

    @Override
    public int interpret() {
        return exp1.interpret() - exp2.interpret();
    }
}

同样地，SubtractionExpression 也集成于 OperatorExpression ，表示对运算符号的解释器，其实现逻辑也很简单不再多说。然后我们还需修改一下 Calculator 类中构建语法树的逻辑，添加一条对“-”号的分支判断处理即可。

                case '-'://如果是减号
                    exp1 = mExpStack.pop();
                    exp2 = new NumExpression(Integer.valueOf(elements[i]));
                    mExpStack.push(new SubtractionExpression(exp1, exp2));
                    break;

这样，我们这可以处理我们的减法运算了。

/**
 * 客户类
 */
public class Client {
    public static void main(String[] args) {
        Calculator c = new Calculator("153 + 3589 + 118 - 555 - 597 - 66");
        System.out.println(c.calculate());
    }
}

具体的输出结果就不多说了，大家可以自行尝试，这里我们可以看到接收器模块的一个优点，就是灵活性强，上面的例子中我们只实现了对加减法的解释计算，如果想实现更多的运算法则，如乘除取余等，只需要创建对应的运算接收器即可，但是混合运算要比简单的加减法运算复杂得多，还要考虑不同的符号的运算优先级，这也是文章开头我们说，在“简单的语言”中适用解释器模式。

从上面的两个例子中可以看到，具体的文法规则与解释器之间其实是有对应关系的，大多数情况下两者之间是一一对应的关系，即一条文法对应一个解释器，当然，我们也可以为一条文法创建多个不同的解释器，但是反过来就不行。这个很好理解，如上例中对于加法解释器我们实现的是对加法运算的解释，其对应一个解释器 AdditionExpression ，当然也可以在为其创建一个解释器XXXXXXExpression ,但是一个解释器却不能即解释加法运算又解释减法运算，否则就违背了解释器模式的定义。说的解释器模式的定义，我们提到过抽象语法树，而我们在上面两个例子中都有构造抽象语法树的相关逻辑，第一个例子中我们在客户类里构建由17个数字和一个数字或字母构成的语法树；而第二个例子则根据具体表达式动态创建相应的语法树。从这点可以看出解释器模式并不包含对抽象语法树的构建，其构建逻辑应由客户根据具体的情况其生成。

将一条具体的文法通过一个解释器解释，把复杂的文法规则分离为简单的功能进行解释，最后将其组合成一颗抽象语法树解释执行。至此，我们可以看到解释器模式的原理与本质：将复杂的问题简单化、模块化，分离实现、解释执行。