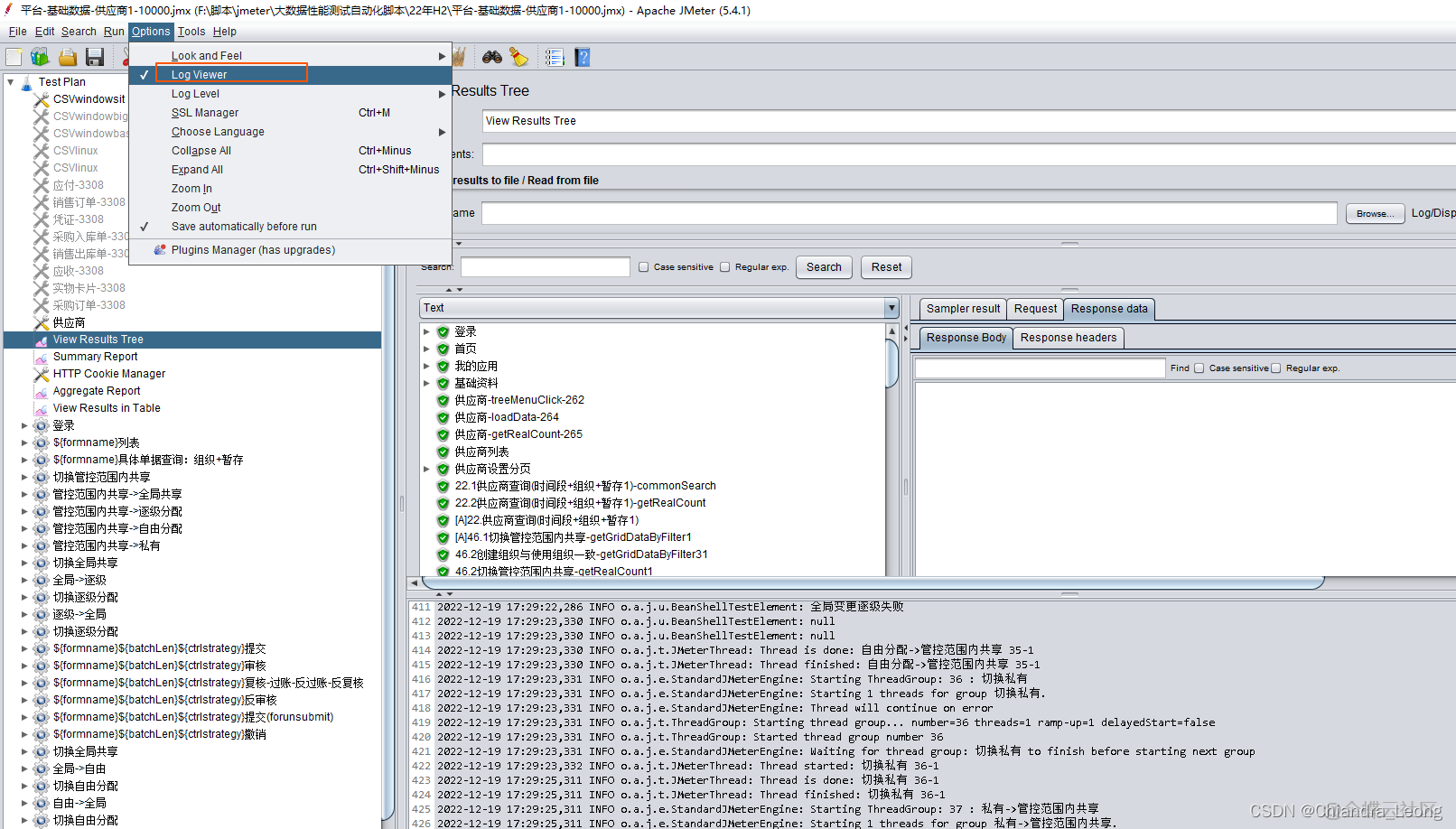
一些注意的点都在代码注释中了。

//有向图无环图中才有拓扑排序，且都是前面的编号的点指向后面编号的点
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 9;
int e[N], ne[N], h[N], idx, n, m, d[N], q[N];

void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool topsort()
{
	int hh = 0, tt = -1;
	//将所有入度为0的点入队，编号从1~n
	for (int i = 1; i <= n; ++i) if (!d[i]) q[++tt] = i;

	while (hh <= tt)
	{
		int t = q[hh++];//出队
		for (int i = h[t]; i != -1; i = ne[i])
		{
			int j = e[i];
			d[j]--;//因为t指向j，又因为t删除了，所以j入度减一
			if (!d[j]) q[++tt] = j;
		}
	}
	return tt == (n - 1);//如果每个点都入队了表明为拓扑排序
}

int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	memset(h, -1, sizeof h);
	cin >> n >> m;
	for (int i = 0; i < m; ++i)
	{
		int a, b; cin >> a >> b;
		add(a, b);
		d[b]++;//入度加一
	}
	//队列中的顺序刚好就是拓扑排序，排序不唯一
	if (topsort()) for (int i = 0; i < n; ++i) cout << q[i] << " ";
	else cout << -1;
	return 0;
}