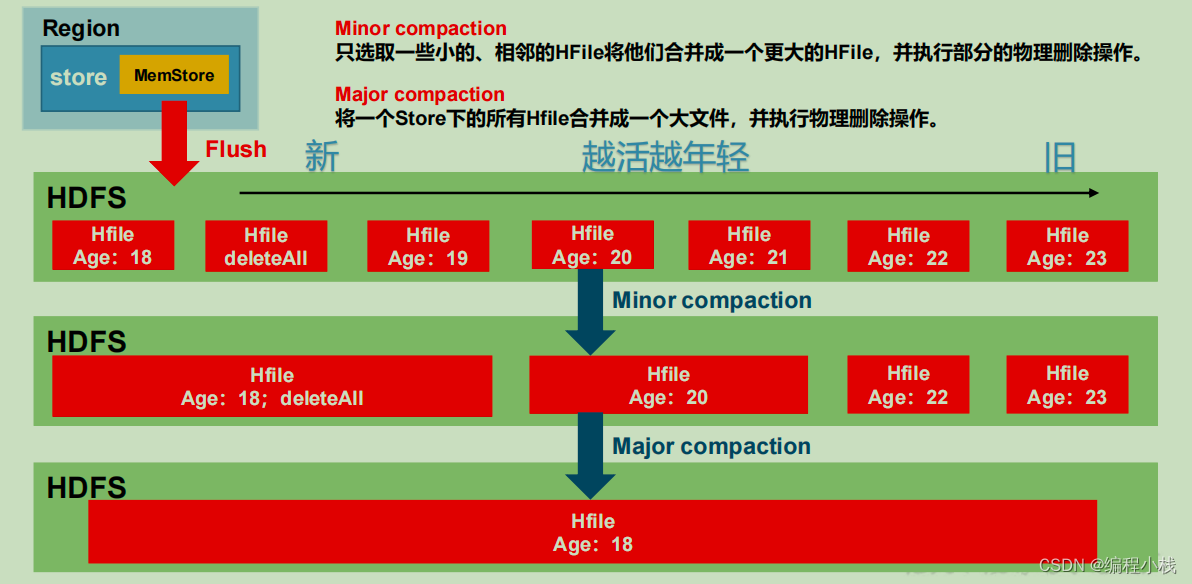
1.解码异或后的数组
未知 整数数组 arr 由 n 个非负整数组成。
经编码后变为长度为 n - 1 的另一个整数数组 encoded ,其中 encoded[i] = arr[i] XOR arr[i + 1] 。例如,arr = [1,0,2,1] 经编码后得到 encoded = [1,2,3] 。
给你编码后的数组 encoded 和原数组 arr 的第一个元素 first(arr[0])。
请解码返回原数组 arr 。可以证明答案存在并且是唯一的。
方法一:异或运算
#方法一:异或运算
def decode(encoded,first):
res=[0 for i in range(len(encoded)+1)]
res[0]=first
for i in range(1,len(encoded)+1):
res[i]=res[i-1]^encoded[i-1] #利用性质 encoded[i-1]=res[i]^res[i-1]
# encoded[i-1]^res[i-1]=res[i]
return res2.找出所有子集的异或总和再求和
一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果;如果数组为 空 ,则异或总和为 0 。
例如,数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。
给你一个数组 nums ,请你求出 nums 中每个 子集 的 异或总和 ,计算并返回这些值相加之 和 。
注意:在本题中,元素 相同 的不同子集应 多次 计数。
数组 a 是数组 b 的一个 子集 的前提条件是:从 b 删除几个(也可能不删除)元素能够得到 a 。

方法一:二进制枚举
#方法一:二进制枚举
def subsetXORSum(nums):
res=0
for i in range(0,1<<len(nums)):
tem=0
for j in range(0,len(nums)): #子集100表示取出第三个数 1100以此类推
if(i&(1<<j)):
tem^=nums[j] #二进制枚举,看这一位是不是1,是1就代表是子集元素
res+=tem
return res