递归算法
- 1206:放苹果
- 1207:求最大公约数问题
- 1208:2的幂次方表示
- 1209:分数求和
- 1210:因子分解
- 1211:判断元素是否存在
1206:放苹果
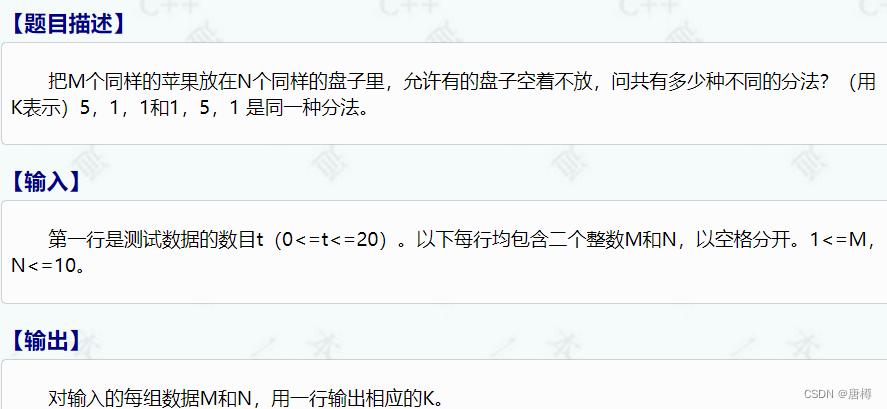
这道题还是有些难度的,我们要考虑几种放苹果的情况。我默默把m代表苹果,n代表盘子。
- 先把输入搞定,这个还是简简单单的。
int main(){
//多苹果,少盘子
// 例如f(4)(3) = f(4-3)(3) + f(4)(2);
// f(4)(2) = f(4-2)(2)+f(4)(1);
//测试数据次数
cin>>t;
for(int i=1;i<=t;i++){
int a,b;
cin>>a>>b; //输入每组数据
cout<<apple(a,b)<<endl;
}
return 0;
}
- 用apple函数求放苹果的次数。我们知道
多个苹果,0盘子; 多个苹果,1盘子;
0个苹果,多盘子;1个苹果,多盘子;
都只有一种方法哈。
if(m==0||m==1||n==0||n==1)
return f[m][n]=1;
-
第二种放苹果情况,就是 少苹果 多盘子,应该怎么放?
注意 题目讲道:
1 2 第一个盘子放1个苹果,第二个盘子放2个苹果;
2 1 第一个盘子放2个苹果,第二个盘子放1个苹果;
是一样的,只算一种方法。
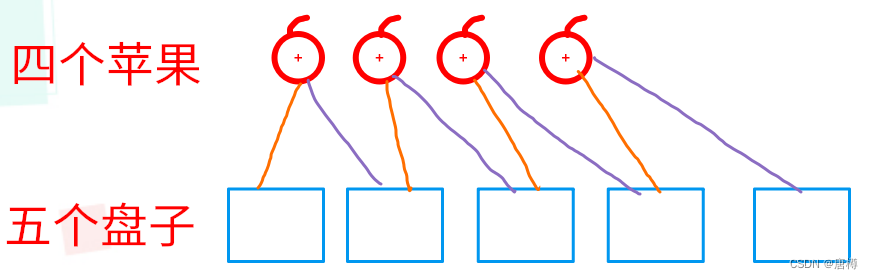
那上面图片:橙色线的放法 1 1 1 1 0 ;紫色线的放法 0 1 1 1 1 都算同一种; 4苹果🍎5盘子,其实就相当于 4苹果🍎4盘子的方法。代码表示则
return f[m][n] = apple(m,m);
- 最后一种情况:多苹果少盘子。
那这样,会出现每个盘子都至少有苹果🍎; 另外情况就是 有盘子没放苹果🍎; 把这两种可能加起来就是多苹果🍎少盘子的放法。
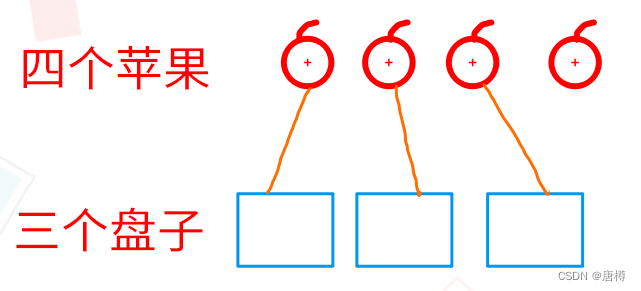
会出现每个盘子都至少有苹果🍎 那上面图片是不是有一个苹果没放对吧! 1个苹果3个盘子的放法是:
apple(4-3,3); //m苹果🍎,n盘子
apple(m-n,n);
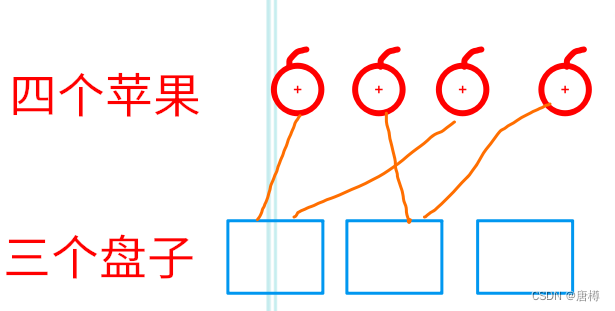
上图是有盘子没放苹果🍎的情况,则变成4个苹果🍎2个盘子的放法是:
apple(4,3-1); //m苹果🍎,n盘子
apple(m,n-1);
完整代码:
#include<bits/stdc++.h>
using namespace std;
int m,n,t; //m代表苹果,n代表盘子
int f[15][15]={0};
int apple(int m,int n){
// 多个苹果,0盘子; 多个苹果,1盘子;
// 0个苹果,多盘子;1个苹果,多盘子; 都只有一种
if(m==0||m==1||n==0||n==1) return f[m][n]=1;
if(m>=n){ //多苹果,少盘子
return f[m][n] = apple(m-n,n) + apple(m,n-1);
}
else{
return f[m][n] = apple(m,m);
}
}
int main(){
//多苹果,少盘子
// 例如f(4)(3) = f(4-3)(3) + f(4)(2);
// f(4)(2) = f(4-2)(2)+f(4)(1);
//测试数据次数
cin>>t;
for(int i=1;i<=t;i++){
int a,b;
cin>>a>>b; //输入每组数据
cout<<apple(a,b)<<endl;
}
return 0;
}
1207:求最大公约数问题
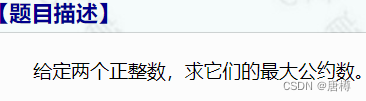
最大公约数用辗转相除法做即可。
#include<iostream>
using namespace std;
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
int a,b;
int main(){
cin>>a>>b;
cout<<gcd(a,b);
return 0;
}
1208:2的幂次方表示

- 输入一个值,这个值从0次方开始拆分
int main(){
int n;
cin>>n;
f(n,0);
return 0;
}
173 怎么得出2的几次方呢? 值n用短除法,不断➗2,有余数1代表次方有。除一次2,就次方k+1;直到n除到0结束。
void f(int n,int k){ //n是值,k是几方数
if(n==0) return ; //值0,结束
n /= 2;
f(n,k+1); //不断除2,往下搜
根据题目要求,分解要在余数为1的情况:
- 2的0次方分解: 2(0)
- 2的1次方分解: 2
- 2的2次方分解: 2(2)
- 2的2次方以上分解: 以次方k的值作为n,重新调用函数进行次方的再次分解。
if(yu==1){ //有余数,就输出
// cout<<"2("<<k<<")";
if(k==0) cout<<"2(0)";
else if(k==1) cout<<"2";
else if(k==2) cout<<"2(2)";
else{ //超过2的次方重新模拟调用
cout<<"2(";
f(k,0);//对7再进行模拟
cout<<")";
}
}
题目输出要有+号。注意当有余数和值不为0情况。
if(n!=0 && yu!=0) cout<<"+";
完整代码:
#include<bits/stdc++.h>
using namespace std;
void f(int n,int k){ //k是次方数
if(n==0) return ; //值0,结束
int yu = n % 2; //求余数
n /= 2;
f(n,k+1); //不断除2,往下搜
// 2进制数,哪个次方数是1、是0; 137= 010001001; 128+8+1
if(n!=0 && yu!=0) cout<<"+";
if(yu==1){ //有余数,就输出
// cout<<"2("<<k<<")";
if(k==0) cout<<"2(0)";
else if(k==1) cout<<"2";
else if(k==2) cout<<"2(2)";
else{ //超过2的次方重新模拟调用
cout<<"2(";
f(k,0);//对7再进行模拟
cout<<")";
}
}
}
int main(){
int n;
cin>>n;
f(n,0);
return 0;
}
1209:分数求和
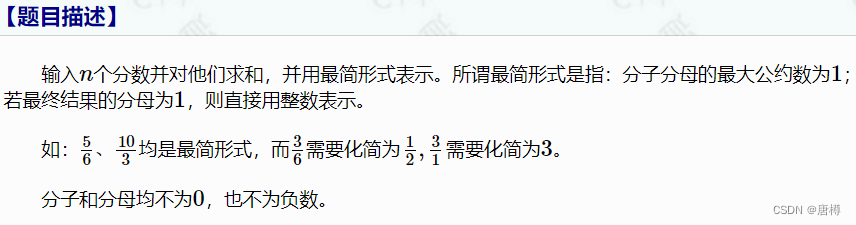

由题目可知,要模拟出分数相加的情况,也就是分母相乘,分子通分求和,在最后进行化简。
- 要定义变量,第一次输入值 表示第一个数的分子,分母。
int main(){
int a,b,n,fz,fm;
char c;
cin>>n;
cin>>a>>c>>b;
fz = a;
fm = b;
- 接着从第二个值的分数到第n个分数逐个输入,输入一个分数我们就进行通分操作。
for(int i=2;i<=n;i++){
cin>>a>>c>>b;
- 分子通分:
fz = fz*b + fm*a; //分子 - 分母相乘:
fm = fm*b; //分母
- 对通分的结果,进行最简化,那我们要同时分子分母除以最大的共同因子,也就是最大公约数。
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
int yue = gcd(fz,fm);
fz /= yue; //约分
fm /= yue; //约分
最后判断分母是1就直接输出分子。
if(fm==1) cout<<fz<<endl; //分母是1,直接输出分子
else cout<<fz<<"/"<<fm<<endl;
完整代码:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
int main(){
int a,b,n,fz,fm;
char c;
cin>>n;
cin>>a>>c>>b;
fz = a;
fm = b;
for(int i=2;i<=n;i++){
cin>>a>>c>>b;
fz = fz*b + fm*a; //分子
fm = fm*b; //分母
int yue = gcd(fz,fm);
fz /= yue; //约分
fm /= yue; //约分
}
if(fm==1) cout<<fz<<endl; //分母是1,直接输出分子
else cout<<fz<<"/"<<fm<<endl;
return 0;
}
1210:因子分解
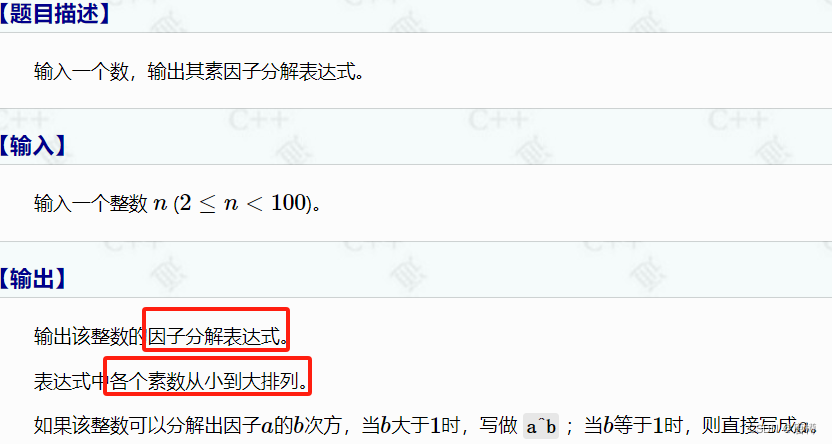
对n 从2到n进行除法,能被整除代表改因子可以分解。
int main(){
int n,cnt=0,f=0;
cin>>n;
for(int i=2;i<=n;i++){
//判断整除
}
如果能被整除,就统计这个因子 i 的次数 cnt+1。接着再对n进行分解,直到分解不了。
// 1.判断能被整除
if(n%i==0){
cnt = 0; //统计分解的次数
while(n%i==0){ //实现数字的分解
n = n/i;
cnt++;
}
再这个因子的次数有无超过1,有要输出 “^”;
乘号 * 输出在两个数中间。 最后判断n分解到值1就结束循环。
if(f==0) f=1; //保证乘号不能第一次
else cout<<"*";
cout<<i;
if(cnt>1) cout<<"^"<<cnt;
if(n==1) return 0;
完整代码
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,cnt=0,f=0;
cin>>n;
for(int i=2;i<=n;i++){
// 1.判断能被整除
if(n%i==0){
cnt = 0; //统计分解的次数
while(n%i==0){ //实现数字的分解
n = n/i;
cnt++;
}
if(f==0) f=1;
else cout<<"*";
cout<<i;
if(cnt>1) cout<<"^"<<cnt;
if(n==1) return 0;
}
}
return 0;
}
1211:判断元素是否存在
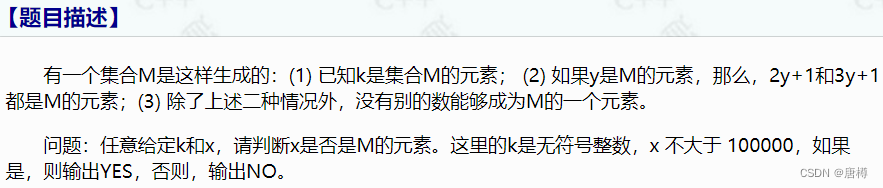

1.题目输入需要用到,c语言的输入方式。输入完判断是否满足条件,是就输出YES,否则NO。用函数去完成判断条件
int main(){
// cin>>k>>x;
scanf("%d,%d",&k,&x);
if(search(k)){
cout<<"YES";
}
else{
cout<<"NO";
}
return 0;
}
- x等于k也是满足函数条件,意味x是M的元素,因为k本身是M的元素
int x,k;
int search(int y){ //主函数k的值传到y
if(y==x){
return true;
}
当x<k是 不会满足2k+1和3k+1 的条件。
if(y>x){
return false;
}
当x>k是 调用下函数是否满足2k+1和3k+1 的条件。
if(x>y){
return search(2*y+1) || search(3*y+1);
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
int x,k;
int search(int y){
if(y==x){
return true;
}
if(y>x){
return false;
}
if(x>y){
return search(2*y+1) || search(3*y+1);
}
}
int main(){
// cin>>k>>x;
scanf("%d,%d",&k,&x);
if(search(k)){
cout<<"YES";
}
else{
cout<<"NO";
}
return 0;
}