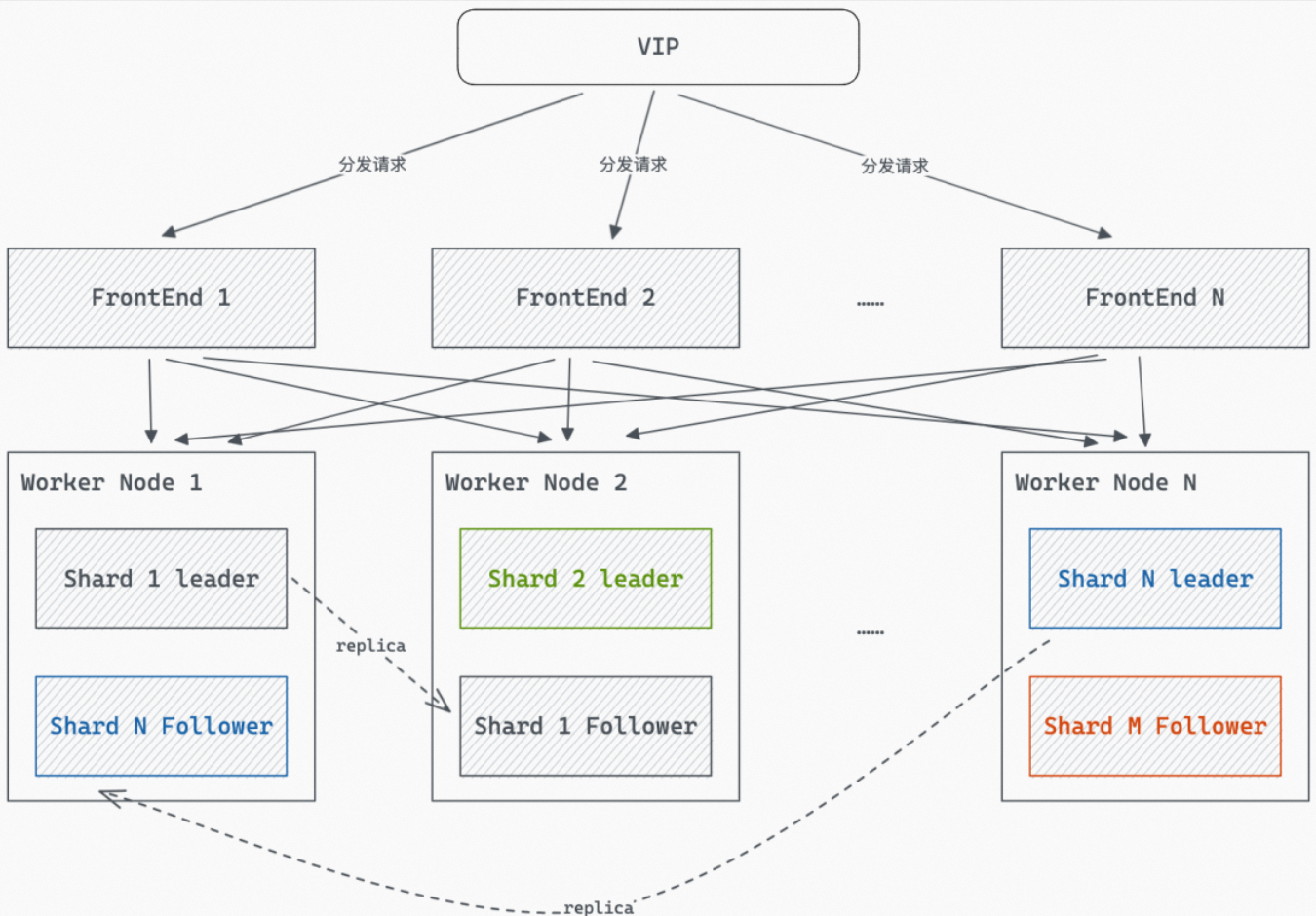
不同顺序欧拉角转旋转矩阵对照公式

eigen库求欧拉角公式

分别试验eigen库自带的matrix.eulerAngles()函数，与根据上述公式推导的两种方法求欧拉角
eigen库求得欧拉角的范围一定是$x->roll$方向在$[0,\pi ]$之间，$y->pitch$方向在$[-\pi ,\pi ]$之间，$z->yaw$方向在$[-\pi ,\pi ]$之间，优先会保证$x->roll$方向处于$[0,\pi ]$之间，才回去算别的角度。

以下代码验证：

#include <iostream>
#include <cmath>
#include <Eigen/Dense>

Quaterniond q(0.704,-0.708,0.05,0.002)//定义一个四元数;

Matrix3d m = q.toRotationMatrix();//四元数转旋转矩阵;

cout << q << endl;

cout << m << endl;

Quaterniond q1(m);//旋转矩阵转四元数，验证下四元数是否和原来输入的四元数一致

cout << q1 << endl;

cout << "XYZ------------" << endl;

Vector3d v=m.eulerAngles(0,1,2);//旋转矩阵转欧拉角，以XYZ为旋转方向

cout << v << endl;

cout << "ZYX------------" << endl;

Vector3d v1=m.eulerAngles(2,1,0);//旋转矩阵转欧拉角，以ZYX为旋转方向

cout << v1 << endl;

Vector3d v2;

输出的结果为

-0.708i + 0.05j + 0.002k + 0.704//四元数
 0.994992 -0.073616  0.067568
-0.067984 -0.002536  0.997064
-0.073232 -0.996664 -0.007528//旋转矩阵
-0.70756i + 0.049969j + 0.00199876k + 0.704437//四元数
XYZ------------//先转x
 1.56325//x roll
 3.07397//y pitch
-3.06774//z yaw
ZYX------------//先转z
3.07337// z yaw
3.06825//y pitch
1.56324//x roll

可以看到以上两种旋转顺序情况下用eigen库自带的matrix.eulerAngles()函数会使得z yaw，y pitch方向上计算的欧拉角数值增大，不利于机器人做角度控制，原本机器人可能朝反方向转很小的一个角度，可能现在需要转很大一圈。

用公式推导编写的代码：

//接着上面代码段补充运行即可
double sy=sqrt(m(0,0) * m(0,0) +  m(0,1) * m(0,1));
        if (sy>0.00001)//判断万向锁奇异
        {
            v2(0) = std::atan2(-m(1, 2), m(2, 2));
            v2(1) = std::atan2(m(0, 2), sy);
            v2(2) = std::atan2(-m(0, 1), m(0, 0));
        }
        else//奇异
        {
            v2(0) = 0;
            v2(1) = std::atan2(m(0, 2), sy);
            v2(2) = std::atan2(-m(1, 0), m(2, 0));
        }
cout << "XYZ------------" << endl;
cout << v2 << endl;
        if (sy>0.00001)//判断万向锁奇异
        {
            v2(0) = std::atan2(m(2, 1), m(2, 2));
            v2(1) = std::atan2(m(2, 0), sy);
            v2(2) = std::atan2(-m(1, 0), m(0, 0));
        }
        else//奇异
        {
            v2(0) = std::atan2(-m(1, 2), m(1, 1));;
            v2(1) = std::atan2(m(2, 0), sy);
            v2(2) = 0;
        }
cout << "ZYX------------" << endl;
cout << v2 << endl;

输出结果：

XYZ------------
 -1.57835//x
0.0676197//y
 0.073852//z
ZYX------------
  -1.57835  //注意这里还是x，与`eigen`库自带的`matrix.eulerAngles()`出来的顺序不一样
-0.0732686
 0.0682201//注意这里还是z

这里角度明显小很多，两种不同的方法的结果可以通过加减π得到，但是XYZ、ZYX两种不同顺序下的结果还不一样

因此建议直接用公式推导出来的方法。

参考:
https://zhuanlan.zhihu.com/p/85108850
https://blog.csdn.net/u011906844/article/details/121863578
https://blog.csdn.net/zhuoqingjoking97298/article/details/122259409
https://blog.csdn.net/WillWinston/article/details/125746107